ПРИЗМЫ

I уровень

1.1. Диагональ правильной четырехугольной призмы равна 25 см, а диагональ ее боковой грани – 20 см. Найдите высоту призмы.

1.2. Сечение железнодорожной насыпи имеет вид трапеции, нижнее основание которой 14 м, верхнее 8 м и высота 3,2 м. Определите, сколько кубических метров земли приходится на 1 км насыпи.

1.3. В наклонной треугольной призме проведено сечение, перпендикулярное боковому ребру, равному 12 см. В полученном треугольнике две стороны с длинами см и 8 см образуют угол 45. Найдите площадь боковой поверхности призмы.

1.4. Основанием прямого параллелепипеда является ромб со стороной 4 см и острым углом 60. Найдите диагонали параллелепипеда, если длина бокового ребра равна 10 см.

1.5. Основанием прямого параллелепипеда является квадрат с диагональю, равной см. Боковое ребро параллелепипеда 5 см. Найдите площадь полной поверхности параллелепипеда.

1.6. Основанием наклонного параллелепипеда является прямоугольник со сторонами 3 см и 4 см. Боковое ребро, равное  см, наклонено к плоскости основания под углом 60. Найдите объем параллелепипеда.

1.7. Вычислите площадь поверхности прямоугольного параллелепипеда, если два ребра и диагональ, исходящие из одной вершины, равны соответственно 11 см, см и 13 см.

1.8. Определите вес каменной колонны, имеющей форму прямоугольного параллелепипеда, с размерами 0,3 м, 0,3 м и 2,5 м, если удельный вес материала равен 2,2 г/см³.

1.9. Найдите площадь диагонального сечения куба, если диагональ его грани равна дм.

1.10. Найдите объем куба, если расстояние между двумя его вершинами, не лежащими в одной грани, равно см.

II уровень

2.1. Основанием наклонной призмы является равносторонний треугольник со стороной 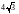см. Боковое ребро наклонено к плоскости основания под углом 30. Найдите площадь сечения призмы, проходящего через боковое ребро и высоту призмы, если известно, что одна из вершин верхнего основания проектируется на середину стороны нижнего основания.

2.2. Основанием наклонной призмы является равносторонний треугольник ABC со стороной, равной 3 см. Вершина A₁ проектируется в центр треугольника ABC. Ребро AA₁ составляет с плоскостью основания угол 45. Найдите площадь боковой поверхности призмы.

2.3. Вычислите объем наклонной треугольной призмы, если стороны основания 7 см, 5 см и 8 см, а высота призмы равна меньшей высоте треугольника-основания.

2.4. Диагональ правильной четырехугольной призмы наклонена к боковой грани под углом 30. Найдите угол наклона к плоскости основания.

2.5. Основанием прямой призмы является равнобедренная трапеция, основания которой равны 4 см и 14 см, а диагональ – 15 см. Две боковые грани призмы – квадраты. Найдите площадь полной поверхности призмы.

2.6. Диагонали правильной шестиугольной призмы равны 19 см и 21 см. Найдите ее объем.

2.7. Найдите измерения прямоугольного параллелепипеда, у которого диагональ равна 8 дм, и она образует с боковыми гранями углы 30 и 40.

2.8. Диагонали основания прямого параллелепипеда равны 34 см и 38 см, а площади боковых граней – 800 см² и 1200 см². Найдите объем параллелепипеда.

2.9. Определите объем прямоугольного параллелепипеда, в котором диагонали боковых граней, выходящие из одной вершины, равны 4 см и 5 см и образуют угол 60.

2.10. Найдите объем куба, если расстояние от его диагонали до непересекающегося с ней ребра равно мм.