
Лабораторная работа 4 / LR_4 / ВМ_4
.docМинистерство образования и науки РФ
Санкт-Петербургский государственный электротехнический университет
“ЛЭТИ”
кафедра МОЭВМ
Лабораторная работа №4 по дисциплине вычислительная математика
на тему:
«Метод хорд».
г. Санкт-Петербург
-
Год
I. Цель работы:
Найти корень уравнения
![]() для функции
для функции
![]() методом хорд с заданной точностью
Eps, исследовать скорость
сходимости и обусловленности метода.
методом хорд с заданной точностью
Eps, исследовать скорость
сходимости и обусловленности метода.
II. Общие сведения:
Пусть
найден отрезок [a,
b],
на котором функция
![]() меняет
знак. Для определенности положим
меняет
знак. Для определенности положим
![]() (a)>0,
(a)>0,
![]() (b)<0.
В методе хорд процесс итераций состоит
в том, что в качестве приближений к корню
уравнения
(b)<0.
В методе хорд процесс итераций состоит
в том, что в качестве приближений к корню
уравнения
![]() принимаются значения c0,
c1,
. . . точек пересечения хорды с осью
абсцисс, как это показано на рис.1.
принимаются значения c0,
c1,
. . . точек пересечения хорды с осью
абсцисс, как это показано на рис.1.
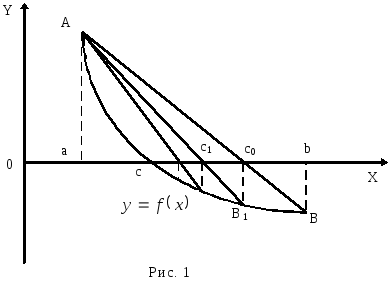
Сначала находится уравнение хорды АВ:
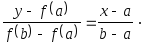
Для точки пересечения ее с осью абсцисс (x=c0, y=0) получается уравнение
![]()
Далее
сравниваются знаки величин
![]() (a)
и
(a)
и
![]() (с0)
и для рассматриваемого случая оказывается,
что корень находится в интервале (a,
c0),
так как
(с0)
и для рассматриваемого случая оказывается,
что корень находится в интервале (a,
c0),
так как
![]() (a)
*
(a)
*![]() (с0)<0.
Отрезок [c0,b]
отбрасывается. Следующая итерации
состоит в определении нового приближения
c1
как точки пересечения хорды АВ1
с осью абсцисс и т.д. Итерационный процесс
продолжается до тех пор, пока значение
(с0)<0.
Отрезок [c0,b]
отбрасывается. Следующая итерации
состоит в определении нового приближения
c1
как точки пересечения хорды АВ1
с осью абсцисс и т.д. Итерационный процесс
продолжается до тех пор, пока значение
![]() (cn)
не станет по модулю меньше заданного
числа .
(cn)
не станет по модулю меньше заданного
числа .
Алгоритмы методов бисекции и хорд похожи, однако метод хорд в ряде случаев дает более быструю сходимость итерационного процесса, причем успех его применения, как и метода бисекции, гарантирован.
III. Порядок выполнения работы:
-
Графически или аналитически отделить корень уравнения
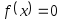 (т.е. найти отрезки [Left,
Right],
на которых функция
(т.е. найти отрезки [Left,
Right],
на которых функция
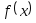 удовлетворяет
условиям применимости метода).
удовлетворяет
условиям применимости метода). -
Составить подпрограмму - функцию вычисления функции
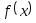 ,
предусмотрев округление значений
функции с заданной точностью Delta
с использованием программы Round.
,
предусмотрев округление значений
функции с заданной точностью Delta
с использованием программы Round. -
Составить головную программу, вычисляющую корень уравнения
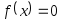 и
содержащую обращение к подпрограмме
f(x),
HORDA,
Round
и индикацию результатов.
и
содержащую обращение к подпрограмме
f(x),
HORDA,
Round
и индикацию результатов. -
Провести вычисления по программе. Теоретически и экспериментально исследовать скорость сходимости и обусловленность метода.
IV. Выполнение работы:
-
Отделим графическим методом корни уравнения
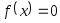 ,
т.е. найдем отрезки
,
т.е. найдем отрезки

![]() удовлетворяет
условиям применимости метода бисекции.
Для этого сначала определим абсолютное
число обусловленности задачи вычисления
корня:
удовлетворяет
условиям применимости метода бисекции.
Для этого сначала определим абсолютное
число обусловленности задачи вычисления
корня:
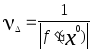 =
,
=
,
тогда Eps ≤ Delta / |1/(3x2-3+2e-x) |.
Теперь графически определим отрезок [Left, Right].
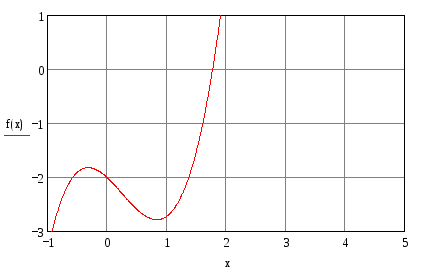
Где
![]() .
.
Проанализировав результаты, мы получаем отрезок [1, 2].
2)
Составим подпрограмму - функцию вычисления
функции
![]() ,
предусмотрев округление значений
функции с заданной точностью Delta
с использованием программы Round.
,
предусмотрев округление значений
функции с заданной точностью Delta
с использованием программы Round.
double F(double x)
{
extern double c,d,delta;
double s;
long int S;
s = x*x*x-3*x-2*exp(-x);
if( s/delta < 0 )
S = s/delta - .5;
else
S = s/delta + .5;
s = S*delta;
s = Round( s,delta );
return(s);
}
3)
Составим головную программу, вычисляющую
корень уравнения
![]() и
содержащую обращение к подпрограмме
f(x),
HORDA,
Round
и индикацию результатов.
и
содержащую обращение к подпрограмме
f(x),
HORDA,
Round
и индикацию результатов.
void main()
{
clrscr();
int k;
long int s;
float a1,b1,eps1,delta1;
double a,b,eps,x;
double F(double);
cout<<"f(x)=x*x*x-3x-2e(deg(-x))"<<endl<<endl;
printf("Input eps: ");
scanf("%f",&eps1);
eps = eps1;
printf("Input a: ");
scanf("%f",&a1);
a = a1;
printf("Input b: ");
scanf("%f",&b1);
b = b1;
printf("Input delta: ");
scanf("%f",&delta1);
delta = delta1;
x = HORDA(a,b,eps,k);
printf("x=%f k=%d\n",x,k);
getch();
}
4) Проведем вычисления по программе, варьируя значения параметров Eps (точность вычисления корня) и Delta (точность задания исходных данных).
|
eps |
delta |
a |
b |
x* |
k |
|
0,1 |
0,1 |
1 |
2 |
1,782341 |
2 |
|
0,01 |
0,1 |
1 |
2 |
1,782341 |
2 |
|
0,001 |
0,1 |
1 |
2 |
1,782341 |
2 |
|
0,0001 |
0,1 |
1 |
2 |
1,782341 |
2 |
|
0,00001 |
0,1 |
1 |
2 |
1,782341 |
2 |
|
0,000001 |
0,1 |
1 |
2 |
1,782341 |
2 |
|
0,1 |
0,01 |
1 |
2 |
1,781064 |
3 |
|
0,01 |
0,01 |
1 |
2 |
1,784796 |
3 |
|
0,001 |
0,01 |
1 |
2 |
1,784796 |
3 |
|
0,0001 |
0,01 |
1 |
2 |
1,784796 |
3 |
|
0,00001 |
0,01 |
1 |
2 |
1,784796 |
3 |
|
0,000001 |
0,01 |
1 |
2 |
1,784796 |
3 |
|
0,1 |
0,001 |
1 |
2 |
1,781506 |
3 |
|
0,01 |
0,001 |
1 |
2 |
1,784866 |
4 |
|
0,001 |
0,001 |
1 |
2 |
1,785486 |
5 |
|
0,0001 |
0,001 |
1 |
2 |
1,785486 |
5 |
|
0,00001 |
0,001 |
1 |
2 |
1,785486 |
5 |
|
0,000001 |
0,001 |
1 |
2 |
1,785486 |
5 |
|
0,1 |
0,0001 |
1 |
2 |
1,781510 |
3 |
|
0,01 |
0,0001 |
1 |
2 |
1,784893 |
4 |
|
0,001 |
0,0001 |
1 |
2 |
1,785377 |
5 |
|
0,0001 |
0,0001 |
1 |
2 |
1,785464 |
6 |
|
0,00001 |
0,0001 |
1 |
2 |
1,785464 |
6 |
|
0,000001 |
0,0001 |
1 |
2 |
1,785464 |
6 |
|
0,1 |
0,00001 |
1 |
2 |
1,781505 |
3 |
|
0,01 |
0,00001 |
1 |
2 |
1,784890 |
4 |
|
0,001 |
0,00001 |
1 |
2 |
1,785379 |
5 |
|
0,0001 |
0,00001 |
1 |
2 |
1,785449 |
6 |
|
0,00001 |
0,00001 |
1 |
2 |
1,785462 |
7 |
|
0,000001 |
0,00001 |
1 |
2 |
1,785462 |
7 |
|
0,1 |
0,000001 |
1 |
2 |
1,781505 |
3 |
|
0,01 |
0,000001 |
1 |
2 |
1,784890 |
4 |
|
0,001 |
0,000001 |
1 |
2 |
1,785379 |
5 |
|
0,0001 |
0,000001 |
1 |
2 |
1,785450 |
6 |
|
0,00001 |
0,000001 |
1 |
2 |
1,785461 |
8 |
|
0,000001 |
0,000001 |
1 |
2 |
1,785461 |
8 |
-
delta=0.1: b) delta=0.01:

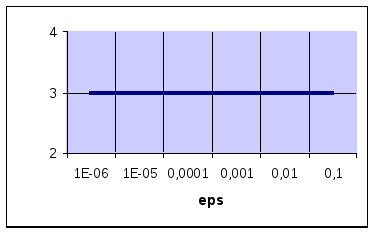
-
delta=0.001: d) delta=0.0001:
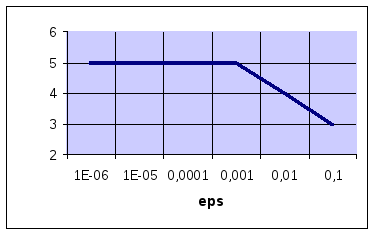
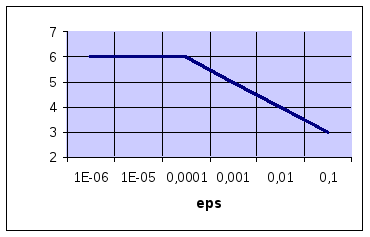
e) delta=0.00001: f) delta=0.000001:
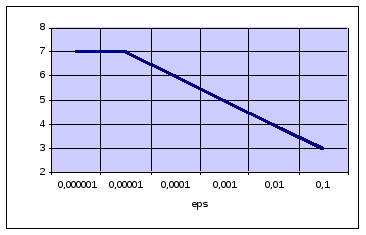
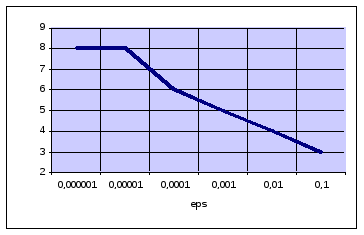
5) Из полученных результатов видно, что, чем более высокая точность выходных данных нам необходима, тем больше нам необходимо сделать итераций. Кроме того, из таблицы видно, что с ростом ошибок в исходных данных, уменьшается точность выходных данных. Таким образом, теоретические результаты совпадают с экспериментальными данными.
V. Вывод:
Проанализировав результаты работы
программы, мы можем сделать вывод, что
число итераций метода хорд возрастает
с ростом требуемой точности выходных
данных. Обусловленность задачи нахождения
корня уравнения
![]() для функции
для функции
![]() прямо пропорциональна величине
|1/(3x2-3+2e-x)|
и точности задания исходных данных и
обратно пропорциональна точности
вычисления корня, т. е., чем ближе
|1/(3x2-3+2e-x)
| и Delta к 0 и чем больше
Eps, тем задача хуже
обусловлена, и наоборот.
прямо пропорциональна величине
|1/(3x2-3+2e-x)|
и точности задания исходных данных и
обратно пропорциональна точности
вычисления корня, т. е., чем ближе
|1/(3x2-3+2e-x)
| и Delta к 0 и чем больше
Eps, тем задача хуже
обусловлена, и наоборот.
