
- •Хабаровская государственная академия экономики и права
- •Дойхен Людмила Архиповна
- •Подписано в печать . Формат . Бумага писчая.
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 29
- •Вариант 30
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
Вариант 4
 ;
; 9.
9.
 ;
;
 ;
10.
;
10.
 ;
;
 ;
11.
;
11.
 ;
;
 ;
12.
;
12.
 ;
;
 ;
13.
;
13.
 ;
;
 ;
14
;
14 ;
;
 ;
15.
;
15.
 ;
;
 ;
16.
;
16.
 .
.
Вычислить площадь фигуры, ограниченной следующими линиями:
а) y=x2-1, y=3;
б) y=(x-4)2 и y=16-x2;
в) y2=4x, xy=2, x=4.
Определить дневную выработку рабочего за шестичасовой рабочий день, если производительность труда y в течение дня меняется по закону y=y0(-0,5t2 + 0,6t +1,2), где y0-максимальная производительность рабочего, t- время в часах от начала смены.
Вариант 5
 ;
9.
;
9.
 ;
;
 ;
10.
;
10.
 ;
;
 ;
11.
;
11.
 ;
;
 ;
12.
;
12.
 ;
;
 ;
13.
;
13.
 ;
;
 ;
14.
;
14.
 -x
-x
 ;
;
 ;
15.
;
15.
 ;
;
; 16.
 .
.
Вычислить площадь фигуры, ограниченной линиями:
а)
 и
и
 ;
;
б)
 ,
,
 ,
,
 ;
;
в)
 ,
,
 ,
.
,
.
18.
Определить объем, выпущенной продукции
до перерыва, т.е. для промежутка [ 0; 3] и
после перерыва, т.е. для промежутка [3;
6], если производительность
 ,
где
,
где
 -
максимальная производительность, t
– время в часах.
-
максимальная производительность, t
– время в часах.
Вариант 6
 ;
9.
;
9.
 ;
;
 ;
10.
;
10.
 ;
;
 ;
11.
;
11.
 ;
;
 ;
12.
;
12.
 ;
;
 ;
13.
;
13.
 ;
;
 ;
14.
;
14.
 ;
;
 ;
15.
;
15.
 ;
;
 ;
16.
;
16.
 .
.
17. Вычислить площадь фигуры, ограниченной линиями:
а) y=12+6x-x2, y=x2-2x+2;
б) xy=-9, x-y-10=0;
в)
y=
cosx
и осью ОХ на 0x .
.
18.
Тариф перевозки 1 тонны груза составляет
y
руб/км и
убывает с ростом пройденного
расстояния x
(в км) по
закону y= .
Определить суммарную стоимость перевозки
1 тонны груза на расстояние в 500 км.
.
Определить суммарную стоимость перевозки
1 тонны груза на расстояние в 500 км.
Вариант 7
 ;
9.
;
9.
 ;
;
 ;
10.
;
10. ;
;
 ;
11.
;
11. ;
;
 ;
12.
;
12. ;
;
 ;
13.
;
13. ;
;
 ;
14.
;
14.
 ;
;
 ;
15.
;
15.
 ;
;
 ;
16.
;
16.

17. Вычислить площадь фигуры, ограниченной линиями:
а) y=8+2x-x2, 2x-y+4=0 и y=0;
б)
y= (x>0), y=x, y=4x;
(x>0), y=x, y=4x;
в)
y= ,
y=0.
,
y=0.
18.
Зависимость, потребляемой на бытовые
нужды города электроэнергии y
(кВт.ч.), от времени суток х (в часах)
выражается следующей формулой y=а+b
cos
 (x+3).
Определить суммарный расход электроэнергии
за сутки. Провести расчет при а=25
т кВт.ч., b=15
т кВт.ч.
(x+3).
Определить суммарный расход электроэнергии
за сутки. Провести расчет при а=25
т кВт.ч., b=15
т кВт.ч.
Вариант 8
 ;
9.
;
9.
 ;
;
 ;
10.
;
10.
 ;
;
 ;
11.
;
11.
 ;
;
 ;
12.
;
12.
 ;
;
 ;
13.
;
13.
 ;
;
 ;
14.
;
14.
 ;
;
 ;
15.
;
15.
 ;
;
 ;
16.
;
16.
 .
.
Вычислить площадь фигуры, ограниченной линиями:
а) осью ОХ, y=(x+2)2 и y=4-x;
б) y=4-x2, y=0;
в)
y= ,
x=4
и осью ОХ.
,
x=4
и осью ОХ.
Две машины начали двигаться одновременно по прямой дороге в одном направлении. Одна двигалась со скоростью V1=3t2 м/сек, а другая – со скоростью V2=(6t2-10) м/сек. На каком расстоянии они будут друг от друга через 10 сек?
Вариант 9
 ;
9.
;
9.
 ;
;
 ;
10.
;
10.
 ;
;
 ;
11.
;
11.
 ;
;
 ;
12.
;
12.
 ;
;
 ;
13.
;
13.
 ;
;
 ;
14.
;
14.
 ;
;
 ;
15.
;
15.
 ;
;
 ;
16.
;
16.
 .
.
Вычислить площадь фигуры, ограниченной линиями:
а) y=3x-x2, x2=2y;
б) y=ex, y=e-x, x=2;
в) xy=4, x+y-5=0.
Функция y=2t+5t2 устанавливает интенсивность поступления продукции с конвейера предприятия на склад в любой момент времени, отсчитываемый в часах от начала поступления продукции на склад. Найти запас продукции, поступившей на склад за первые 2 часа приема, если считать продукцию непрерывно поступающей на склад.
Вариант 10
 ;
9.
;
9.
 ;
;
 ;
10.
;
10.
 ;
;
 ;
11.
;
11.
 ;
;
 ;
12.
;
12.
 ;
;
 ;
13.
;
13.
 ;
;
 ;
14.
;
14.
 ;
;
 ;
15.
;
15.
 ;
;
 ;
16.
;
16.
 .
.
Найти площадь фигуры, ограниченной линиями:
а) y=2x-x2 и y= -x;
б)
y=sin x, осью
ОХ, х=0,
х=2 ;
;
в) xy=3 и x+y=4.
Определить стоимость перевозки а тонн груза по железной дороге на расстояние b км, если тариф y на перевозки 1 тонны убывает за каждый следующий километр по сравнению с предыдущим на одну и ту же величину с рублей.
Вариант 11
 ;
9.
;
9.
 ;
;
 ;
10.
;
10.
 ;
;
 ;
11.
;
11.
 ;
;
 ;
12.
;
12.
 ;
;
 ;
13.
;
13.
 ;
;
 ;
14.
;
14.
 ;
;
 ;
15.
;
15.
 ;
;
 ;
16.
;
16.
 .
.
Вычислить площадь фигуры, ограниченной линиями:
а) y=ex, y=e-x, x=1;
б)
y=x2,
y= ;
;
в) y2=6x, x2+y2=16.
Зная, что среднее значение непрерывной на отрезке [а; b] функции находится по формуле
 .
Найти среднее значение издержек
К(х)=3х2+4х+2,
выраженных в денежных единицах, если
объем продукции х меняется от 0 до 3
единиц. Указать объем продукции, при
котором издержки принимают среднее
значение.
.
Найти среднее значение издержек
К(х)=3х2+4х+2,
выраженных в денежных единицах, если
объем продукции х меняется от 0 до 3
единиц. Указать объем продукции, при
котором издержки принимают среднее
значение.
Вариант 12
 ;
9.
;
9.
 ;
;
 ;
10.
;
10.
 ;
;
 ;
11.
;
11.
 ;
;
 ;
12.
;
12.
 ;
;
 ;
13.
;
13.
 ;
; ;
14.
;
14.
 ;
;
 ;
15.
;
15.
 ;
;
; 16.
 .
.
Вычислить площадь фигуры, ограниченной линиями:
а) xy=4, x+y-5=0 ;
б) y2+x=4, y2-3x=12;
в)
y= и ее асимптотой.
и ее асимптотой.
Найти дневную выработку Р за рабочий день продолжительностью 8 часов, если производительность труда в течение дня меняется по формуле р=f(t)=р0(-0,2t2+1,6t+3), где t – время (ч), р0 (единица продукции/ч) – производительность на начало смены.
Вариант 13
 ;
9.
;
9.
 ;
;
 ;
10.
;
10.
 ;
;
 ;
11.
;
11.
 ;
;
 ;
12.
;
12.
 ;
;
 ;
13.
;
13.
 ;
;
 ;
14.
;
14.
 ;
;
 ;
15.
;
15.
 ;
;
 ;
16.
;
16.
 .
.
Найти площадь фигуры, ограниченной линиями:
а) y=x3, y=8, x=0;
б) y2+8x=16, y2-24x=48;
в)
x2+y2=8,
y= .
.
Определить количество автомобилей, выпущенных за 5 лет, если годовой выпуск рос в арифметической прогрессии f(t)=a0+b0t.
Вариант 14
 ;
9.
;
9.
 ;
;
 ;
10.
;
10.
 ;
;
 ;
11.
;
11.
 ;
;
 ;
12.
;
12.
 ;
;
 ;
13.
;
13.
 ;
;
 ;
14.
;
14.
 ;
;
 ;
15.
;
15.
 ;
;
 ;
16.
;
16.
 .
.
Найти площадь фигуры, ограниченной линиями:
а) y2=4x, xy=2, x=4;
б) y= , y=x-2, x=0;
в) + y2=1.
Определить дисконтированный доход за четыре года при процентной ставке 6%, если первоначальные капиталовложения составили 8 млн руб. и намечается ежегодно увеличивать капиталовложения на 2 млн руб.
Вариант 15
 ;
9.
;
9.
 ;
;
 ;
10.
;
10.
 ;
;
 ;
11.
;
11.
 ;
;
 ;
12.
;
12.
 ;
;
 ;
13.
;
13.
 ;
;
 ;
14.
;
14.
 ;
;
 ;
15.
;
15.
 ;
;
 ;
16.
;
16.
 .
.
Найти площадь фигуры, ограниченной линиями:
а) y= , y=0, x=a, x=b (a>b>0);
б)
y= ,
y=2 -
,
y=2 - ;
;
в) y2=2x, x2+y2=3.
Найти полные издержки производства, если объем продукции равен 42 единицам, а зависимость издержек от объема имеет вид К(х)=х3-2х2+х.
Вариант 16
 ;
9.
;
9.
 ;
;
 ;
10.
;
10.
 ;
;
 ;
11.
;
11.
 ;
;
 ;
12.
;
12.
 ;
;
 ;
13.
;
13.
 ;
;
 ;
14.
;
14.
 ;
;
 ;
15.
;
15.
 ;
;
 ;
16.
;
16.
 .
.
Найти площадь фигуры, ограниченной линиями:
а) y=sin x, y=0, 0 x ;
б) y=e-x, x=0, y=0, x=a;
в) y=ln x, осью ОХ и прямой х=2.
Определить объем продукции, произведенной рабочим за пятый час рабочего дня, если производительность труда характеризуется функцией f(t)=
 +5.
+5.
Вариант 17
 ;
9.
;
9.
 ;
;
 ;
10.
;
10.
 ;
;
 ;
11.
;
11.
 ;
;
 ;
12.
;
12.
 ;
;
 ;
13.
;
13.
 ;
;
 ;
14.
;
14.
 ;
;
 ;
15.
;
15.
 ;
;
 ;
16.
;
16.
 .
.
Найти площадь фигуры, ограниченной линиями:
а) xy= -1, y= -x2, x=2;
б) y=2x-x2, y=x;
в) xy=3 и прямой, проходящей через точки (1, 4), (0,5; 6).
Найти объем продукции, произведенной за 5 лет, если функция Кобба-Дугласа имеет вид g(t)=(2+t)e4t.
Вариант 18
 ;
9.
;
9.
 ;
;
 ;
10.
;
10.
 ;
;
 ;
11.
;
11.
 ;
;
 ;
12.
;
12.
 ;
;
 ;
13.
;
13.
 ;
;
 ;
14.
;
14.
 ;
;
 ;
15.
;
15.
 ;
;
 ;
16.
;
16.
 .
.
Найти площадь фигуры, ограниченной линиями:
а) y=3x-x2, x2=2y;
б)
y=sin x, y=cos x, 0
x
 ;
;
в) y=4x-x2+1 и касательными к параболе, проведёнными в точках с абсциссами x1=0, x2=3.
Определить запас товаров на складе, образуемый за два дня, если поступление товаров характеризуется функцией f(t)= 3t2+3t+4.
Вариант 19
 ;
9.
;
9.
 ;
;
 ;
10.
;
10.
 ;
;
 ;
11.
;
11.
 ;
;
 ;
12.
;
12.
 ;
;
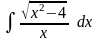 ;
13.
;
13.
 ;
;
 ;
14.
;
;
14.
;
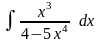 ;
15.
;
15.
 ;
;
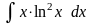 ;
16.
;
16.
 .
.
Найти площадь фигуры, ограниченной линиями:
а) y=x2-6x+8, x+y-2=0;
б)
y=x-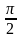 ,
y=cos x, x=0;
,
y=cos x, x=0;
в) y= -2(x-3)2+2 и y=0.
Определить объем продукции, произведенной рабочим за третий час рабочего дня, если производительность труда характеризуется функцией f(t) =
 .
.
Вариант 20
 ;
9.
;
9.
 ;
;
 ;
10.
;
10.
 ;
;
 ;
11.
;
11.
 ;
;
 ;
12.
;
12.
 ;
;
 ;
13.
;
13.
 ;
; ;
14.
;
14.
 ;
;
 ;
15.
;
15.
 ;
;
 ;
16.
;
16.
 ;
;
Найти площадь фигуры, ограниченной линиями:
а) y2=4x, x2=4y;
б) y= , y= ;
в) y=x2+4x+9 и касательными к параболе, проведёнными в точках с абсциссами x1=0, x2= -3.
Среднее значение непрерывной на отрезке [а; b] функции находится по формуле f()=
 .
Найти среднее значение издержек
k(x)=6x2+4x+1
(ден.ед.), если объем продукции х меняется
от 0 до 5 единиц. Указать объем продукции,
при котором издержки принимают среднее
значение.
.
Найти среднее значение издержек
k(x)=6x2+4x+1
(ден.ед.), если объем продукции х меняется
от 0 до 5 единиц. Указать объем продукции,
при котором издержки принимают среднее
значение.
