7. Метод наименьших квадратов
В экономической практике часто требуется представить наблюдаемые (измеренные) данные в виде функциональной зависимости. При этом предполагается, что вид функциональной зависимости известен (например, в результате ранее проведенного исследования) и требуется определить только параметры этой зависимости.
Пусть
в ходе исследования (например
покупательского спроса) получена
следующая таблица, где
- аргумент (цена товара), а у
- функция (кол-во товара).
|
|
|
… |
|
|
|
|
… |
|
Требуется по этим табличным данным получить функциональную зависимость (кривую спроса).
Эта
функциональная зависимость либо
линейная:
либо квадратичная
Метод
наименьших квадратов предусматривает
нахождение параметров
этих зависимостей из условия минимума
суммы квадратов отклонений
.
Для линейной зависимости:
Для квадратичной зависимости:
В первом случае
функция
от двух переменных, а
- от трёх переменных. Минимум – это
экстремум, а необходимое условие
экстремума
Из условий (необходимым) получаются формулы для определения коэффициентов линейной зависимости.
Из
условий
следует формула для квадратичной
линейной зависимости:
Пример. В результате исследования зависимости между сроком эксплуатации автомобиля и расходами на его ремонт получены следующие данные:
t, лет |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
S, тыс. руб |
12 |
14 |
23 |
37 |
44,5 |
57 |
65,5 |
77 |
Найти линейную зависимость стоимости ремонта автомобиля от срока эксплуатации; предлагаемую величину затрат на ремонт за 10-й год эксплуатации.
n |
t,
лет = |
|
|
|
1 |
1 |
12 |
1 |
12 |
2 |
2 |
14 |
4 |
28 |
3 |
3 |
23 |
9 |
69 |
4 |
4 |
37 |
16 |
148 |
5 |
5 |
44,5 |
25 |
222,5 |
6 |
6 |
57 |
36 |
342 |
7 |
7 |
65,5 |
49 |
458,5 |
8 |
8 |
77 |
64 |
616 |
|
36 |
330 |
204 |
1896 |
Получаем
систему линейных уравнений:
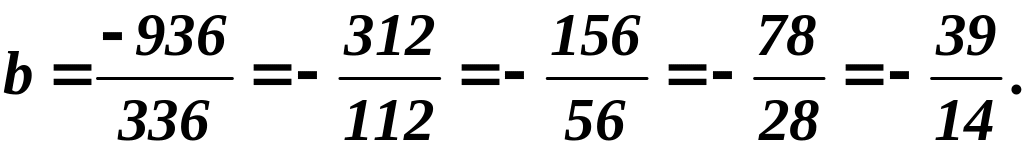
Функция зависимости стоимости ремонта автомобиля от срока эксплуатации имеет вид:
При
