
- •Лекция 9. Прямая линия на плоскости. Кривые второго порядка.
- •9.1 Прямая линия на плоскости.
- •9 .2. Векторное уравнение прямой.
- •9.3. Общее уравнение прямой и его исследование
- •Правило составления уравнения прямой
- •Правило составления уравнения прямой l , для которой известны координаты точки м1 (х1;у1) и задано какое-либо второе условие, состоит в следующем:
- •9.4. Уравнение прямой с угловым коэффициентом
- •9.5. Уравнение прямой в отрезках
- •Свойство перпендикулярности двух векторов
- •9.10. Кривые второго порядка
- •9.10.1 Окружность
- •9.10.2. Эллипс
- •9.10.3 Гипербола
- •9.10.4 Парабола
- •Прямая на плоскости и кривые второго порядка
- •1. Даны вершины треугольника .
- •Для эллипса и гиперболы:
- •Для параболы:
9.10. Кривые второго порядка
9.10.1 Окружность
Определение 9.7. Окружностью называется геометрическое место точек, равноудаленных от одной данной точки, называемой центром.
Вывод
уравнения:
Пусть в декартовой системе координат
дана окружность с центром в точке
![]() .
.
 Пусть
- произвольная точка окружности. Радиус
СМ
можно найти как расстояние между точкой
С
и точкой М.
Пусть
- произвольная точка окружности. Радиус
СМ
можно найти как расстояние между точкой
С
и точкой М.
 .
.
Возводя
в квадрат:
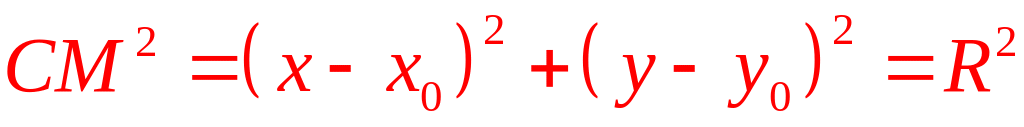 (9.1)
(9.1)
Где
обозначили R
– радиус
окружности,
- координаты центра,
![]() - координаты точки, принадлежащей
окружности. В частности, если центр
окружности совпадает с началом координат.
То уравнение окружности (9.1) примет вид:
- координаты точки, принадлежащей
окружности. В частности, если центр
окружности совпадает с началом координат.
То уравнение окружности (9.1) примет вид:
![]() .
Раскроем в левой части (9.1) скобки, получим
.
Раскроем в левой части (9.1) скобки, получим
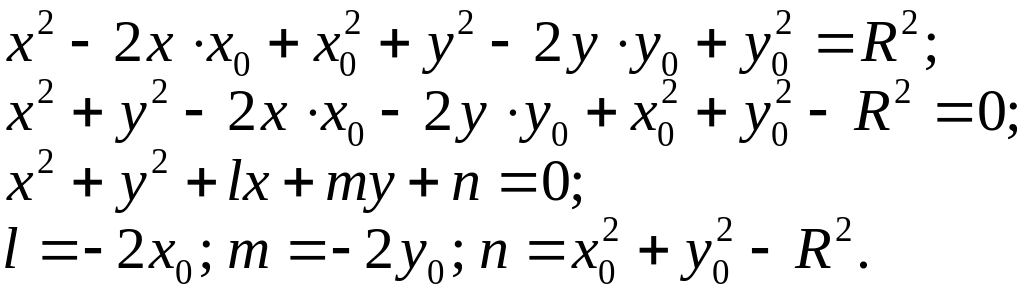 (9.2)
(9.2)
Составим
число
![]() .
В общем случае уравнение (9.2) определяет
окружность, если:
.
В общем случае уравнение (9.2) определяет
окружность, если:
![]() - окружность,
- окружность,
![]() - уравнение
окружности нулевого радиуса,
- уравнение
окружности нулевого радиуса,
![]() - мнимая окружность.
- мнимая окружность.
Взаимное
расположение точки
![]() и окружности
определяется условиями:
и окружности
определяется условиями:
если
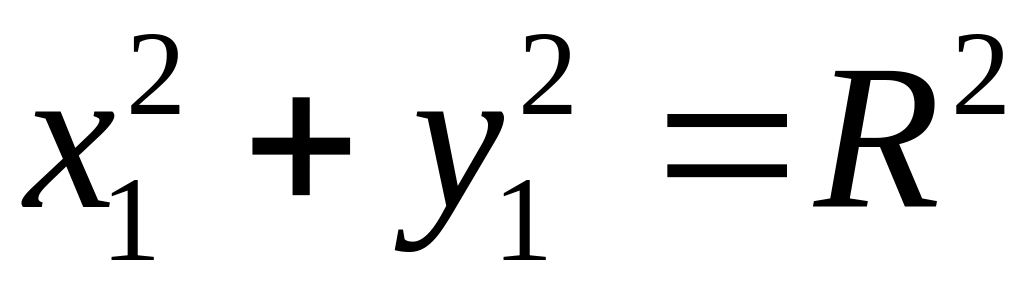 - точка М
принадлежит
окружности,
- точка М
принадлежит
окружности,если
 - точка М
лежит вне окружности,
- точка М
лежит вне окружности,если
 - точка М
лежит внутри окружности.
- точка М
лежит внутри окружности.
9.10.2. Эллипс
Определение 9.8. Эллипсом называется геометрическое место точек на плоскости, сумма расстояний от каждой из которых до двух заданных точек,

называемых фокусами, есть величина постоянная (ее обозначают 2а), большая, чем расстояние между фокусами.
Обозначаются
фокусы
![]() ,
т.е. расстояние между ними обозначается
2с,
причем сумма расстояний от любой точки
эллипса до фокусов:
,
т.е. расстояние между ними обозначается
2с,
причем сумма расстояний от любой точки
эллипса до фокусов:
![]() .
Пусть точка М
– произвольная точка эллипса.
.
Пусть точка М
– произвольная точка эллипса.
Определение
9.9. Величины
![]() называются фокальными радиусами точки
М.
называются фокальными радиусами точки
М.
По
определению эллипса:![]() .
.
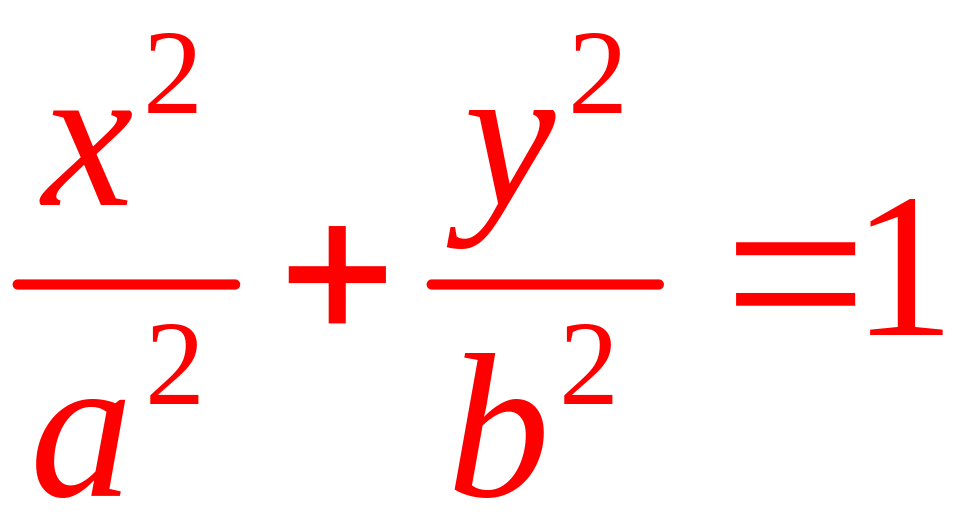 - каноническое
уравнение эллипса.
- каноническое
уравнение эллипса.
Здесь
а
– большая (откладывается по оси Ох),
b
– малая полуоси эллипса (по Оу).
Причём
![]() - половина расстояния между фокусами
связаны соотношением
- половина расстояния между фокусами
связаны соотношением
![]() .
.
Форма эллипса (мера его сжатия) характеризуется его эксцентриситетом.
Определение 9.10. Эксцентриситетом эллипса называется отношение расстояния между фокусами к длине большей полуоси.
Обозначается:
 .
Так как
.
Так как
![]() ,
то
,
то
![]() .
.
Если величина эксцентриситета приближается к единице, то эллипс сильно вытянут; если же величина эксцентриситета приближается к нулю, то эллипс имеет более округлую форму. Если величина эксцентриситета равна нулю, то эллипс вырождается в окружность.
Фокальные радиусы выражаются через абсциссу точки эллипса по формулам:
![]() -
(правый фокальный радиус),
-
(правый фокальный радиус),
![]() -
(левый фокальный радиус).
-
(левый фокальный радиус).
Взаимное
расположение точки
и эллипса
 :
:
если
 ,
точка М
принадлежит
эллипсу,
,
точка М
принадлежит
эллипсу,если
 ,
точка М
вне эллипса,
,
точка М
вне эллипса,если
 ,
точка М
внутри эллипса.
,
точка М
внутри эллипса.
9.10.3 Гипербола
Определение
9.10. Гиперболой
называется геометрическое место точек
плоскости, абсолютная величина разности
расстояний которых до двух данных точек,
называемых фокусами, есть величина
постоянная (ее обозначают 2а).
Причем эта постоянная меньше расстояния
между фокусами (2с).Т .е.
.е.
![]() ;
;
![]()
Выберем
декартову систему координат, приняв за
ось х
прямую, проходящую через фокусы
![]() и
.
и
.
![]() .
.
Расстояние
от точки М
до фокусов
:

Так
как
,
то

Возводя в квадрат и группируя слагаемые, получим:
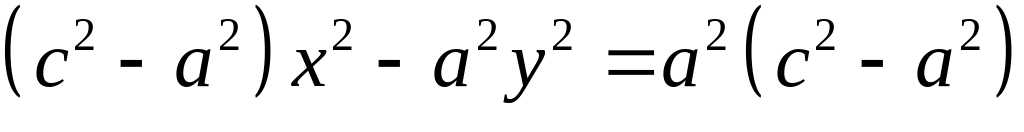
Из
![]() :
:
![]() ,
,
![]()
![]() Обозначается:
Обозначается:
![]() .
.
![]() ;
;
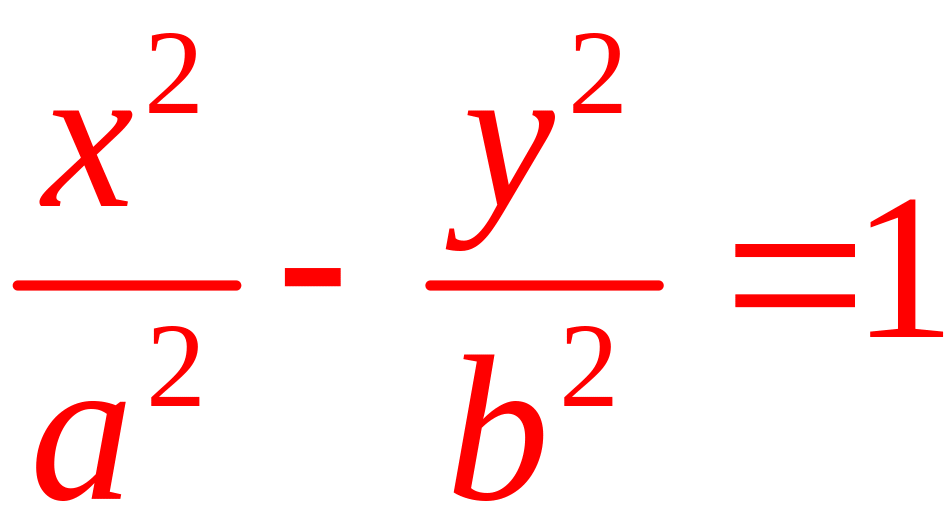 - каноническое
уравнение гиперболы, где
- каноническое
уравнение гиперболы, где
![]() .
.
Гипербола
состоит из 2-х ветвей и расположена
симметрично относительно осей координат.
Точки
![]() называются вершинами
гиперболы.
Отрезок
называются вершинами
гиперболы.
Отрезок
![]() такой, что
такой, что
![]() называется действительной
осью
гиперболы, а отрезок
называется действительной
осью
гиперболы, а отрезок
![]() такой, что
такой, что
![]() - мнимой
осью.
- мнимой
осью.
 Определение
9.11. Прямая
называется асимптотой
гиперболы, если расстояние точки
гиперболы от этой прямой стремится к
нулю при
Определение
9.11. Прямая
называется асимптотой
гиперболы, если расстояние точки
гиперболы от этой прямой стремится к
нулю при
![]() .
.
Гипербола
имеет две асимптоты, уравнения которых
:
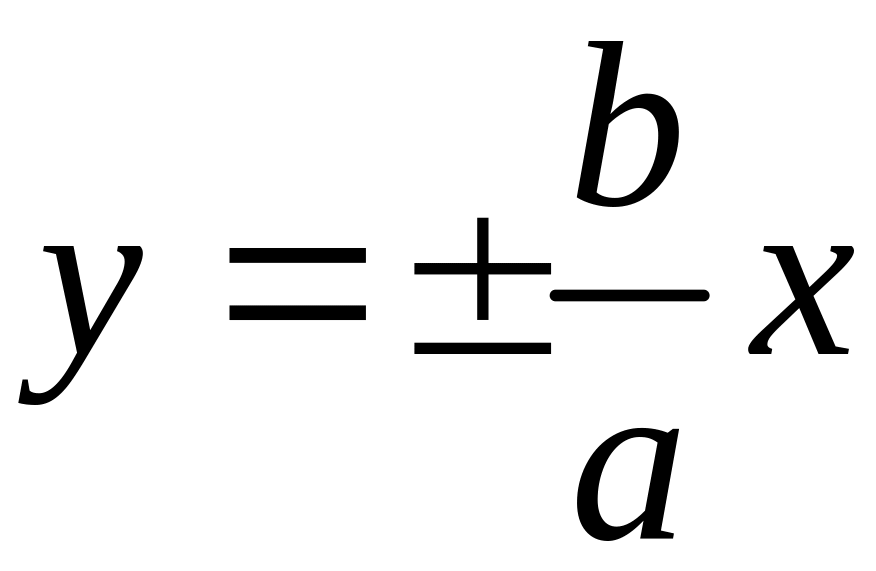 .
.
Определение
9.12. Отношение
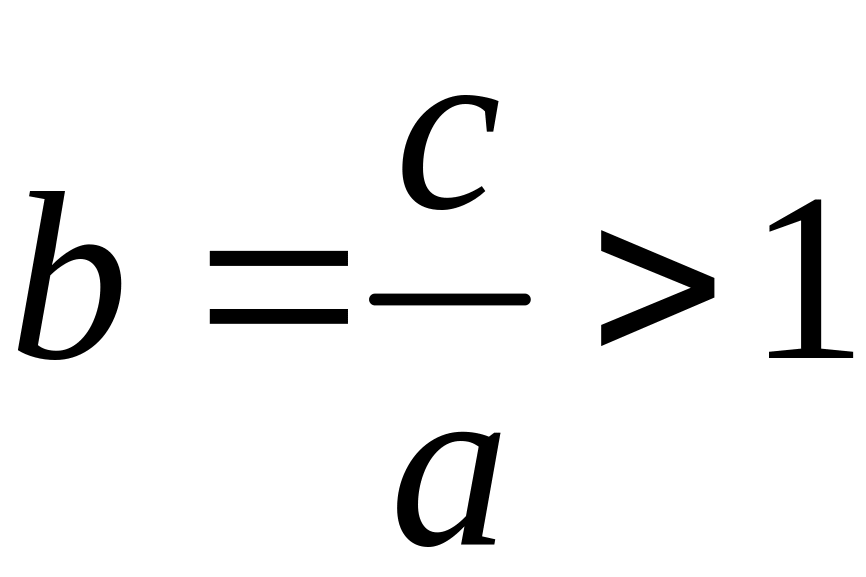 ,
называется эксцентриситетом
гиперболы.
,
называется эксцентриситетом
гиперболы.
Фокальные радиусы правой ветви гиперболы:
![]() (правый фокус-радиус),
(правый фокус-радиус),
![]() (левый фокус-радиус).
(левый фокус-радиус).
Фокальные радиусы левой ветви гиперболы:
![]() (правый),
(правый),
![]() (левый).
(левый).
В
частности, если
![]() ,
то уравнение гиперболы принимает вид:
,
то уравнение гиперболы принимает вид:
![]() и называется
равнобочной.
Её асимптоты образуют прямой угол.
и называется
равнобочной.
Её асимптоты образуют прямой угол.
Если
за оси координат принять асимптоты, то
уравнение гиперболы будет иметь вид
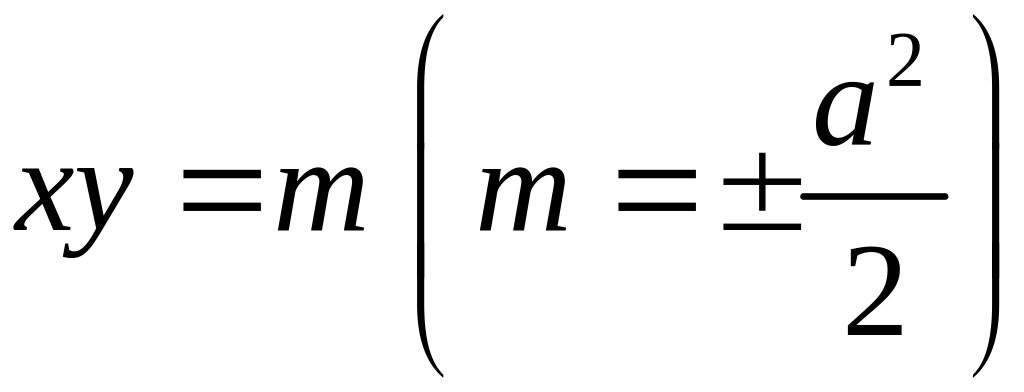 ;
;
при
![]() ,
гипербола расположена в I и III координатных
углах,
,
гипербола расположена в I и III координатных
углах,
при
![]() ,
гипербола расположена во II и IV
координатных углах.
,
гипербола расположена во II и IV
координатных углах.
Уравнения
 или
или
 также являются уравнениями гиперболы,
но действительной осью этой гиперболы
служит отрезок оси
длины 2b.
также являются уравнениями гиперболы,
но действительной осью этой гиперболы
служит отрезок оси
длины 2b.
