Свойство перпендикулярности двух векторов

Два вектора перпендикулярны тогда и только тогда, когда их скалярное произведение .

Распишем скалярное произведение векторов в координатах и получим условие перпендикулярности двух прямых : .

Пусть теперь прямые заданы уравнениями с угловыми коэффициентами .

Прямые параллельны тогда и только тогда, когда равны их угловые коэффициенты, т.е. .

Две прямые перпендикулярны тогда и только тогда, когда произведение их угловых коэффициентов равно –1; т.е. .

Расстояние от точки до прямой – длина перпендикуляра - находится по формуле: , где - координаты точки , - уравнение прямой.

Обобщённая таблица по теме: «Уравнение линии на плоскости»

№/п	Условия	Уравнение прямой
1	Векторное уравнение прямой
2	Векторное уравнение прямой в координатной форме
3	Каноническое уравнение прямой
4	Общее уравнение прямой
5	Уравнение прямой, проходящей через точку перпендикулярно вектору
6	Уравнение прямой, проходящей через точку параллельно вектору
7	Уравнение прямой с угловым коэффициентом
8	Уравнение прямой в отрезках, где а и в – соответственно абсцисса и ордината точек пересечения прямой с осями ОХ и ОУ
9	Уравнение пучка прямых, проходящих через данную точку
10	Уравнение прямой, проходящей через две заданные точки и
11	Уравнение прямой, проходящей через данную точку в заданном направлении
12	Угол между двумя прямыми, заданными нормальными векторами прямых
13	Угол между двумя прямыми, заданными уравнениями с угловыми коэффициентами ;
14	Угол между двумя прямыми, заданными общими уравнениями и
15	Угол между двумя прямыми, заданными каноническими уравнениями и
16	Условие параллельности двух прямых, заданными уравнениями с угловыми коэффициентами ;
17	Условие параллельности двух прямых, заданными общими уравнениями
18	Условие параллельности двух прямых, заданными каноническими уравнениями и
19	Условие перпендикулярности двух прямых, заданными уравнениями с угловыми коэффициентами ;
20	Условие перпендикулярности двух прямых, заданными общими уравнениями и
21	Условие перпендикулярности двух прямых, заданными каноническими уравнениями и
22	Расстояние от точки до прямой
23	Координаты точки , делящей отрезок с концами и в отношении , т.е.
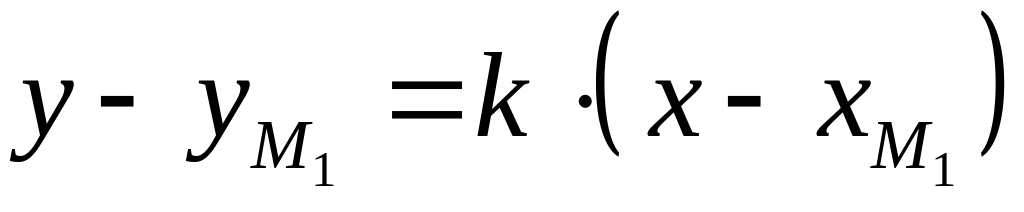
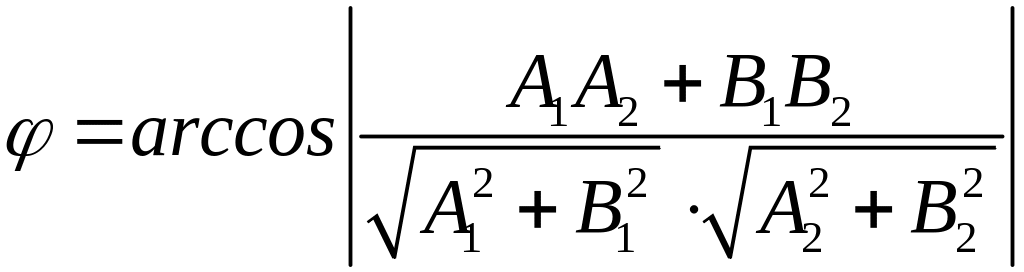
24	Координаты точки - середины отрезка с концами в точках и