Правило составления уравнения прямой

Положение прямой на плоскости относительно системы координат можно задать различными способами:

1. точкой и направлением;

2. точкой и перпендикулярным прямой вектором;

3. двумя точками;

4. отрезками, которые прямая отсекает на осях координат.

Во всех случаях задания прямой обязательно должна быть известна хотя бы одна точка, через которую проходит искомая прямая и дополнительное условие: коллинеарности, перпендикулярности или вторая точка, принадлежащая прямой.

Правило составления уравнения прямой l , для которой известны координаты точки м1 (х1;у1) и задано какое-либо второе условие, состоит в следующем:

1) На прямой l выбирают произвольную точку с текущими координатами х,у :

М ( х; у) .

2) Находят координаты вектора, лежащего на прямой l и такого, что его начало есть точка М₁ (х₁;у₁), а конец точка М ( х; у), то есть вектор М₁М=( х-х₁;у-у₁).

3) Записывают координаты вектора, заданного дополнительными условиями (коллинеарности, перпендикулярности, двумя точками), то есть направляющего или нормального вектора .

4). Используют условие коллинеарности или перпендикулярности векторов и М₁М.

9.4. Уравнение прямой с угловым коэффициентом

Пусть дана ось Ох и прямая l.

О пределение 9.3. Углом между осью и прямой называют угол, на который нужно повернуть ось, чтобы она совпала с заданной прямой или стала ей параллельна.

Определение 9.4. Угловым коэффициентом прямой называется тангенс угла наклона этой прямой к положительному направлению оси Ох. Обозначается так: . Выразим из общего уравнения (9.4) при условии, что переменную у: . Полагая, что получим:

-уравнение прямой с угловым коэффициентом, (9.5)

где , а b – ордината точки пересечения прямой с осью Oy.

9.5. Уравнение прямой в отрезках

Пусть прямая не параллельна ни одной из осей координат и не проходит через точку О. Тогда она задается уравнением (9.4): , где . Она (прямая) будет пересекать оси координат в точках . Т.к. точки , то их координаты удовлетворяют уравнению (9.4). Подставим координаты точки P и Q:

Для P: ;

Для Q: ; .

Подставляя полученные A и В в (9.4): 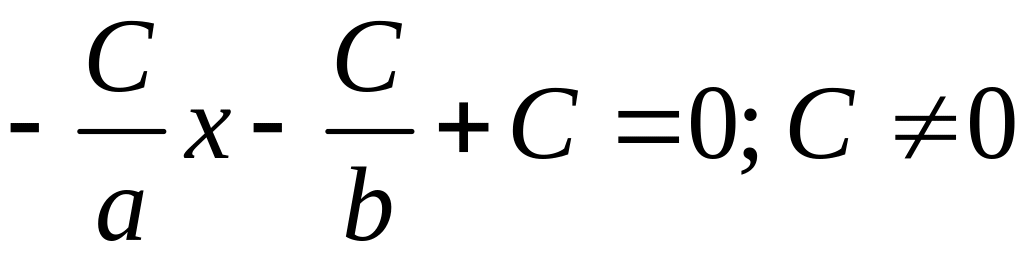. Разделим всё уравнение на . Получим: - уравнение прямой в отрезках, (9.6), где а – абсцисса точки пересечения с осью Ох, b – ордината точки пересечения с осью Оу.

9.6. Уравнение пучка прямых, проходящих через данную точку

Пусть на прямой l задана точка .Запишем уравнение с угловым коэффициентом: (9.5). Т.к. , то её координаты удовлетворяют уравнению: . Вычтем из (9.5) соответствующие части последнего уравнения получим: - уравнение пучка прямых, (9.7), проходящих через данную точку .

9.7. Уравнение прямой, проходящее через две заданные точки

Пусть на прямой даны две точки . Запишем уравнение (9.7) для точки А: , (9.8)

Т.к. точка , то координаты точки В удовлетворяют уравнению (9.8):

(9.9)

Считая, что . Поделим (9.8) на (9.9): - уравнение прямой, проходящей через две точки (9.10).

9.8. Угол между двумя прямыми

Определение 9.5. Углом между двумя прямыми будем называть угол, на который нужно повернуть прямую , чтобы она совпала с или стала ей параллельна.

П усть прямые заданы: ;

; .

Из рисунка видно, что

Т.о., .

9.9. Условия параллельности и перпендикулярности дух прямых

Определение 9.6. Два вектора, лежащие на одной прямой или на параллельных прямых называются коллинеарными. Три вектора, лежащие в одной плоскости и параллельные одной плоскости называются компланарными.

Пусть даны две прямые и . Обе они имеют нормали с координатами: .

Теорема 9.1: Две прямые параллельны тогда и только тогда, когда коллинеарны их нормальные векторы.

Свойство коллинеарности двух векторов.

Для того, чтобы два вектора были коллинеарны, необходимо и достаточно, чтобы и координаты были пропорциональны, т.е.: 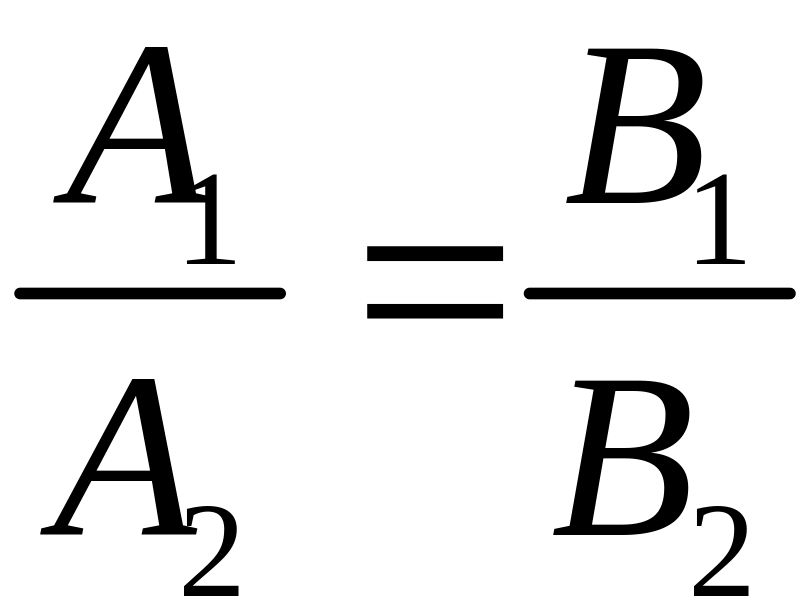- условие параллельности двух прямых.

Е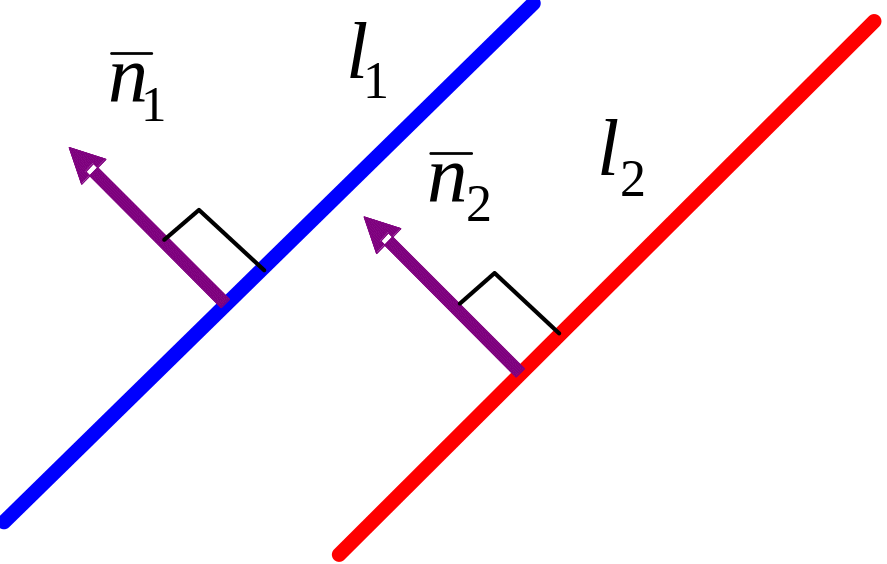 сли выполняется условие: , то прямые совпадают, т.к. одно уравнение получается из другого путём умножения на любое число.

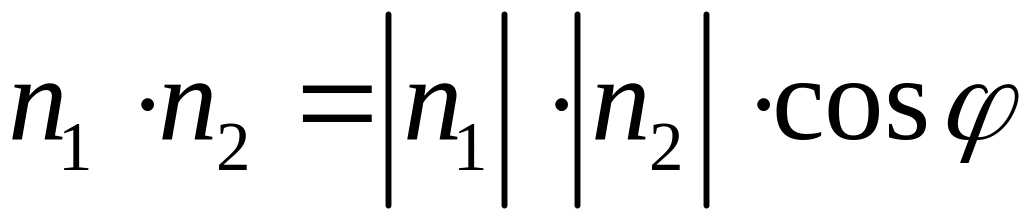Теорема 9.2 .(условие перпендикулярности двух прямых). Две прямые перпендикулярны тогда и только тогда, когда перпендикулярны их нормальные векторы, т.е. . Напомним определение: скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними, т.е. , т.к. , то .