Статистические методы в геологии лекции

vk.com/club152685050 | vk.com/id446425943

числом параметров. Например, при интерполяции алгебраическими полиномами необходимо рассматривать полиномы высоких степеней.

Но, как известно, из теории интерполяции, такие полиномы дают большие вычислительные погрешности. С другой стороны, при интерполяции «в целом» по всей области, при построении интерполирующего полинома используются значения ZI, расположенные друг от друга на значительном расстоянии, из чего может следовать их статистическая независимость.

Исходя из этого и во многих современных пакетах пространственного моделирования, используют методы локальной интерполяции (ЛИ).

Вметодах ЛИ при вычислении каждого интерполирующего значения используется не вся выборка, а только замеры, расположенные в некоторой окрестности, радиус которой обозначим R.

Вметодах ЛИ точность интерполяции сильно зависит от значения R. Ясно, что величина R должна определяться радиусом корреляции случайного параметра Z. Но на практике радиус корреляции не известен.

Различны методы интерполяции, реализованные в различных программных модулях, имеют параметры, задание которых позволяет осуществлять ЛИ. Например, метод радиальных базисных функций и метод Kriging.

Наиболее обоснованно значение R можно задавать в методе Kriging, в котором предусмотрено построение вариограмм по областям различной геометрии и размера.

Следует иметь в виду, что любая геологическая модель, как, впрочем, и всякая

модель, является приближенным описанием изучаемого объекта. Одним из видов погрешностей, осложняющих модель, являются ошибки алгоритма. Поэтому процесс построения модели не может заканчиваться построением карты, а должен быть продолжен анализом модели, в частности, выявлением и устранением алгоритмических ошибок.

Основные задачи анализа пространственных данных

Существует огромное количество пространственно распределенной информации, собранной в базы и банки данных по окружающей среде. Задача ее интерпретации, анализа и дальнейшего использования представляется чрезвычайно важной и требует комплексного системного подхода. Статистическоемоделирование пространственных явлений позволяет обобщить имеющиеся измерения и получить модель их распределения в пространстве.

Пространственное моделирование применяется во многих сферах человеческой деятельности. Так, при климатическом моделировании анализируются измерения

vk.com/club152685050 | vk.com/id446425943

температуры, осадков, скорости ветра и т. д. в различных точках пространства. При моделировании загрязнения окружающей среды используются измерения (пробы грунта, воды, воздуха, дистанционное зондирование) в различных местах. В задачах геологии моделируются свойства пород в промежутке между скважинами, где делаются измерения.

Глубокий анализ и моделирование пространственных данных требуют применения комплексного подхода и различных методов, характеризующих ту или иную особенность явления. Сложность такого анализа обусловлена несколькими факторами: наличием больших объемов количественной и качественной информации по исследуемому явлению, многомасштабностью и многопеременностью, наличием различных факторов влияния.

Постановка задачи

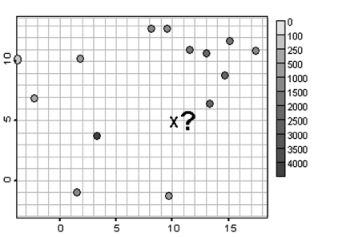
При работе с пространственными данными обычно имеется некоторое количество измерений изучаемой переменной в различных точках, число которых ограниченно. Итак, есть область, на которой проведен ряд измерений некоторой величины Z. Эти измерения проведены в произвольно распределенном по области наборе точек (x, y), которые мы будем называть сетью мониторинга (рис. 1.1). Но есть и участки области, не покрытые измерениями, о значениях величины Z в которых хотелось бы получить информацию. Наиболее часто требуется оценить значение наблюдаемой величины в непромеренной точке X на основе имеющихся данных, т. е. решить задачу интерполяции.

Данные измерений, как правило, дискретны и пространственно неоднородно распределены. Анализ данных и его результаты зависят от качества и количества исходных данных, от методов и моделей обработки данных.

Рис. 1.1. Постановка задачи пространственного оценивания Приведем здесь ряд конкретных задач, для решения которых необходимо

применение комплекса исследований с помощью методов геостатистики —статистики пространственно распределенной (региональной) информации:

-оценить значение в точке, где измерение не проводилось;

-нарисовать карту, построить изолинии (определить значения на плотной сетке);

-оценить ошибку интерполяционной оценки;

-оценить значение переменной, по которой мало измерений, используя значения другой коррелированной с ней переменной, по которой проведено много измерений;

vk.com/club152685050 | vk.com/id446425943

-определить вероятность того, что значения наблюдаемой переменной превысят заданный уровень в интересующей нас области;

-получить набор равновероятных стохастических пространственных реализаций распределения наблюдаемой переменной.

Первые три задачи — примеры задач регрессии или классификации (в зависимости от типа исходных значений). Две последние задачи относятся к вероятностному анализу и связаны с оценками риска.

Подходы к анализу пространственно-распределенных данных

Существует несколько подходов к анализу и обработке пространственно распределенных данных, которые можно условно разделить на три группы:

-детерминистические модели (интерполяторы) — линейная интерполяция на основе триангуляции, метод обратных расстояний в степени,мульти-квадратичные

уравнения и т. п.

-геостатистика — модели, базирующиеся на статистической интерпретации

данных;

-алгоритмы, основанные на обучении — искусственные нейронные сети, генетические алгоритмы, статистическая теория обучения машин векторов поддержки.

Конечно, это деление до известной степени условно. Так, геостатистические модели можно изложить в детерминистической формулировке, и наоборот, некоторые детерминистические модели имеют близкие статистические аналоги. В свою очередь, статистический подход, на котором базируется геостатистика, включает регрессионные модели пространственных интерполяций (предсказаний) и методы стохастического моделирования, цели и задачи которых различны. Алгоритмы, основанные на обучении (или искусственный интеллект), также имеют статистическую интерпретацию.

Современная геостатистика — это широкий спектр статистических моделей и инструментов для анализа, обработки и представления пространственно распределенной информации.

Традиционные детерминистические методы, широко используемые для пространственной интерполяции, позволяют решать только первую и вторую

задачи из приведенного выше списка. Геостатистическая теория позволяет решать весь набор задач, в том числе оценить неопределенность оценки и описать ее вариабельность.

Современная геостатистика — это быстро развивающаяся область приклад- ной статистики с огромным набором методов, линейных и нелинейных, пара- метрических и непараметрических моделей для анализа, обработки и пред-

ставления пространственной информации. Спектр ее применения весьма широк — от традиционного использования в области добычи ископаемых до современных приложений в экономике, финансах, окружающей среде, эпидемиологии.

Геостатистический анализ позволяет значительно повысить уровень на-

дежности и качество решений, принимаемых на основе использования пространственно распределенной информации. Современные тенденции геостатистики связаны с развитием методов стохастического моделирова-

vk.com/club152685050 | vk.com/id446425943

ния (пространственных аналогов методов Монте-Карло), методов, основан-

ных на многоточечной статистике, гибридных моделей с использованием алгоритмов искусственного интеллекта, с использованием дополнитель-

ной информации различного вида и приложениями в области обработки и передачи изображений, с расширением на временной и пространственно- временной анализы и многими направлениями.

Одним из важных составляющих традиционной геостатистики является пространственный корреляционный анализ, или вариография. Несмотря на кажущуюся простоту исходных формул, вариография позволяет сделать глубокие выводы о статистической природе данных и структуре адекват-

ных моделей. В принципе экспериментальная вариография, основанная на исходных данных, может быть использована в большинстве задач про-

странственного оценивания независимо от метода интерполяции наравне с традиционным статистическим анализом.

Основные этапы анализа и моделирования пространственных данных Кла́стер (англ. cluster — скопление, кисть, рой) — объединение нескольких

однородных элементов, которое может рассматриваться как самостоятельная единица, обладающая определёнными свойствами.

Если данные собраны на нерегулярной кластерной сети мониторинга, может потребоваться пространственная декластеризация для получения репрезентативной глобальной статистики — средних, вариаций, гистограмм. Если сеть мониторинга имеет зоны с заметно более высокой плотностью измерений, чем остальная область, то сеть мониторинга кластерная. Если при этом зоны повышенной плотности измерений характеризуются более высокими (или, наоборот, низкими) значениями измерений, возникает необходимость в декластеризации. Иначе оценки всех статистических характеристик будут искажены, например оценка среднего будет завышена (или, наоборот, занижена). Процедура декластеризации ориентирована на устранение такого рода искажений. Можно рассматривать два основных типа декластеризации — выборочную и весовую. Выборочная декластеризация связана с выбором части данных из кластеров, весовая предполагает задание весов, с которыми используются измерения.

Оценить некоторые пространственные особенности данных позволяет статистика с движущимся окном: область разбивается на подобласти, в каждой из которых проводится независимый статистический анализ.

Дальнейший пространственный анализ предполагает исследование и моделирование пространственной корреляции между данными по одной или нескольким переменным. Мерой пространственной корреляции является вариограмма — статистический момент второго порядка.

Для получения наилучшей в статистическом смысле пространственной оценки используются модели из семейства кригинга (kriging) — наилучшего линейного несмещенного оценивателя. Кригинг является «наилучшим» оценивателем в

статистическом смысле в классе линейных интерполяторов — его оценка обладает минимальной вариацией ошибки. Важное свойство кригинга — точное воспроизведение

vk.com/club152685050 | vk.com/id446425943

значений измерений в имеющихся точках (точный оцениватель). В отличие от многочисленных детерминистических методов, оценка кригинга сопровождается оценкой ошибки интерполяции в каждой точке. Полученная ошибка позволяет охарактеризовать неопределенность полученной оценки данных при помощи доверительных интервалов или «толстых» изолиний.

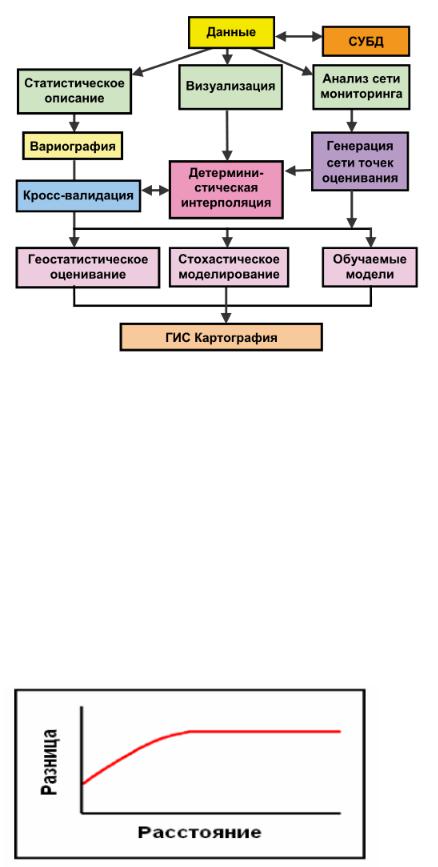
На основе описанных этапов анализа и моделирования пространственных данных можно сформулировать блок-схему пошагового анализа (рис. 1.2).

Рис. 1.2. Блок-схема методологии последовательного анализа и моделирования пространственно-распределенных данных

Вариограммы

Важным аспектом осуществления любых геостатистических расчетов является понимание того, как значения данных меняются с расстоянием и изменением направления. Вариограмма – это графический инструмент, который может быть использован для этого.

1. Введение в вариограммы

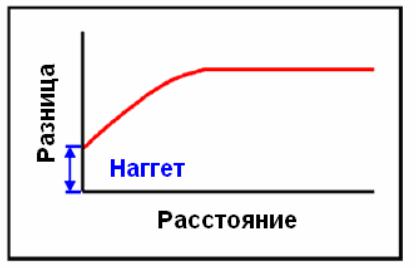
Вариограмма – это график, который сравнивает разницу значений в образцах на разных расстояниях друг от друга:

vk.com/club152685050 | vk.com/id446425943

Пример вариограммы

«Наггет» – самородковый эффект Если вы разделите единичный образец и пошлете его в две различные лаборатории,

то часто в результате вы получите различные содержания. Таким образом, при разделяющем образцы расстоянии, равном 0, присутствует разница в содержаниях.

Эта разница, именуемая НАГГЕТ (англ. – самородок) или САМОРОДКОВЫЙ ЭФФЕКТ, часто для красткости обозначается «с(0)». Величина самородка характеризуется, как разница в содержаниях при величине разделяющей дистанции 0.

Наггет – Самородковый Эффект Термин «Наггет» пришел в геостатистику при оценке месторождений золота, в

котором встречаются его самородные скопления. При разделении образца одна половина может содержать самородок золота, а другая не содержать золота вовсе. Хотя разница между частями, на которые разделен образец, часто объясняет это явление, человеческий фактор также может этому способствовать. Ошибки могут происходить при опробовании, в лаборатории, при вводе данных. Любая из них или все сразу могут способствовать формированию «Наггета». Эти аспекты часто обуславливают формирование «наггета». Они не рассматриваются в данном руководстве, но вы должны о них помнить так же, как и об их воздействии на последующие геостатистические вычисления.

«Силл»

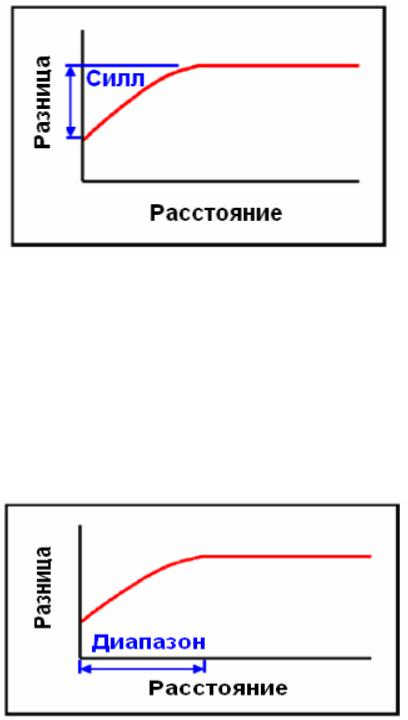
Если мы сравнивам два образца, расположенных на некотором расстоянии друг от друга, мы можем ожидать, что разница между ними будет больше, чем разница между теми образцами, которые расположены ближе друг к другу. Часть графика вариограммы, которая поднимается вправо и вверх от точки Наггета, отражает такую ситуацию.

В некоторой точке разница между образцами уже не может быть больше достигнутой. Например, максимальное значение в пробах минус минимальное значение в пробахдает нам наибольшую разницу между образцами. На вариограмме максимальная разница показана горизонтальным фрагментом графика.

vk.com/club152685050 | vk.com/id446425943

Две величины описывают точку, в которой вариограмма достигает своего максимального значения - силл (порог) и диапазон.

Силл

Силл (иногда коротко обозначаемый буквой “C”), как показано выше, является

разностью между максимальной разницей и наггетом. Термин «отношение Наггета к Силлу» используется для того, чтобы охарактеризовать процентную долю «суммарного Силла», которую занимает Наггет, и вычисляется следующим образом:

Отношение Наггета к Силлу = Наггет/ (Наггет +Силл)

Диапазон

Расстояние, на котором график достигает Силла, называется диапазон:

Диапазон

Диапазон (иногда коротко обозначаемый буквой “A”) представляет собой

максимальноерасстояние, на котором пары образцов еще могут быть соотнесены с разделяющей ихдистанцией (или на котором полностью исчезает корреляция между парами образцов).

За пределами диапазона корреляция полностью отсутствует.

vk.com/club152685050 | vk.com/id446425943

2. Расчет вариограммы

Чтобы рассчитать вариограмму, набор данных группируется в пары, которые разделены определенным расстоянием, именуемым «шагом». Затем следующие вычисления производятся для всех образцов в каждом интервале:

гамма (h) =сумма (разность между значениями в парах)2/2 x число пар

Чтобы продемонстрировать процесс, мы используем расположенные ниже данные. Предположим, что значения представляют пробы, отобранные по интервалам в 1

метр вдоль линии юг – север:

Чтобы создать график вариограммы «Расстояние против Разности», мы должны сначала выбрать величину шага (или интервал шага). Затем мы сгруппируем данные в пары образцов, которые попадают в каждый интервал шага. Для первого интервала, равного 1, мы получим следующие пары: 3-3, 3-4, 4-6 и т.д.… Разница между двумя

значениями возводится в квадрат и вычисляется сумма всех возведенных в квадрат разностей:

Затем сгруппируем пары все образцов, разделенных расстоянием 2, и вновь произведем расчет:

vk.com/club152685050 | vk.com/id446425943

vk.com/club152685050 | vk.com/id446425943