3.1.2.3. Синтез в базисе не и

Напомним, что элемент НЕ И реализует функцию, представляющую функционально полную систему, следовательно, любая комбинационная схема может быть построена только из элементов НЕ И.

Рассмотрим отдельную ДНФ, предположив, что в нашем распоряжении имеются элементы НЕ И с любым числом входов. Пусть в предлагаемом примере ДНФ имеет вид

. (1)

Расставим инверсии и скобки следующим образом:

. (2)

Опустив скобки на переменные по правилам Де Моргана, получим выражение, совпадающее с (1). Из эквивалентности выражений (1), (2) следует, что, построив схему в базисе ДНФ, используя выражение (1), можно затем заменить все элементы на НЕ И согласно выражению (2). В результате имеем схему:

Правила Де Моргана:

( )= &

( )= 

=

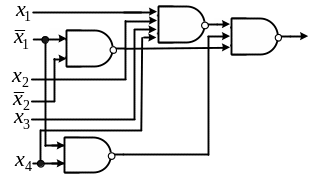
Рис. 3.7

КАДР

3.1.2.4. Синтез в базисе не или

Элемент НЕ ИЛИ также реализует функцию, представляющую функционально полную систему, следовательно, любая комбинационная схема может быть построена из элементов НЕ ИЛИ. Рассмотрим произвольную ДНФ, предположив, что в нашем распоряжении имеются элементы НЕ ИЛИ с произвольным числом входов. Пусть в предлагаемом примере ДНФ имеет вид

. (3)

Перейдем к выражению (4):

. (4)

Опустим инверсии со скобок на переменные. Получим выражение (5)

. (5)

Сравнив выражения (3) и (5), видим, что они представляют двойственные функции. Следовательно, при построении схемы в базисе ДНФ с последующей заменой всех элементов на НЕ ИЛИ реализуется функция, двойственная исходной функции.

Для построения заданной функции необходимо найти представление двойственной ей функции в виде ДНФ, а затем заменить все элементы построенной схемы на НЕ ИЛИ. Проиллюстрируем сказанное примером. Построим для выражения (3) двойственную функцию, представим ее в виде кратчайшей ДНФ:

.

Тогда исходная функция реализуется схемой рис. 3.8.

Рис. 3.8

Заметим, что при синтезе схем либо в базисе НЕ И, либо в базисе НЕ ИЛИ удобно воспользоваться кратчайшими или минимальными ДНФ, представляющими функцию или двойственную функцию.

В заключение этого раздела приведем пример синтеза n-разрядного сумматора.

Пусть слагаемые записаны в виде булевых векторов в регистрах X, Y, результат сложения представляется (n + 1)-разрядным регистром Z; , – переменные, сопоставляемые i-му разряду слагаемых; – переменная, сопоставляемая i-му разряду, представляющему сумму. Введем переменную для представления результатов переноса из i-го разряда в (i + 1)-й. Воспользовавшись введенными переменными, опишем работу двух блоков сумматора, формирующих результат сложения в i-м разряде сумматора, и перенос из i-го разряда в (i + 1)-й. Для i > 1 имеем

=   ,

=   .

Первая функция обращается в 1, когда нечетное число слагаемых, участвующих в формировании результата, принимают значение 1, что определяется операцией сложения по модулю два в двоичной системе счисления. Вторая функция обращается в 1, когда, по крайней мере, две из трех переменных принимают значение 1, что согласуется с условиями возникновения переноса в двоичной системе счисления.

Преобразуем первую функцию в ДНФ:

   .

В результате имеем совершенную ДНФ. Склеивание ее конъюнкций невозможно. Следовательно, совершенная ДНФ совпадает с сокращенной, из которой ни одна конъюнкция не может быть выброшена. Делаем заключение: полученная ДНФ является одновременно минимальной и кратчайшей.

Что касается ДНФ второго выражения, то ее конъюнкции не содержат отрицаний переменных, следовательно, это ДНФ сокращенная. Булева функция, представляющая перенос из i-го разряда в (i + 1)-й, является монотонной, следовательно, эта сокращенная ДНФ является одновременно минимальной и кратчайшей ДНФ.

Каждую из ДНФ реализуем отдельной одновыходной комбинационной подсхемой, например в базисе ДНФ. Блок-схема сумматора (рис. 3.9) представляет комбинационную схему с 2n входами и (n + 1) выходами.

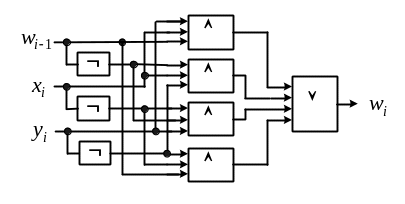
Рис. 3.9

КАДР