Арифметические действия в системах счисления с основанием, отличным от 10

Выполнение арифметических действий в любых позиционных системах счисления производится по тем же правилам, которые используются в десятичной системе счисления.

Так же, как и в десятичной системе счисления, для выполнения арифметических действий необходимо знать таблицы сложения (вычитания) и умножения. Ниже представлены данные таблицы для двоичной системы счисления

Таблица 1

Сложение	Вычитание	Умножение
0 + 0 = 0	0 – 0 = 0	0 ∙ 0 = 0
0 + 1 = 1	1 – 0 = 1	0 ∙ 1 = 0
1 + 0 = 1	1 – 1 = 0	1 ∙ 0 = 0
1 + 1 = 10	10 – 1 = 1	1 ∙ 1 = 1

Пользуясь приведенными таблицами, произведем арифметические операции над двоичными числами.

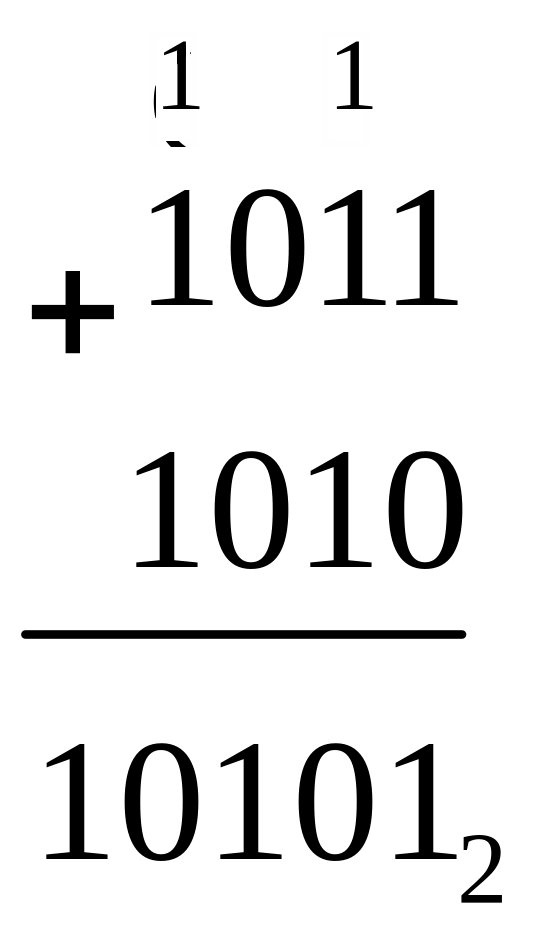
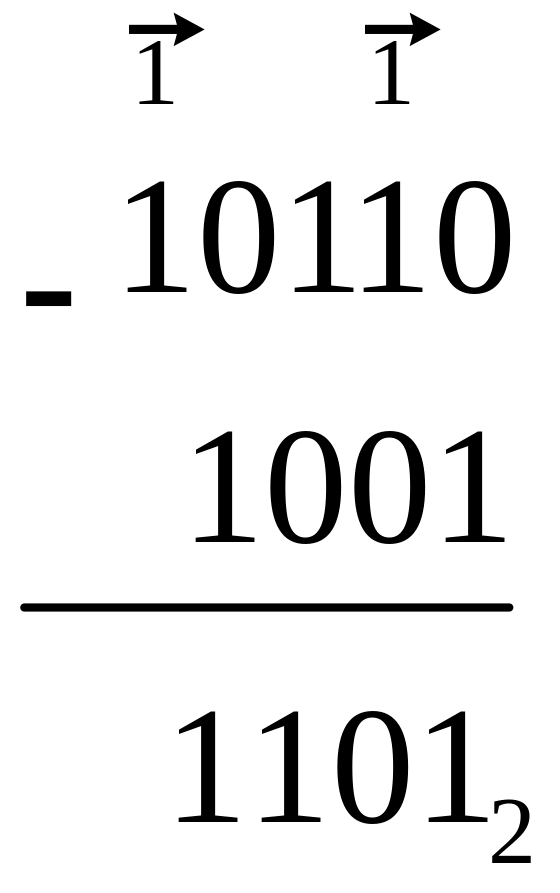
В тех случаях, когда занимается единица старшего разряда, она дает две единицы младшего разряда. Если занимается единица через несколько разрядов, то она дает единицы во всех промежуточных нулевых разрядах и две единицы в младшем нулевом разряде.

Рассмотрим операции умножения и деления двоичных чисел.

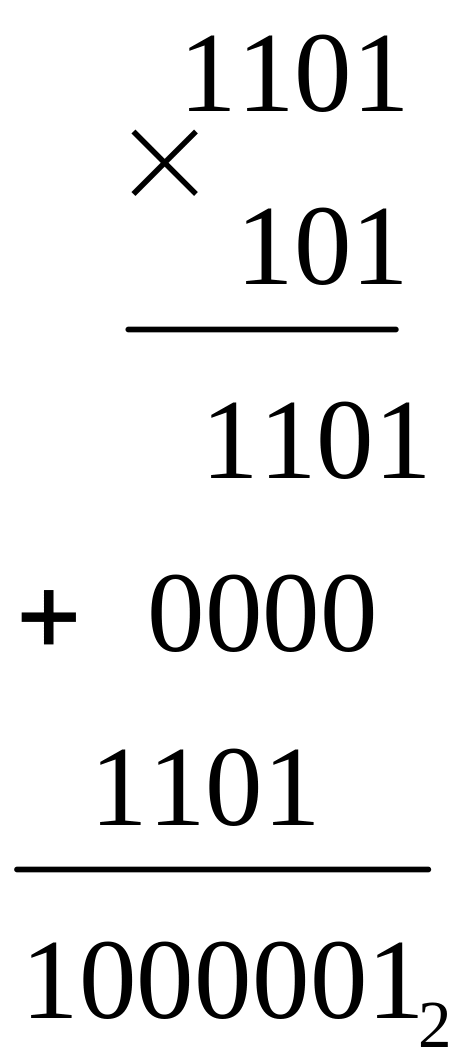
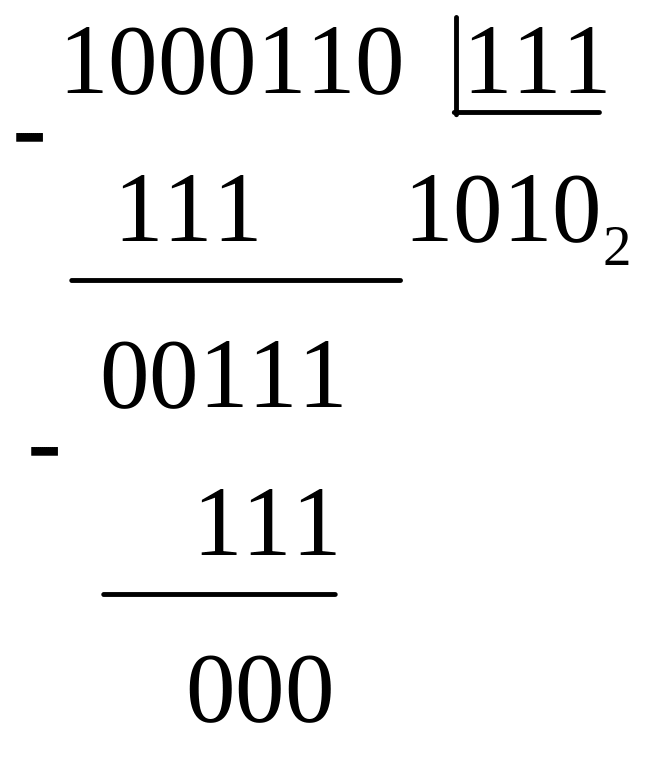
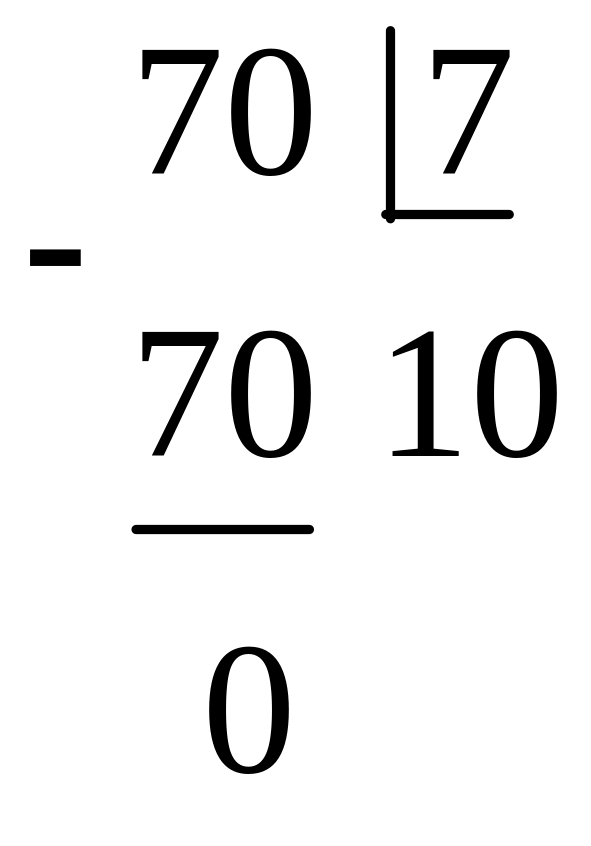
Зная операции двоичной арифметики, можно переводить числа из двоичной системы счисления в любую другую.

Пример: Перевести число 101111011₂ в десятичную систему счисления.

Поскольку 10₁₀ = 1010₂, запишем

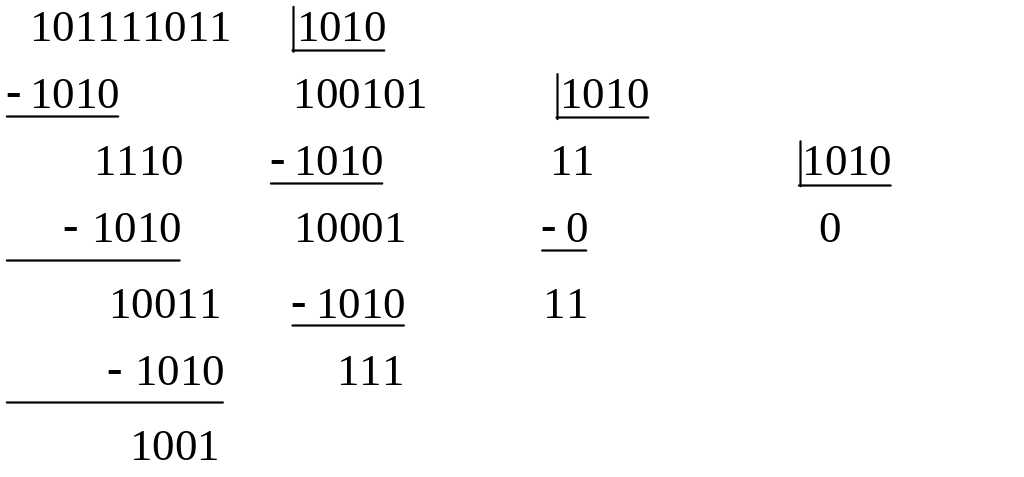
Полученные остатки, =1001₂ = 9₁₀, =111₂ = 7₁₀, =11₂ = 3₁₀. Искомое число 101111011₂ = 379₁₀.

В случае перевода чисел из одной недесятичной системы в другую возникает сложность выполнения действий в недесятичной системе счисления. В этом случае удобнее может быть делать перевод в два этапа m10q, где m и q – основания систем счисления соответственно.

Двоично-восьмеричные и двоично-шестнадцатеричные преобразования

Двоичная система счисления удобна для выполнения аппаратными средствами микропроцессора арифметических действий, но неудобна для восприятия человеком, поскольку требует много разрядов. Поэтому в вычислительной технике помимо двоичной системы счисления широкое применение нашли восьмеричная и шестнадцатеричная системы счисления.

Рассмотрим перевод чисел из двоичной системы счисления в восьмеричную.

Запишем число x в полиномиальной форме. Получим

Разделим обе части полученного выражения на 8. Учитывая, что 8 = 2³, получим

.

Таким образом, остаток от деления , что является двоичным разложением десятичного числа, лежащего в диапазоне [0; 7] (для изображения данной десятичной цифры в двоичной системе счисления требуется 3 разряда).

Таким образом, чтобы преобразовать двоичное число в восьмеричное, нужно объединить двоичные цифры в группы по 3 разряда справа налево. При необходимости в начале исходного числа нужно добавить незначащие нули. Затем каждая триада заменяется восьмеричной цифрой.

Пример: Преобразовать число 1101110₂ в восьмеричную систему счисления.

Объединяем двоичные цифры триады справа налево. Получаем

001 101 110₂ = 156₈.

Аналогичным образом производятся преобразования из двоичной системы счисления в шестнадцатеричную, только двоичные цифры объединяются в группы по 4 разряда (тетрады).

Пример: Преобразовать число 1101110₂ в шестнадцатеричную систему счисления.

Объединяем двоичные цифры триады справа налево. Получаем

0110 1110₂ = 6E₁₆.