
- •Министерство образования российской федерации
- •Казанский государственный энергетический университет
- •Элементы теории функций комплексноого переменного
- •Цель работы
- •Вид уравнения Тип числа ____ Множество:
- •Геометрическая интерпретация кч
- •Тригонометрическая форма кч
- •При перемножении и делении двух кч в тригонометрической форме
- •Используют тригонометрические формулы для суммы и разности двух углов и получают
- •Показательная форма кч
- •Области и линии на комплексной плоскости
- •Ряды с кч
- •Определение функции комплексной переменной
- •Элементарные функции комплексной переменной
- •Производная фкп
- •Конформное отображение
- •Криволинейный интеграл от фкп
- •Теорема Коши для односвязной области
- •Неопределенный интеграл от фкп
- •Основная теорема интегрального исчисления
- •Интегральная формула Коши
- •Бесконечные ряды
- •Нули функции
- •Ряд Лорана
- •Вычисление интегралов по формуле Коши
- •Теорема о вычетах
- •Вычисление вычетов
- •Определение порядка полюса
- •Вычисление интегралов
- •Устные экзаменационные вопросы
Вычисление вычетов
Пусть
f(z)
имеет полюс первого порядка. Тогда она
представляется в виде f(z)
=
![]() и рядом Лоранаf(z)
=
и рядом Лоранаf(z)
=
![]() .
Умножимf(z)
на (z
- a)
и перейдем к пределу
.
Умножимf(z)
на (z
- a)
и перейдем к пределу
![]()
lim
f(z)
(z
- a)
= lim![]() =
=![]() ( 49 )
( 49 )
т.е.
вычет функции с полюсом первого порядка
в точке а
равен пределу
произведения функции на множитель (z
- a)
при
![]() .
.
При вычислении предела в ( 49 ) используем правило Лопиталя
lim![]() =
lim
=
lim![]() =lim
=lim![]() =
=![]() =res
f(z)
(
50 )
=res
f(z)
(
50 )
т.е. для определения вычета достаточно значение числителя функции в точке а разделить на значение производной от знаменателя в этой точке.
Если f(z) имеет в точке а полюс порядка n, то разложение этой функции в ряд Лорана ( 46 ) умножим на (z - a)n
(z
- a)n
f(z)
=
![]() +
+![]() (z
- a)
+
…+
(z
- a)
+
…+![]() (z
- a)n
-1
+
(z
- a)n
(z
- a)n
-1
+
(z
- a)n
![]() ,
( 51 )
,
( 51 )
(n
- 1) раз продифференцируем и получим (n
- 1)!
![]() +
+
![]() .
.
Переход
к пределу
![]() исключает второе слагаемое и определит
вычет
исключает второе слагаемое и определит
вычет
![]() =
=
![]() ( 52 )
( 52 )
Пр.
Найти вычеты функции f
(z)
=
![]() .
.
Решение. Полюсами являются точки z = 1, z = 3 .
![]() =
=
![]() (z
- 1)
(z
- 1)
![]() =
=
![]()
![]() = -1/2
= -1/2
![]() =
=
![]() (z
- 3)
(z
- 3)
![]() =
=
![]()
![]() = 3/2
= 3/2
или
по формуле ( 47 ) :
![]() , тогда
, тогда
![]() =
=
![]() ,
,
![]() =
=
![]()
Пр.
Найти вычеты функции f(z)
=
![]() .
.
Решение. Здесь z = 2 - полюс третьего порядка, тогда по ( 52 ) имеем
![]() =
=
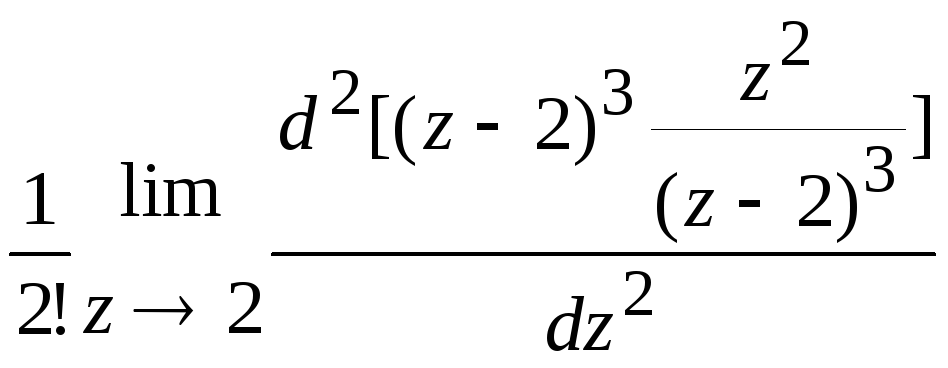 =
=![]()
Определение порядка полюса
Пусть f(z) имеет в точке а полюс порядка n и принимает вид
f(z)
=![]() +
+![]() +
. . . +
+
. . . +![]() +
+![]() (z).
(z).
Рассмотрим
![]() f(z),
где k
произвольно, и перейдем к пределу
f(z),
где k
произвольно, и перейдем к пределу
![]() . Приk
< n
получим
. Приk
< n
получим
![]() ,
при k
> n
получим 0
и только при
k
= n
получим
конечное число
,
при k
> n
получим 0
и только при
k
= n
получим
конечное число
![]() , т.е. условие
, т.е. условие
![]()
![]() (
53 )
(
53 )
определяет порядок полюса для f(z) в точке z = a путем подбора числа k .
Перейдем
к обратной функции
![]() .
Приz
= a
она обращается в 0 и её всегда можно
представить в виде
.
Приz
= a
она обращается в 0 и её всегда можно
представить в виде
![]()
=
![]() =
=![]()
где
![]() аналитическая функция и
аналитическая функция и![]() .
Числоn
определяет порядок
нуля для
.
Числоn
определяет порядок
нуля для
![]() приz
= a
и порядок полюса для f
(z).
Будем последовательно дифференцировать
приz
= a
и порядок полюса для f
(z).
Будем последовательно дифференцировать
![]() и переходить к пределу
и переходить к пределу![]() .
Первый не нулевой результат появится
только после вычисленияn
– ой производной. Таким образом, для
определения порядка полюса функции f
(z),
имеющей вид дроби, достаточно выполнить
одно из следующих действий : 1) представить
её знаменатель в виде
.
Первый не нулевой результат появится
только после вычисленияn
– ой производной. Таким образом, для
определения порядка полюса функции f
(z),
имеющей вид дроби, достаточно выполнить
одно из следующих действий : 1) представить
её знаменатель в виде
![]() ;
2) вычислять значения производных её
знаменателя до первого ненулевого
результата.
;
2) вычислять значения производных её
знаменателя до первого ненулевого
результата.
Пр.
![]() .
.
![]() f(z)
=
f(z)
=
![]() при
при![]() имеем полюс.
имеем полюс.
Определим его порядок. Первый способ: проведем разложение знаменателя в ряд
![]()
![]() нуль
2 порядка.
нуль
2 порядка.
Второй способ: определим порядок нуля знаменателя дифференцированием
![]() ,
,
![]()
![]()
Имеем полюс 2 порядка.
Пр. Определить тип особой точки z = 0 для функции
![]() .
.
Решение.
![]() f(z)=
f(z)=![]() .
Определим порядок нуля числителя и
знаменателя.
.
Определим порядок нуля числителя и
знаменателя.
![]() имеет
ноль 2 порядка (см. выше).
имеет
ноль 2 порядка (см. выше).
![]() =
=
![]() = 0,
= 0,
![]() =
=
![]() = 0,
= 0,
![]() =
=
![]() = 0,
= 0,
![]() =
=
![]() = 0,
= 0,
![]() =
=
![]() = 32
= 32
![]() имеем ноль 5 порядка.
имеем ноль 5 порядка.
![]() =
=
![]() ,
т.е. функцияf(z)
при
,
т.е. функцияf(z)
при
![]() имеет полюс 3 порядка.
имеет полюс 3 порядка.
Вычислим
производную от логарифма функции f(z)
=
![]()
![]() =
=![]()
![]() вычет производной дает порядок полюса
функции.
вычет производной дает порядок полюса
функции.
Вычисление интегралов
A)
Пр. Вычислить J
=![]()
![]() ,
если
,
если![]() -окружности:
1) |z
| = 1; 2)
| z
| = 3;
3)
| z
| = 5.
-окружности:
1) |z
| = 1; 2)
| z
| = 3;
3)
| z
| = 5.
Решение. Найдем вычеты относительно полюсов z = 0 , z = - 2 , z = - 4
![]()
 =
=
![]() z
f(z)
=
z
f(z)
=
![]()
![]() = 1/8
= 1/8
![]() =
=![]() (z
+ 2) f(z)
=
(z
+ 2) f(z)
=![]()
![]() = - ¼
= - ¼
![]() =
=
![]() (z
+ 4) f(z)
=
(z
+ 4) f(z)
=
![]()
![]() = 1/8
= 1/8
1)
Внутри окружности | z
| =1 находится
один полюс z
= 0
![]() J1=2
J1=2![]() i(
i(![]() )
=
)
=![]() i/4
i/4
2)
Внутри окружности | z
| = 3
находятся
полюсы z
= 0, z
=-2
![]()
J2
= 2![]() i(
i(![]() )
= -
)
= -![]() i
/ 4.
i
/ 4.
3)
Внутри окружности |
z
| = 5 находятся
полюсы z
= 0, z
=-2, z
=-4
![]() J3
= 2
J3
= 2![]() i(
i(![]() )
= 0 .
)
= 0 .
Б)
Рассмотрим
интегралы вида
![]() .
Здесь от действительной переменнойх
легко перейти
к комплексной переменной z.
Тогда интегрирование будет производиться
вдоль замкнутой окружности с учетом
теоремы о вычетах.
.
Здесь от действительной переменнойх
легко перейти
к комплексной переменной z.
Тогда интегрирование будет производиться
вдоль замкнутой окружности с учетом
теоремы о вычетах.
Пусть
а
= 0 и
![]() ,т.е.z
является комплексной переменной с
модулем r
= 1 и аргументом
х (
,т.е.z
является комплексной переменной с
модулем r
= 1 и аргументом
х (![]() .
Ей соответствует окружность |z
| = 1 . Тогда
.
Ей соответствует окружность |z
| = 1 . Тогда
![]()
![]()
![]() ;
;
![]() ;
;
![]() и
переходим к интегралу
и
переходим к интегралу
![]() .
Интервал
.
Интервал![]() приводит только к другой точке начала
движения по окружности.
приводит только к другой точке начала
движения по окружности.
Пр.
![]() .
Пусть
.
Пусть![]() ,
тогда
,
тогда![]() ,
,
![]() ,
,
![]() ,
,![]() =
=
=
=![]() .
Подынтегральная функция имеет две
изолированные особые точки, которые
являются полюсами 1 порядка. Но в
окружность радиуса 1 попадает только
полюс
.
Подынтегральная функция имеет две
изолированные особые точки, которые
являются полюсами 1 порядка. Но в
окружность радиуса 1 попадает только
полюс![]() и интеграл равен вычету в этой точке
и интеграл равен вычету в этой точке
 ,
,
![]() .
.
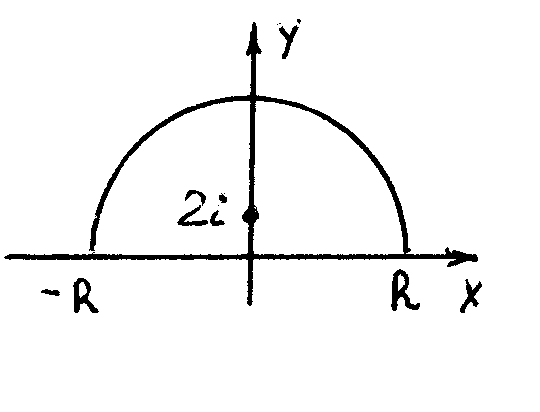
В)
Пусть f
(z)
аналитическая
функция в верхней полуплоскости, включая
действительную ось, за исключением m
полюсов ai
расположенных
над осью Ох.
Кроме того, lim
z2
f(z)
= C
– конечное
число при | z
|![]() ,
т.е. на
бесконечности функция становится
двукратной нулевой точкой (условие
Жордана). Построим замкнутый контур L,
состоящий из оси Ох
и полу-окружности радиуса R
,
т.е. на
бесконечности функция становится
двукратной нулевой точкой (условие
Жордана). Построим замкнутый контур L,
состоящий из оси Ох
и полу-окружности радиуса R![]() .
Тогда
.
Тогда
![]() =
=
![]() +
+
![]() , но
, но
в
силу условия Жордана
![]() = 0, и определенный интеграл от
функции
действительной
переменной
f(x)
будет
равен сумме
вычетов функции f
(z)
в ai
= 0, и определенный интеграл от
функции
действительной
переменной
f(x)
будет
равен сумме
вычетов функции f
(z)
в ai
J
=
![]() =
=
![]() (
54 )
(
54 )
Пр.
Вычислить J
=
![]()
![]() .
.
Решение.
Рассмотрим функцию f
(z)
=
![]() ,
аналитическую в верхней полуплоскости,
за исключением полюса 2 порядка в 2i.
Проверка
условия Жордана :
,
аналитическую в верхней полуплоскости,
за исключением полюса 2 порядка в 2i.
Проверка
условия Жордана :
![]()
![]() =
=
![]()
![]() =
=
![]()
![]() = { z
= r
eit
} =
= { z
= r
eit
} =
=
![]()
![]() =
0 , т.е. конечное число
=
0 , т.е. конечное число
![]() да.
да.
Вычисление вычета по формуле ( 52 )
![]() =
=![]()
![]()
![]() =
=![]()
![]()
![]() =
=![]()
![]() =
=![]()
Ответ.
J
= 2![]() i
i
![]() =
2
=
2![]() i
(
i
(![]() )
=
)
=
![]() .
.
