Функции комплексного переменного / пФКП

Казанский государственный энергетический университет

Кафедра «Высшей Математики»

ПРАКТИКУМ

по теме «Элементы теории функций комплексной переменной»

Методические указания к выполнению расчетного задания.

Опр. Комплексной функцией комплексной переменной (ФКП) наз. правило соответствия между элементами двух множеств, когда каждому значению переменной z = x + iy из множества D сопоставляется одно или несколько значений w = u + iv из множества W. D – область определения, W – область значений функции w = f(z).

Если w = u + i v есть функция от z = x + iy , то u и v являются действительными функциями от х, у и наоборот, всякое выражение w =u(x,y)+i v(x,y) есть ФКП от z =x + iy.

Геометрический смысл функция f(z) - отображать плоскость z в плоскость w . При этом линии и фигуры, описанные изменяющейся z , переходят в линии и фигуры совершенно другой конфигурации.

Задание 1 Дана функция f(z) = 3z³ – 2i, где z = x + i y. Найти её значение при z = 1 - i.

Решение.

f(1 – i) = 3(1³ – 3i + 3i² – i³) – i = - 2 – 3 i

Задание 2 Какие кривые заданы уравнением Re ( z² – 4z* ) = 5 ?

Пусть имеется равенство f(z) = a + ib . Оно сразу приводит к двум соотношениям Re f(z) = a и Im f(z) = b, которые связывают переменные х и у и, следовательно, определяют некоторые линии на координатной плоскости F₁(x,y) = 0 , F₂(x,y) = 0. В результате получаем комплексного представления кривых на плоскости .

Решение. z² – 4z* = (x + i y)² – 4(x – i y) = ( x² – y² – 4x ) + i ( 2xy + 4 ) ,

Re ( z² – 3z* ) = 5 x² – y² – 4x = 5 . Это уравнение кривой второго порядка. Приведем его к полному квадрату. ( x² – 2x2 + 4) – y² = 9 (x – 2)² – y² = 9

Получаем каноническое уравнение гиперболы с центром симметрии в точке (2;0) и полуосями a = b = 3 .

Задание 3 Является ли дифференцируемой функция f(z) = e^-x cos y - i e^-x sin y ?

Опр. Производная однозначной ФКП w = f(z) определяется как предел отношения приращения функции к приращению аргумента

lim = при ( 1 )

Если предел существует и не зависит от способа стремления к нулю, то функция

w = f(z) наз. аналитической в окрестности точки z .

Процесс определяют два процесса , и движение от точки z +z к точке z может происходить по произвольной кривой. Требование независимости

предела от способа стремления к нулю приводит к условиям Коши – Римана

, ( 2 )

Если ФКП w = u(x,y) + i v(x,y) можно представить как функцию одной независимой переменной z = x + iy, то она является аналитической за исключением отдельных точек. Это эквивалент условию Коши – Римана.

Решение.

1 способ. Проверка выполнения условий Коши – Римана: u = e^-x cos y, v = - e^-x sin y,

= - e^-x cos y, = - e^-x cos y да , = - e^-x sin y , = e^-x sin y да

2 способ. Представим f(z) как функцию одной переменной z . В таблице для элементарных функций находим e^z = e^x ( cos y + i sin y ) f(z) = e^-x cos y - i e^-x sin y = e^{- z}

Задание 4 Дана действительная часть функции u = x³– 3xy² + 1. Найти f(z), если f(0) = 1.

Функция u(x,y) должна быть гармонической, т.е. 6x = -(-6x). Общая идея: Вычисляем , . Эти производные по условиям Коши-Римана меняем на ,. Полученные дифференциальные уравнения интегрируем и находим v(x,y).

Решение. Вычислим = - 6xy . Заменим по условию Коши-Римана на - . Проинтегрируем дифференциальное уравнение = 6xy dv = 6xy dx v(x,y) = 3yx² + h(y), где h(y) - произвольная функция у. Вычислим = 3x² + h`(y) . Заменим по условию Коши –Римана на : = 3x<sup>2</sup> + h`(y) , но

= ( x³ – 3xy² + 1) = 3x² – 3y² . Сравнение производных дает h`(y) = – 3y² или dh = – 3y²dy h(y) = - y³ + C или v(x,y) = 3yx² – y³ + C .

Ответ. f(z) = (x³ – 3xy² + 1) + i(3yx² – y³) + C = (x + iy)³ + 1 + C = z³ + C

Условие f(0) = 1 определяет константу C = 1 .

Задание 5 Вычислить интегралы:

а) J = (z² + 1) dz , где АВC – ломаная, z_A = 0, z_B = -1+ i , z_C = i .

б) J = z|z| dz , где L : |z| = 1, Im z > 0

а) Решение. Способ 1 Общая формула J = u dx – v dy + iv dx + u dy ( 3 )

f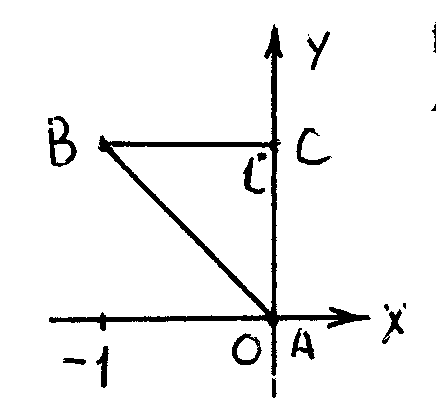(z) = (x + iy)² + 1 = (x² - y² + 1) + i(2xy), АВС = АВ + ВС

АВ: y = -x, dy = -dx, 0x-1, u = 1 , v = - 2x²

J_АВ = = -1/3 + 5i/3

BC: y = 1, dy = 0, -1x0 , u = x² , v = 2x

J_BC = = 1/3 – i , J = J_АВ + J_BC = 2i/3

Способ 2 По формуле Ньютона-Лейбница f(z) dz = F(b) - F(a) ( 4 )

J = = []|₀ⁱ = 2i/3

б) Решение. Способ 1 Общая формула: J = u dx – v dy + iv dx + u dy ( 3 ) f(z) = z|z| = (x + iy)= x + i y

L: x² + y² = 1 y = , dy =, 1x-1, u = x, v = y

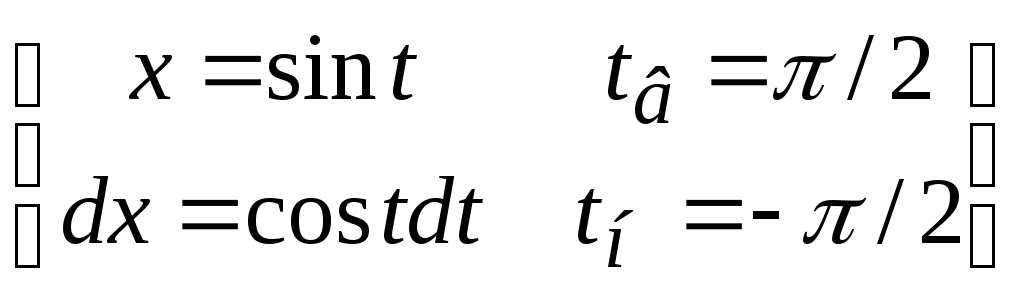J = - + i { + } = 0 + i =

= = i = i =

= i ½ sin 2t = 0

Способ 2 Представим z в показательной форме z = re^it _, тогда dz = e^itdr + ir e^itdt ( 5 )

L: |z| = 1, Im z > 0 r = 1 , dr = 0 , ,

J = z|z| dz = = ½ i = ½ i(cos 2t + isin 2t) = 0

Задание 6 Разложить в ряд Лорана по степеням z функцию f(z) =

Решение. Представим дробь в виде суммы простейших дробей

= = - []

и приведем их к общему знаменателю

A(z² – 5z – 50) + Bz(z² – 5z – 50) + C z²(z – 10) + D z²(z + 5) = -(5z + 100)

z³ | B + C + D = 0 A = 2

z² | A - 5B – 10C + 5D = 0 Решение системы B = - 0,1

z¹ | -5A – 50B = -5 линейных уравнений: C = 0,2

z⁰ | -50A = -100 D = - 0,1

f(z) = =

Имеем суммы двух геометрических прогрессий , с q = -z/5, q = z/10

f(z) = - 0,04 - 0,01.

Из условий сходимости |-z/5| < 1 , |z/10| < 1 |z| < 5 , |z| < 10 .

Ответ: Функция f(z) имеет полюс 2 порядка в точке z = 0 и определена в круге 0 < R< 5 . Вычет функции, т.е. коэффициент А _-1 при 1/z , равен 0,1 .

Задание 7 Вычислить интеграл J = , где L : | z | = 2

Решение. Функция f(z) имеет точки разрыва при z = 0 , z = . Т.к. sin x x при малых х, то эти точки являются полюсами 1 порядка. В круг радиуса R = попадает только один полюс z = 0 и интеграл равен вычету A _-1 в этом полюсе

J =f(z) dz = 2i A _-1 = () ( 6 )

Если а полюс 1 порядка, то вычет А _-1 = lim f(z)(z – a) при za ( 7 )

A _-1 = = z = = , т.к. = 1

Задание 8a Вычислить интеграл J = dz , где L : | z | = 1

Решение 1. Функция f(z) при z = 0 имеет неопределенное значение {0/0}. Определим порядок полюса. Общая формула: функция f(z) имеет полюс порядка k в точке а,

если при za lim (z – a)^k f(z) = c – конечное число ( 8 )

Пусть k = 1, тогда при z0 lim z f(z) = lim = lim = ½ lim= ½ ,

т.е. имеем полюс порядок 1 и по ( 7 ) А _-1 = ½ . Полюс z = 0 попадает в круг R 1, и интеграл равен вычету в этом полюсе

J =f(z) dz = 2i A _-1 = (i)

Решение 2. Функцию f(z) представим в виде ряда по степеням z

f(z) = =[-1 + 1 -+ - . . . ] = ½ + . . . A _-1 = ½

Задание 8b Вычислить интеграл J = dz , где L : | z | = 1/3 .

Решение 1. Общая формула для вычисления вычета в полюсе порядка n в точке а

res f(z) = lim при z a ( 9 )

В нашем случае функция f(z) имеет полюс 2 порядка при z = 0

A _-1 = = == -1

Полюс z = 0 попадает в круг R1/3 и интеграл равен вычету в этом полюсе

J =f(z) dz = 2i A_-1 = -2i

Решение 2. Представим f(z) в виде разложения по степеням z

f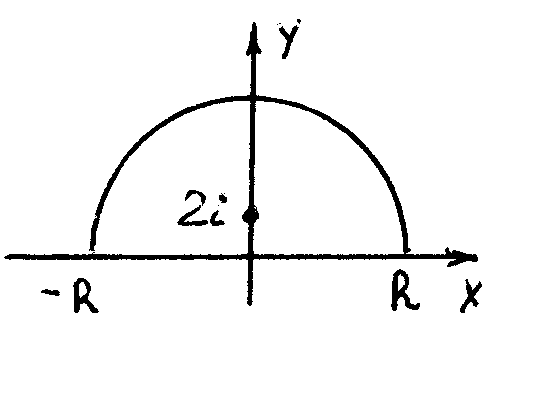(z) = = ½ - + A _-1 = -1

Задание 9 Вычислить несобственный интеграл J = .

Решение. Функция f(x) = = аналити-

ческая в верхней полуплоскости, за исключением полюса 3 порядка в точке 2i . Проверка условия Жордана: lim z²f(z) = c – конечное число при |z| (10 )

lim z²f(z) = lim = lim = { z = r e^it } =

= lim= 0 (да) интеграл равен вычету в точке z = 2i.

Вычислим 2-ю производную от функции [(z – 2i)³ f(z)] == (z + 2i)^-3,

[(z + 2i)^-3]` = -3(z + 2i)<sup>-4</sup>, [-3(z + 2i)<sup>-4</sup>]` = 12(z + 2i)^-5 и найдем вычет по формуле ( 9 )

A _-1 = == . Ответ: J = = 2i A _-1 =

4