2.8.4 Подготовка к работе

Самостоятельная подготовка студентов к выполнению лабораторной работы осуществляется по следующим разделам:

– моделирование электропотенциального поля в проводящей среде [15];

– основы теории подобия [1, 2];

– математическое моделирование [8];

2.8.5 Вопросы для самопроверки

1 Требования к материалу электродов и электролитов.

2 Назовите особенности моделирующих устройств.

3 Что представляют собой модели прямой аналогии?

4 Расскажите о методах электрического моделирования полей.

5 Расскажите о моделировании тепловых систем.

6 Преимущества и недостатки моделей на основе жидких проводящих сред.

7 Что используют в качестве измерительных устройств в моделирующих установках?

2.8.6 Порядок выполнения работы

2.8.6.1 Используя экспериментальные данные, полученные при моделировании электропотенциального поля в проводящей среде (Приложение Б), найти пересечения эквипотенциальных поверхностей , соответствующих варианту задания из таблицы 2, с осями х, у и радиусом , проходящим под углом к вышеуказанным осям.

2.8.6.2 Построить графики сечений заданных поверхностей .

Таблица 2 – Варианты заданий

Вариант задания	Значения разностей потенциалов, В
1	0,640	0,091	0,185
2	0,620	0,080	0,177
3	0,580	0,090	0,165
4	0,560	0,123	0,073
5	0,540	0,200	0,088

2.8.6.3 Расчет выполнить следующим образом.

Для построения сечений заданных по экспериментальным данным эквипотенциальных поверхностей необходимо найти их точки переcечения с осями х, у и радиусом .

Для построения экспериментальной кривой, соответствующей значению , предположим, что распределение разности потенциалов по оси х от точки с координатами (10; 1) при до точки (15; 1) при описывается квадратичной функцией вида

. (1)

При подстановке значений , и соответствующих им разностей потенциалов в выражение (1), получаем систему уравнений с коэффициентами a и b

. (2)

Решая систему уравнений (2), находим значения коэффициентов

и . (3)

При этом выражение (1) с учетом коэффициентов а и b принимает вид

. (4)

Для значения получаем квадратное уравнение:

, (5)

решая которое, находим требуемый корень уравнения . Следовательно, экспериментальная эквипотенциальная кривая пересекает ось х в точке с координатами .

Аналогично распределение разности потенциалов по оси у от точки с координатами (0; 10) при до точки при описывается квадратичной функцией

. (6)

При подстановке значений , и соответствующих им значений разностей потенциалов в выражение (6) получаем систему уравнений

. (7)

Решая систему уравнений (7), находим коэффициенты

и . (8)

Следовательно, экспериментальное распределение по оси у с учетом (6) и (8) принимает вид

. (9)

Для значения получаем квадратное уравнение

. (10)

Решая (10), находим требуемый корень уравнения . Следовательно, пересечение экспериментальной эквипотенциальной кривой с осью – в точке с координатами .

Далее необходимо определить пересечение экспериментальной кривой с радиусом , проходящим под углом к осям х и у. Предположим, что распределение разностей потенциалов от точки с координатами, определяемой радиусом при к точке , соответствующей радиусу при также описывается квадратичной функцией вида

. (11)

При этом распределение разности потенциалов осуществляется от радиуса до радиуса . При подстановке указанных радиусов и соответствующих им значений разностей потенциалов в выражение (11), получаем систему уравнений

. (12)

Решая систему уравнений (12), находим коэффициенты

и . (13)

Выражение (11) с учетом значений (13) принимает вид

. (14)

При получаем квадратное уравнение:

, (15)

при решении которого находим требуемый корень уравнения .

Таким образом, пересечение экспериментальной эквипотенциальной поверхности с определяется радиусом со значением .

Аналогичным образом, с использованием выражений ( ) были получены точки пересечения поверхностей и с осями х, у и радиусом . Полученные координаты точек для всех трех эквипотенциальных поверхностей представлены в таблице 3.

Таблица 3 – Координаты точек пересечения экспериментальных

эквипотенциальных поверхностей с осями х, у и радиусом

Значения разностей потенциалов , В
Точки пересечения эквипотенциальных поверхностей с	осью х, мм	(10,7; 0)
	осью у, мм	(0; 12,1)
	радиусом , мм	12,3

По полученным данным на рисунке 7 построен график сечения экспериментальной эквипотенциальной поверхности, соответствующей значению .

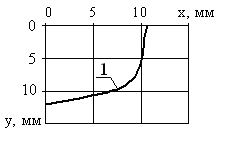
Рисунок 7 – Сечение экспериментальной эквипотенциальной

поверхности, соответствующей значению (1)