
Геометрические преобразования
При работе с графическими системами и формировании изображения постоянно возникает необходимость его изменить. В распоряжении пользователя находится большой арсенал команд редактирования: перемещение, поворот, осевая симметрия, подобие, копирование, изменение размеров объекта и многие другие.
Двумерные преобразования
В основе изменения графической информации лежат три основных преобразования: перенос, масштабирование и поворот. На их основе строятся все известные изменения объектов в графических системах.
Перенос
Точки на плоскости можно перенести в новые позиции путем добавления к координатам этих точек констант переноса. Для каждой точки Р(х, у), которая перемещается в новую точку Р'(х',у') сдвигаясь на Dx единиц по оси X и на Dy по оси Y. можно написать

Но объект представляет собой множество точек. Его можно переносить, применяя уравнение переноса к каждой точке. Однако каждый отрезок состоит из бесконечного числа точек, и этот процесс длился бы бесконечно долго. Удобнее перенести все точки, принадлежащие отрезку, путем перемещения одних лишь крайних его точек, а затем вычертить новый отрезок между ними (рис. 2.1).

Масштабирование
Точки можно масштабировать (растянуть) в Sx раз по оси X и в Sy раз по оси Y. Получим новые точки с помощью умножения:
x’ = x*Sx,y’ = y*Sy
Определить S в виде матрицы:
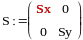 ,
,
м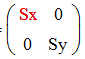
 ожно
записать в матричной форме:
ожно
записать в матричной форме:
[x’y’] = [xy] *
или
P’ = P*S.
М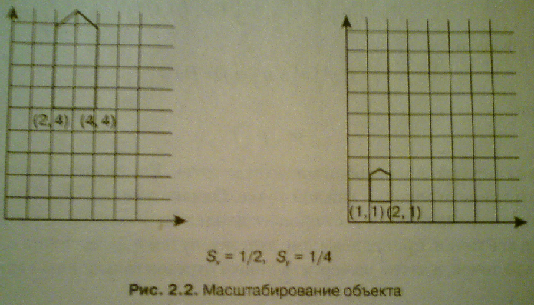 асштабирование
производится относительно начала
координат (рис. 2.2).
В
результате домик стал меньше и ближе к
началу координат. Если бы масштабные
коэффициенты были больше единицы, домик
увеличился бы и отдалился от начала
координат. Пропорции домика тоже
изменились. Было применено неоднородное
масштабирование, при котором Sx
≠ Sy.
Однородное масштабирование (Sx
= Sy
) не влияет на пропорции.
асштабирование
производится относительно начала
координат (рис. 2.2).
В
результате домик стал меньше и ближе к
началу координат. Если бы масштабные
коэффициенты были больше единицы, домик
увеличился бы и отдалился от начала
координат. Пропорции домика тоже
изменились. Было применено неоднородное
масштабирование, при котором Sx
≠ Sy.
Однородное масштабирование (Sx
= Sy
) не влияет на пропорции.
Поворот
Т очки
могут быть повернуты на угол α относительно
начала координат (рис. 2.3).
очки
могут быть повернуты на угол α относительно
начала координат (рис. 2.3).
Тогда координаты точки Р':
x’ = xcosΘ – ysinΘ,
y’ = xsinΘ + ycosΘ
В матричной форме:

или P’ = P*R , где R — матрица поворота.
П оложительное
значение соответствует повороту против
часовой стрелки (рис. 2.4), отрицательное
— по часовой стрелке.
оложительное
значение соответствует повороту против
часовой стрелки (рис. 2.4), отрицательное
— по часовой стрелке.
Рис. 2.4. Поворот объекта
О
Преобразования переноса, масштабирования и поворота в матричной форме имеют вид:
P’ = P + T
P’ = P*S
P’ = P*R
Перенос реализуется с помощью операции сложения, а масштабирование и поворот — с помощью умножения. Это вызывает неудобство при осуществлении нескольких преобразований над объектом. Каждую точку объекта придется последовательно подвергать каждому преобразованию. Если объект имеет N точек и необходимо провести, например, три последовательных преобразования, то понадобится 3 * N действий. Удобно было бы все преобразования представить в единой форме. Тогда можно было бы один раз найти результирующую матрицу преобразования, а затем лишь умножить ее на все точки. В таком случае количество действий стало бы N + 2, где 2 — это две операции по умножению трех матриц. Если выразить точки в однородных координатах, то все три преобразования можно реализовать с помощью операции умножения. И хотя умножение выполняется аппаратно медленнее сложения, и размерность матриц увеличивается на единицу, при большом количестве точек объекта наблюдается ощутимое преимущество.
В однородных координатах точка Р(х, у) записывается как Р( W*х, W*у,W), где W— масштабный множитель, не равный нулю.
При этом если точка задана в однородных координатах Р(Х, Y,W), то можно найти ее декартовы координаты:
X
=
 ,
Y
=
,
Y
=
 .
.
Если же W = 1, то операция деления не нужна:
P(x,y,1) , P’(x’,y’,1)
Основные преобразования в однородных координатах выразятся следующим образом.
Перенос
У равнение
переноса запишется в виде матрицы
преобразования:
равнение
переноса запишется в виде матрицы
преобразования:
1 0 0
[x’ y’ 1] = [x y 1] * 0 1 0
Dx Dy 1
Или P’ = P * T (Dx , Dy), где
П еремножив,
получим:
еремножив,
получим:
[x’ y’ 1] = [x + Dx , y + Dy , 1].
То есть перенос – функция аддитивная.
М асштабирование
/
[x’ y’ 1] = [x y 1] *
Уравнение масштабирования в матричной форме имеет вид:
О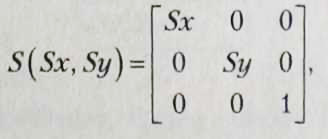 пределяя
пределяя
имеем:
P’ =P*S(Sx,Sy)
Перемножив, получим:
[x’ y’ 1] = [x*Sxy*Sy1].
Докажем
что масштабирование – функция
мультипликативная, то есть если точку
P(x,y)
промасштабировать в точку P’(x’,y’)
c
S=
(Sx1,Sy1),
а потом – в точку P’’(x’’,y’’)
c
S=(Sx2,Sy2),
то результат будет иметь вид:
S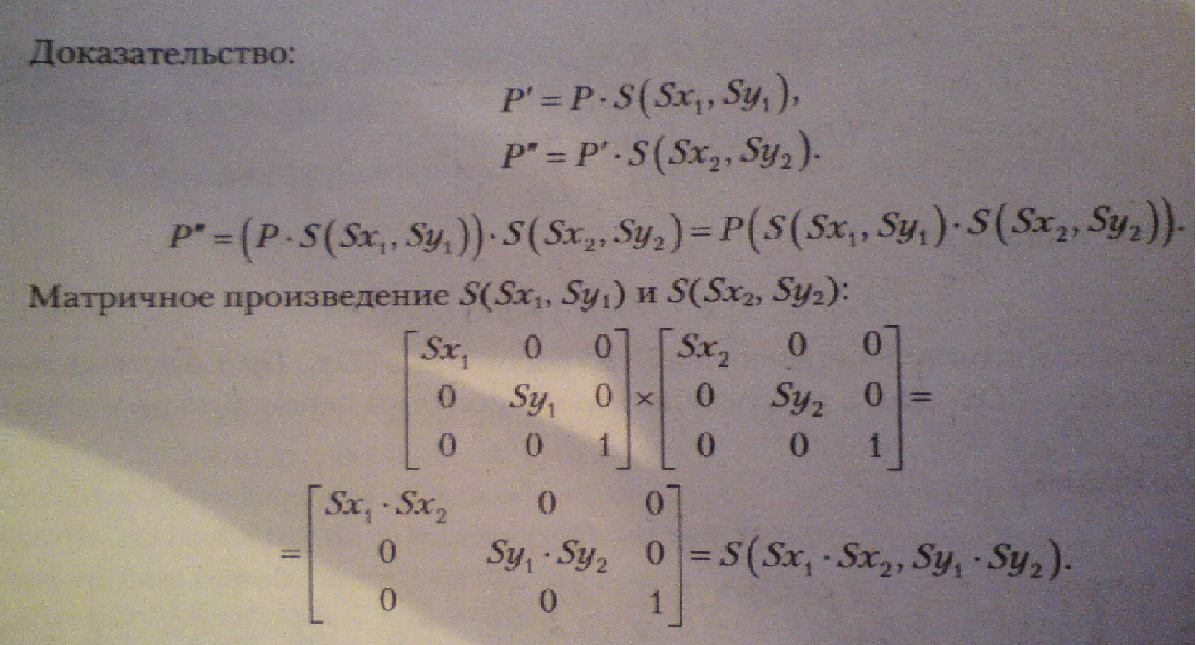 =(Sx1*Sx2*Sy1*Sy2).
=(Sx1*Sx2*Sy1*Sy2).
С помощью масштабирования легко реализуется
осевая симметрия. Для этого используется
отрицательные значения коэффициентов
масштабирования в матрице.
помощью масштабирования легко реализуется
осевая симметрия. Для этого используется
отрицательные значения коэффициентов
масштабирования в матрице.
Поворот
