4.4. Потери в катушках индуктивности

В катушках индуктивности помимо основного эффекта взаимодействия тока и магнитного поля наблюдаются паразитные эффекты, вследствие которых сопротивление катушки не является чисто реактивным и равным Х_L. Наличие паразитных эффектов ведет к появлению потерь в катушке, оцениваемых сопротивлением потерь R_П, которое определяет добротность катушки индуктивности

Q = .

(4.10)

Потери складываются из потерь в проводах, диэлектрике, сердечнике и экране.

Потери в проводах вызваны тремя причинами.

Во-первых, провода обмотки обладают омическим сопротивлением

,

(4.11)

где l – длина провода обмотки; d – диаметр провода; ρ – удельное сопротивление.

Это сопротивление (Ом) можно выразить через число витков w и средний диаметр катушки Dср_,

где Dср = – диаметр провода в см.

	(4.12)

Во-вторых, сопротивление провода обмотки переменному току возрастает с ростом частоты, что обусловлено поверхностным эффектом, суть которого состоит в том, что ток протекает не по всему сечению проводника, а по кольцевой части поперечного сечения (рисунок 4.6), ширина (мм) которой равна

,

(4.13)

г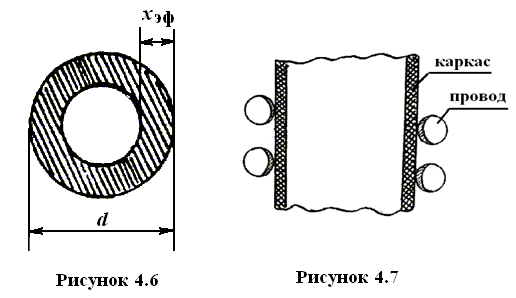 де f – частота в МГц; – удельное сопротивление в мкОм·м.

Вследствие этого провод длиной l имеет сопротивление переменному току равное

,

(4.14)

где S_ЭФ – площадь кольца, которая равна

,

(4.15)

где .

После преобразования получаем

.

(4.16)

В третьих, в проводах обмотки, свитой в спираль, проявляется эффект близости (рисунок 4.7), суть которого состоит в вытеснении тока под воздействием вихревых токов и магнитного поля к периферии провода, прилегающей к каркасу, в результате чего сечение, по которому протекает ток, принимает серповидный характер, что ведет к дополнительному возрастанию сопротивления провода.

Сопротивление r_Б, обусловленное эффектом близости, прямо пропорционально диаметру провода, а сопротивление r_П, обусловленное эффектом, обратно пропорционально диаметру провода (рисунок 4.8).

Существует оптимальный диаметр провода dопт, при котором сопротивление провода току высокой частоты r_f = r_Б + r_П оказывается минимальным. Для однослойных катушек dопт = 0,2…0,6мм, для многослойных dопт = 0,08…0,2мм. Существенно уменьшить потери в проводах можно применяя

провод "литцендрат", состоящий из большего числа жилок, скрученных в жгут. При небольшом диаметре тонких жилок ослабляется поверхностный эффект, а скручивание жилок в жгут ослабляет эффект близости.

Существует методика расчета сопротивления r_f , по которой предварительно рассчитывается вспомогательный коэффициент

,

(4.17)

где f - частота в Гц; d- диаметр провода в см.

Затем по таблице 4.1 находятся коэффициенты F(z) и G(z).

Таблица 4.1

Z	F(z)	G(z)
0,5	1	0,001
0,6	1	0,002
0,7	1	0,004
0,8	1	0,006
0,9	1	0,01
1	1,01	0,015
1,5	1,03	0,07
2	1,08	0,17
2,5	1,18	0,3
3	1,3	0,4
4	1,7	0,6
5	2	0,8
7,5	2,9	1,2
10	3,8	1,6
20	7,3	3,4
25	9,1	4,3
50	18	8,2
100	36	18

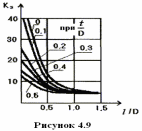
После этого по графику (рисунку 4.9) определяется вспомогательный коэффициент Кз, зависящий от геометрии катушки.

По (4.18) рассчитывается сопротивление провода катушки току высокой частоты

,

(4.18)

г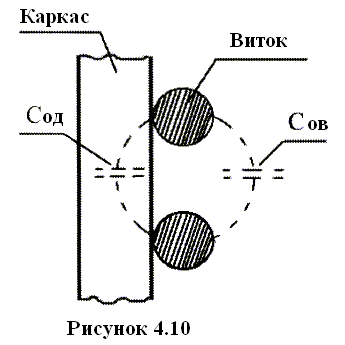 де D – наружный диаметр катушки в см; d – диаметр провода в см.

Если однослойная катушка намотана проводом оптимального диаметра и параметр z > 5, то сопротивление r_f можно определить по формуле

,

(4.19)

где D – в см;  d – в см, f' – в МГц.

Потери в диэлектрике обусловлены тем, что между соседними витками катушки существует емкость, имеющая две составляющих. Ёмкость через воздух С_ов и емкость через диэлектрик С_од (рисунок 4.10).

Потери в диэлектрике учитываются величиной tg, зная которую можно рассчитать сопротивление потерь

rД   = 0,250Сод tgL2f 3 . 10-6

(4.20)

где  С_од – в пф; L – в мкГн,  f – в МГц.

Потери в сердечнике складываются из потерь на вихревые токи _в, потерь на гистерезис _г и начальных потерь _п и учитываются как тангенс угла потерь в сердечнике

tgс = в ·f + г·Н + п

(4.21)

В справочниках приводятся значения. tg_с  для различных типов сердечников. Сопротивление потерь определяется по формуле

rc = tgсL

(4.22)

Таким образом суммарное сопротивление потерь в катушке индуктивности, определяющее ее добротность, равно

Rп = rf + rд +rc

(4.24)

П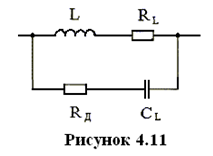 рактически величина добротности лежит в пределах от 30 до 200. Повышение добротности достигается оптимальным выбором диаметра провода, увеличением размеров катушки индуктивности и применением сердечников с высокой магнитной проницаемостью и малыми потерями.

С учетом потерь и паразитной емкости катушку индуктивности можно представить в виде эквивалентной схемы (рисунке 4.11), где  R_п = r_f + r_д + r_c. Добротность катушки Q = L/R_п  зависят от температуры. Зависимость Q от температуры определяется температурным коэффициентом добротности ТКД=Q/QТ
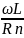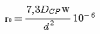
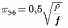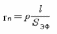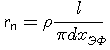
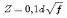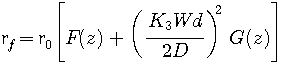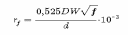