
- •Лабораторная работа № 2 Разработка имитационных моделей для исследования вероятностных распределений и их числовых характеристик
- •Моделирование дискретных случайных величин
- •Моделирование непрерывных случайных величин
- •Числовые характеристики вероятностных распределений
- •Проверка адекватности моделей
- •Задание
- •Порядок выполнения лабораторной работы
Лабораторная работа № 2 Разработка имитационных моделей для исследования вероятностных распределений и их числовых характеристик
Цель лабораторной работы: приобретение практических навыков разработки имитационных моделей для исследования вероятностных распределений и их числовых характеристик
Краткие теоретические сведения
Пусть R есть случайная величина с функцией распределения F(x) = P( < x) , являющаяся математической моделью единичного наблюдения одной из компонент или одного из показателей, используемых в ходе имитационного эксперимента.
Наибольшее распространение на практике имеют два класса функций распределения F(x) :
абсолютно-непрерывные
дискретные.
В первом случае существует плотность распределения вероятностей случайной величины :
![]() .
(1)
.
(1)
Во втором случае случайная величина принимает значения из дискретного множества A = (a1, a2, ... , ak), a1 < a2 , ... < ak, k и имеет дискретное распределение вероятностей:
![]() .
(2)
.
(2)
Моделирование дискретных случайных величин
Для моделирования дискретных случайных величин на практике используются распределения:
Распределение Бернулли:
![]() .
(3)
.
(3)
Биноминальное распределение:
![]() .
(4)
.
(4)
Геометрическое распределение:
![]() .
(5)
.
(5)
Отрицательное биноминальное распределение:
![]() .
(6)
.
(6)
Гипергеометрическое распределение:
 .
(7)
.
(7)
Распределение Пуассона:
![]() .
(8)
.
(8)
Дискретное равномерное распределение:
![]() .
(9)
.
(9)
Дискретная случайная величина принимает N < заданных значений С0, С1, ... , СN-1 с вероятностями р0, р1, ... , рN-1. Количественную оценку точности моделирования дискретных случайных величин позволяет получить график эмпирических и теоретических частот.
Моделирование непрерывных случайных величин
Для моделирования непрерывных случайных величин с плотностью вероятностей f(x) на практике наиболее часто используются 14 распределений:
Равномерное распределение на отрезке a, b:
![]() . (10)
. (10)
Нормальное (гауссовское) распределение:
 (11)
(11)
3. Экспоненциальное распределение:
![]() .
(12)
.
(12)
Распределение Лапласа:
![]() .
(13)
.
(13)
Логистическое распределение:
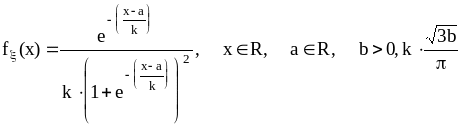 .
(14)
.
(14)
Гамма-распределение:
 .
(15)
.
(15)
Г() - гамма-функция.
Распределение Вейбулла-Гнеденко:
![]() .
(16)
.
(16)
Бетта-распределение:
![]() .
(17)
.
(17)
Хи-квадрат распределение:
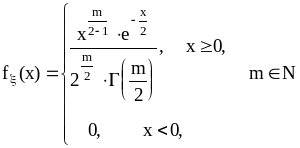 . (18)
. (18)
Распределение Фишера:
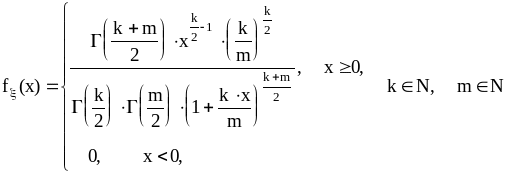 .
(19)
.
(19)
Распределение Стьюдента:
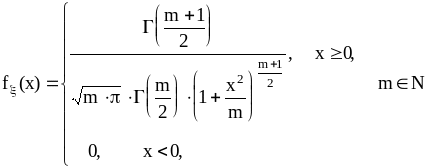 .
(20)
.
(20)
Распределение Коши:
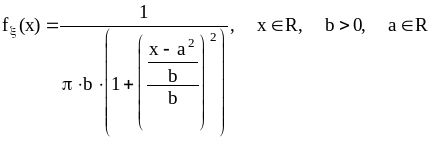 .
(21)
.
(21)
Логнормальное распределение:
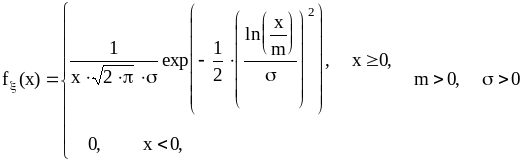 .
(22)
.
(22)
Смесь двух нормальных распределений:
![]() .
(23)
.
(23)
По выборке реализаций непрерывной случайной величины строятся график значений случайной величины и гистограмма, которые можно использовать для качественной оценки точности моделирования непрерывных случайных величин.
