Федеральное агентство по образованию

Воронежский государственный университет

Mатематическая статистика

Учебно-методическое пособие

по специальности 071900 «Информационные системы и технологии»

для студентов 2 курса очной формы обучения

Воронеж – 2011

Оглавление

1. Основные понятия…………………………………………………………………………2

2. Статистические оценки параметров распределения…………………………………….5

3. Метод моментов …………………………………………………………………………...6

4. Метод максимального правдоподобия……………………………………………………8

5. Интервальные оценки…………………………………………………………………….10

6. Вероятностные распределения, применяемые в статистике: гамма-распределение, распределение 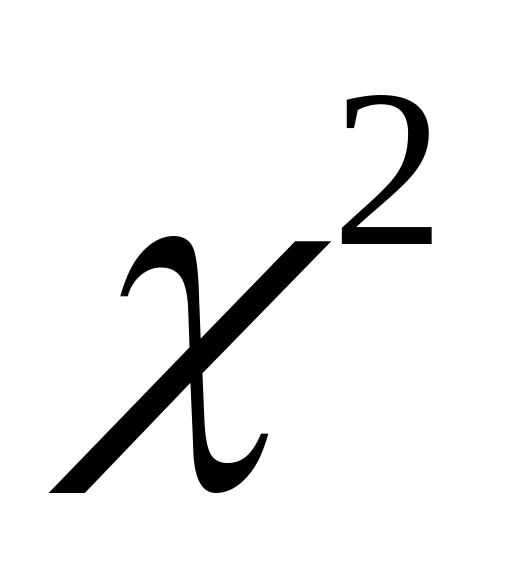, распределение Стьюдента………………………………………….12

7. Критерий согласия …………………………………………………………………….16

§ 1. Основные понятия

СПРАВОЧНЫЕ СВЕДЕНИЯ

1. Предмет, задачи математической статистики. Основные понятия

Предмет. Математической статистикой называется наука, занимающаяся методами обработки опытных данных, полученных в результате наблюдений над случайными явлениями.

Задачи. Упорядочение статистического материала, представление его в наиболее удобном для обозрения и анализа виде. Оценка вероятностных характеристик случайной величины, над которой велись наблюдения, а также проверка вероятностных гипотез.

Статистическое распределение выборки. Статистическим распределением выборки называют перечень наблюдавшихся значений признака , записанных в возрастающем порядке, и соответствующих им частот

(сумма всех частот равна объему выборки ) или относительных частот (в качестве частоты интервала принимают сумму частот наблюдавшихся значений, попавших в этот интервал).

Эмпирическая функция распределения. Эмпирической функцией распределения называют функцию , определяющую для каждого значения относительную частоту события

где - число наблюдавшихся значений, меньших , -объем выборки.

Эмпирическая функция распределения обладает следующими свойствами:

1. Значения эмпирической функции распределения принадлежат отрезку .

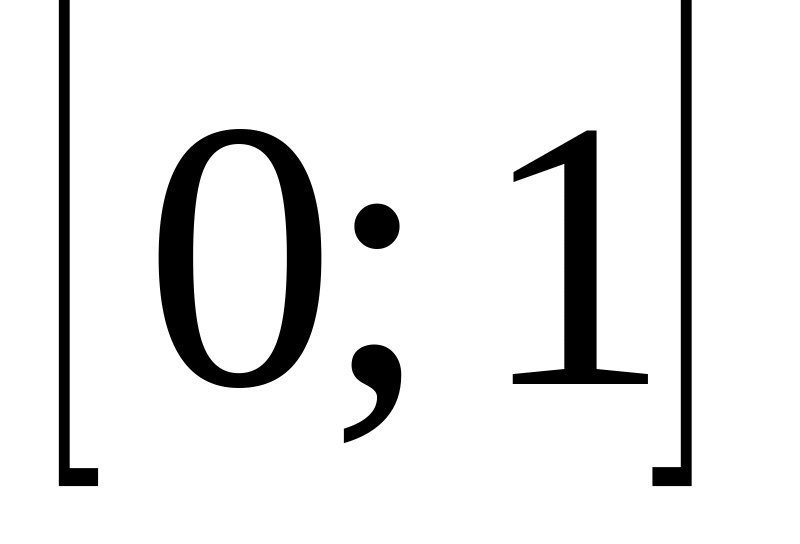2. Эмпирическая функция распределения является неубывающей функцией.

3. Эмпирическая функция распределения равна нулю левее наименьшего наблюденного значения и единицы – правее наибольшего.

Гистограмма. Гистограммой частот (статистический аналог кривой распределения) называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длины , а высоты равны отношению (плотность частоты). Площадь частичного -го прямоугольника равна - сумме частот вариант, попавших в -й интервал. Площадь гистограммы частот равна сумме всех частот, т.е. объему выборки .

Гистограммой относительных частот называют ступенчатую функцию, состоящую из прямоугольников, основаниями которых служат частичные интервалы длины , а высоты равны отношению (плотность относительной частоты), где - относительная частота, соответствующая -му наблюденному значению. Площадь частичного -го прямоугольника равна -относительной частоте наблюдавшихся значений, попавших в -й интервал. Площадь гистограммы относительных частот равна единице.

Примеры с решениями

Пример 1. Выборка задана в виде распределения частот:

Найти распределение относительных частот.

Решение. Найдем объем выборки: Найдем относительные частоты:

Напишем распределение относительных частот:

Проверка:

Пример 2. Найти эмпирическую функцию распределения по заданному распределению выборки:

Решение. Найдем объем выборки: Наименьшее наблюденное значение равно единице, следовательно, при

Значение а именно наблюдалось 10 раз, поэтому при Значения а именно: наблюдались раз, следовательно, при Так как - наибольшее наблюденное значение, то при

Таким образом, искомая эмпирическая функция распределения имеет вид

График функции изображен на рисунке 1.

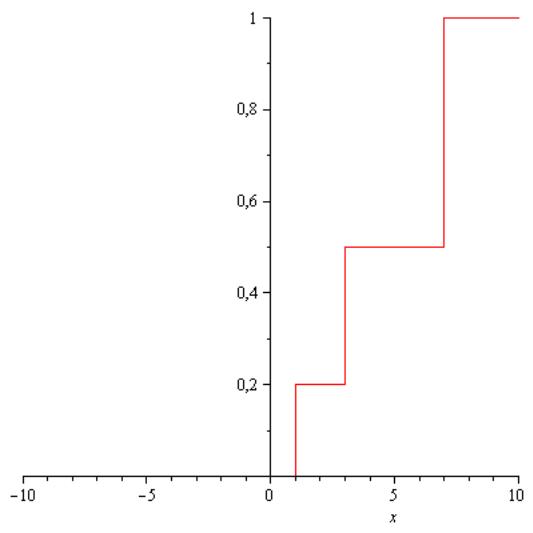
Рис.1

Пример 3. Построить гистограмму частот по данному распределению выборки объема :

Номер интервала	Частичный интервал	Сумма частот наблюдавшихся значений интервала	Плотность частоты
1	1-5	10	2.5
2	5-9	20	5
3	9-13	50	12.5
4	13-17	12	3
5	17-21	8	2

Решение. Построим на оси абсцисс заданные интервалы длины . Проведем над этими интервалами отрезки, параллельные оси абсцисс и находящиеся от нее на расстояниях, равных соответствующим плотностям частоты . Например, над интервалом построим отрезок, параллельный оси абсцисс, на расстоянии ; аналогично строят остальные отрезки. Гистограмма частот изображена на рисунке 2.

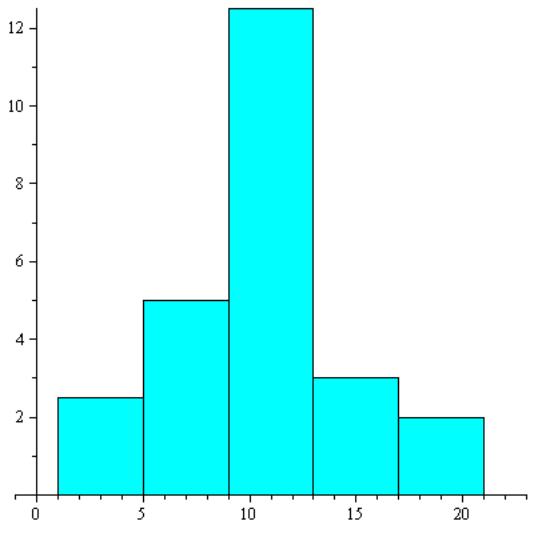
Рис. 2

Задачи

Задача 1. Выборка задана в виде распределения частот:

Найти распределение относительных частот.

Задача 2. Построить гистограмму частот по данному распределению выборки:

Номер интервала	Частичный интервал	Сумма частот наблюдавшихся значений интервала	Плотность частоты
1	2-7	7
2	7-12	10
3	12-17	20
4	17-22	12
5	22-27	4

Задача 3. Построить гистограмму относительных частот по данному распределению выборки:

Номер интервала	Частичный интервал	Сумма частот наблюдавшихся значений частичного интервала
1	2-5	6
2	5-8	10
3	8-11	4
4	11-14	5