4. Расчет зубчатых передач редукторов

1. Выполнить проектный расчет редукторной пары.

2. Выполнить проверочный расчет редукторной пары.

Расчет зубчатой закрытой передачи производится в два этапа: первый расчет – проектный, второй – проверочный. Проектный выполняется по допускаемым контактным напряжениям с целью определения геометрических параметров редукторной пары. В процессе проектного расчета задаются целым рядом табличных величин и коэффициентов; результаты некоторых расчетных величин округляют до целых или стандартных значений; в поиске оптимальных решений приходится неоднократно делать перерасчеты. Поэтому после окончательного определения параметров зацепления выполняют проверочный расчет.

4.1 Проектный расчет.

1. Определяем главный параметр – межосевое расстояние а_w, мм:

где К_а – вспомогательный коэффициент и для косозубых передач К_а=43,

-- коэффициент ширины венца колеса, равный 0,28…0,36 – для шестерни, расположенной симметрично относительно опор в проектируемых нестандартных одноступенчатых цилиндрических редукторах. Возьмем 0,32.

U =3,15 передаточное число редуктора.

Т₂ – вращающий момент на тихоходном валу редуктора, Н*м.

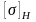= 514,3*10⁶ допускаемое контактное напряжение колеса с менее прочным зубом или среднее контактное напряжение, Н/мм².

- коэффициент неравномерности нагрузки по длине зуба. Для прирабатывающихся зубьев =1.

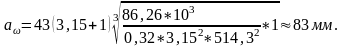
2. Определяем модуль зацепления m, мм:

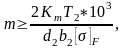
где К_m = 5,8 для косозубых передач, вспомогательный коэффициент.

d₂= делительный диаметр колеса.

b₂= ширина венца колеса.

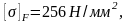
допускаемое напряжение изгиба материала колеса с менее прочным зубом.

берем по первому ряду 1,5.

3. Определяем угол наклона зубьев 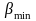для косозубых передач:

4. Определяем суммарное число зубьев шестерни и колеса: для косозубых колес

округляем до целого значения.

5. Уточняем действительную величину угла наклона зубьев для косозубых передач:

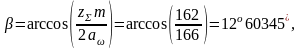
6. Определяем число зубьев шестерни:

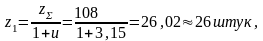
7. Определяем число зубьев колеса:

8. Определяем фактическое передаточное число u_ф и проверяем его отклонение от заданного u:

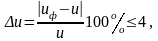
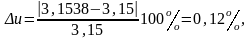
10. Определяем фактическое межосевое расстояние:

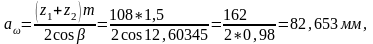
11. Определяем основные геометрические параметры передачи, мм.

Определяем делительный диаметр шестерни:

определяем делительный диаметр колеса:

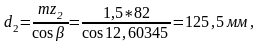
определяем диаметр вершин зубьев шестерни:

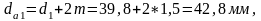
определяем диаметр вершин зубьев колеса:

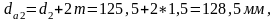
определяем диаметр впадин шестерни:

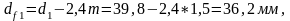
определяем диаметр впадин колеса:

определяем ширину венца колеса:

округляем до 28 мм,

определяем ширину венца шестерни:

Проверочный расчет

12. Проверяем межосевое расстояние:

13. Проверяем пригодность заготовок колес. Условие пригодности колес:

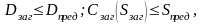
Диаметр заготовки шестерни :

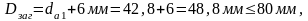
Размер колеса закрытой передачи :

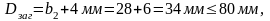
15. Проверяем контактные напряжения

где К- вспомогательный коэффициент. Для косозубых передач К = 376,

окружная сила в зацеплении.

- коэффициент, учитывающий распределение нагрузки между зубьями. Для косозубых определяется по графику в зависимости от окружной скорости колес

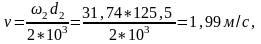и степени точности передачи.

=1,121.

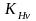- коэффициент динамической нагрузки, зависящий от окружной скорости колес и степени точности передачи и равен 1,03.

-коэффициент неравномерности нагрузки по длине зуба = 1. 514,9

Допускаемая недогрузка передачи не более 10% и перегрузка до 5%.

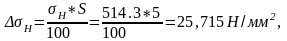
В нашем случае перегруз получился 0,194%, что в пределах допуска.

16. Проверяем напряжения изгиба зубьев шестерни 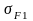и колеса , Н/мм²:

где m – модуль зацепления, мм; b₂ – ширина зубчатого венца колеса, мм; F_t – окружная сила в зацеплении, Н.

К_F зависит от степени точности передачи, определяемой по таблице. В нашем случае для 9-ой степени точности К_F =1.

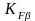- коэффициент неравномерности нагрузки по длине зуба. Для прирабатывающихся зубьев колес =1.

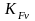- коэффициент динамической нагрузки, зависящий от окружной скорости колес и степени точности передачи. В нашем случае =1,07.

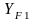и -коэффициент формы зуба шестерни и колеса. Определяется по таблице в зависимости от эквивалентного числа зубьев шестерни :

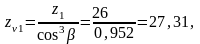=3,845.

и колеса:

=3,605.

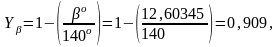
отклонение составляет:

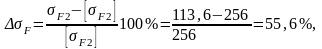
Параметры зубчатой цилиндрической передачи, мм

Проектный расчет
Параметр		Значение	Параметр	Значение
Межосевое расстояние аw		83	Угол наклона зубьев	12,60345о
Модуль зацепления m		1,5	Диаметр делительной окружности: Шестерни d1 Колеса d2	39,8 125,5
Ширина зубчатого венца: Шестерни b1 Колеса b2		31 28
Число зубьев: Шестерни z1 Колеса z2		26 82	Диаметр окружности вершин: Шестерни da1 Колеса da2	42,8 128,5
Вид зубьев			Диаметр окружности впадин: Шестерни df1 Колеса df2	36,2 121,9
Проверочный расчет
Параметр		Допускаемые значение	Расчетные значения	Примечание
Контактные напряжения Н/мм2		514,3	515	0,194
Напряжения изгиба, Н/мм2		Не считаем
		256	113,6	55,6