30.Дайте определение плотности распределения системы двух случайных величин.
Плотность
распределения системы представляет
собой предел отношения вероятности
попадания в малый прямоугольник к
площади этого прямоугольника, когда
оба его размера стремятся к нулю; она
может быть выражена как вторая смешанная
частная производная функции распределения
системы по обоим аргументам. Функция f
(х,у) называется плотностью распределения
системы.Предположим,
что функция F
(х, у) не
только непрерывна, но и дифференцируема;
тогда правая часть формулы (1) представляет
собой вторую смешанную частную производную
функции F
(х,у) по х
и у. Обозначим эту производную f
(х,у):
31.Свойства плотности распределения системы двух случайных величин
1. Плотность распределения системы есть функция неотрицательная:
f (х, у) ≥ 0.
Это ясно из того, что плотность распределения есть предел отношения двух неотрицательных величин: вероятности попадания в прямоугольник и площади прямоугольника — и, следовательно, отрицательной быть не может.
2.
Двойной интеграл в бесконечных пределах
от плотности распределения системы
равен единице:
Геометрически
это свойство означает, что полный объем
тела, ограниченного поверхностью
распределения и плоскостью хОу,
равен единице.
32.Дайте определение и укажите основные свойства прв системы величин.
Разделим
вероятность попадания в прямоугольник
RΔ
на площадь этого прямоугольника и
перейдем к пределу при Δх
→ 0 и Δу
→ 0:
Предположим, что функция F (х, у) не только непрерывна, но и дифференцируема; тогда правая часть формулы (1) представляет собой вторую смешанную частную производную функции F (х,у) по х и у. Обозначим эту производную f (х,у): плотность распределения системы представляет собой предел отношения вероятности попадания в малый прямоугольник к площади этого прямоугольника, когда оба его размера стремятся к нулю; она может быть выражена как вторая смешанная частная производная функции распределения системы по обоим аргументам. Если воспользоваться «механической» интерпретацией распределения системы как распределения единичной массы по плоскости хОу, функция f (х, у) представляет собой плотность распределения массы в точке (х, у).
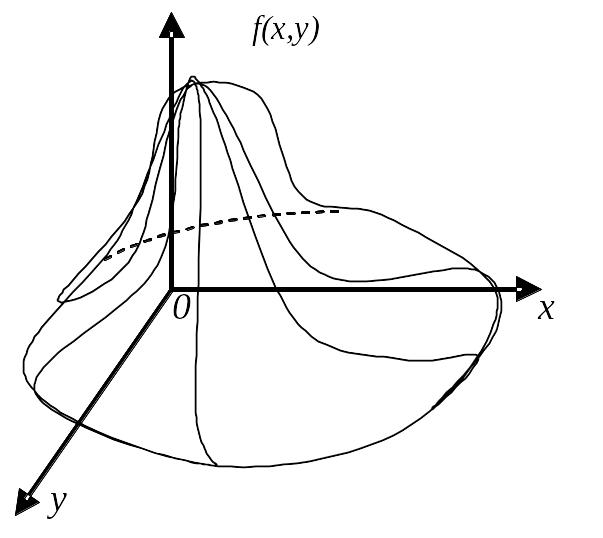
Геометрически функцию
f(х,у) можно изобразить некоторой поверхностью.
Эта поверхность аналогична кривой распределения для одной случайной величины и называется поверхностью распределения.
Очевидно,
элемент вероятности есть не что иное,
как вероятность попадания в элементарный
прямоугольник со сторонами dх, dy,
примыкающий к точке (x, у).
Пользуясь
понятием элемента вероятности, выведем
выражение для вероятности попадания
случайной точки в произвольную область
D.
Эта
вероятность, очевидно, может быть
получена суммированием (интегрированием)
элементов вероятности по всей области
D:
1. Плотность распределения системы есть функция неотрицательная:
f (х, у) ≥ 0.
Это ясно из того, что плотность распределения есть предел отношения двух неотрицательных величин: вероятности попадания в прямоугольник и площади прямоугольника — и, следовательно, отрицательной быть не может.
2. Двойной интеграл в бесконечных пределах от плотности распределения системы равен единице: Геометрически это свойство означает, что полный объем тела, ограниченного поверхностью распределения и плоскостью хОу, равен единице.