5 Пропорції
Пропорціями називається розмірне відношення двох елементів форми. Закономірні відношення діляться на дві групи: простих відношень, що будуються на простих раціональних числах, та ірраціональних – похідних від геометричних побудов.
В простих відношеннях числова залежність двох величин виражена дробовим числом, де чисельник і знаменник представлені цілими числами зазвичай в межах від 1 до 6.
На відношенні 1:1 будуються найпростіші геометричні форми – квадрат, куб. Відношення 1:2, 1:3, 1:4, 1:5, 1:6 в прямокутній формі дають повторення квадрату ціле число разів. Відношення 2:3, 2:5, 3:4, 3:5, 5:6 містить в собі модуль, що вкладається в ціле число разів в кожній геометричній величині, що входить в співвідношення.

Просте співвідношення
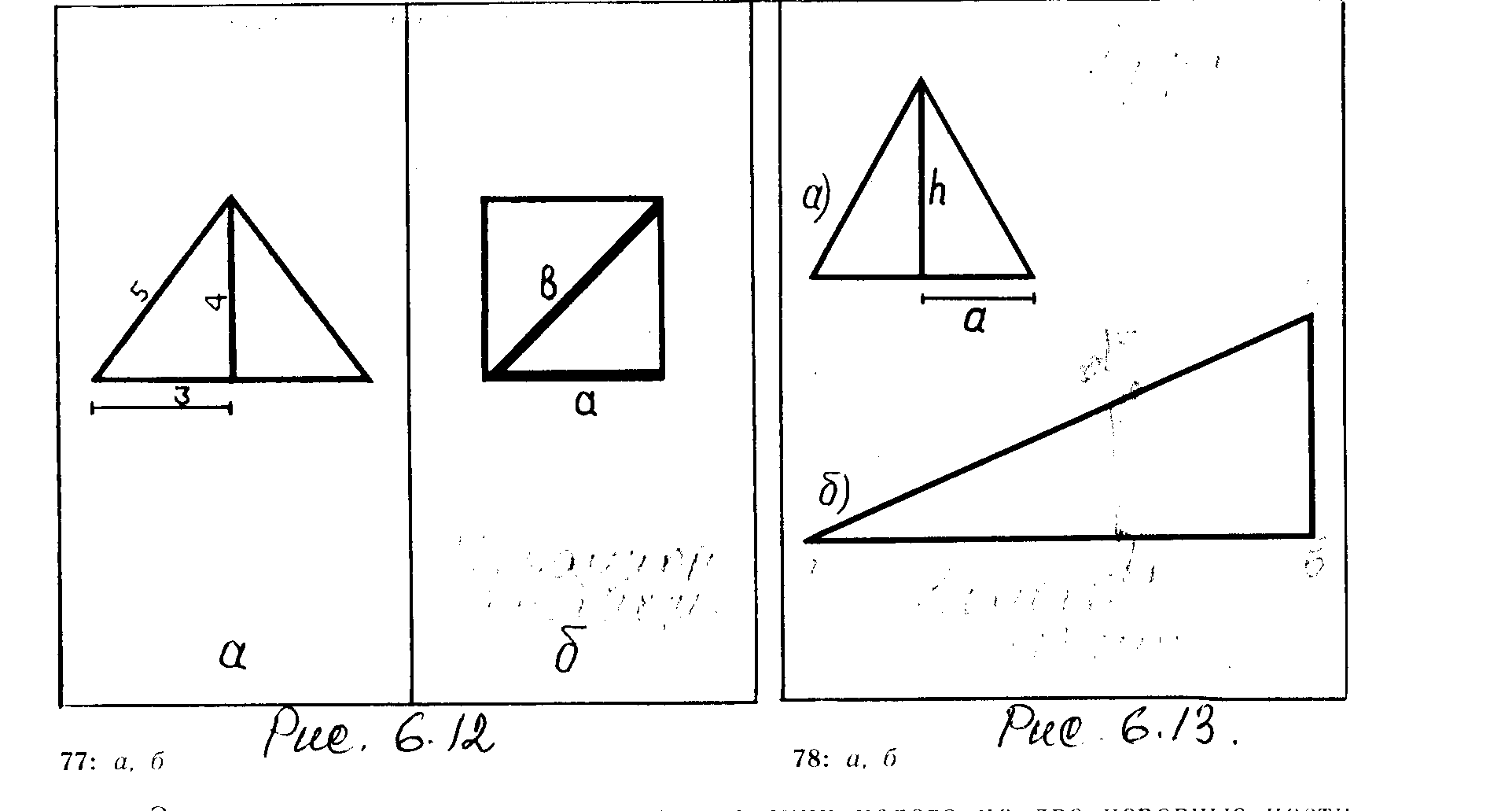
Прикладом простого співвідношення є єгипетський трикутник. В ньому виділяються наступні співвідношення:
Відношення діагоналі до його сторони

Відношення висоти рівностороннього трикутника до половини його основи

Так званий «золотий переріз», що виражається дробовим числом 1:1,62…
|
|
|
а) |
б) |
Єгипетський трикутник |
«Золотий переріз» отримують при діленні цілого на дві нерівні частини таким чином, щоб ціле відносилось до більшої частини, як більша частина до меншої, тобто:

«Золотий переріз» став відомим ще в давні часи. Сам термін в науку ввів Леонардо да Вінчі. «Золотий переріз» отримують при побудові п’ятикінечної зірки, вписаної в правильний п’ятикутник, де в кожній точці перетину сторони зірки діляться на дві частини відповідно «золотого перерізу»
На практиці часто застосовують наближений «золотий переріз»: 3:5, 5:8, 8:13, 13:21 і т.д. Тут кожен наступний член ряду дорівнює сумі двох попередніх. Цей ряд називається рядом Фібоначчі, а члени ряду – числами Фібоначчі.
До ірраціональних належать відношення, що випливають з геометрії «динамічних» прямокутників.
В пластичному мистецтві пропорціями визначається співрозмірність та гармонійність елементів форми, різних співвідношень по ширині, глибині, висоті всіх частин форми один з одним та з цілим.
Більш складним видом пропорційних співвідношень є подібність двох чи більше частин форми за розмірним відношенням елементів кожної з них.
Метод подібності в дизайні та архітектурі відноситься переважно до вертикальних та горизонтальних поділів, що в більшості випадків дозволяє розглядати форму як систему прямокутників. Ознаками їх подібності є паралельність або перпендикулярність сторін та діагоналей.
На цьому ґрунтується геометричний метод побудови пропорцій. Використовуючи його, можна приводити до єдиного відношення всі частини форми. Розрізняють два типи побудови: співпорядкований та розподільний.
Співпорядкування: менший елемент береться похідним від заданого більшого, будується на його геометричній подібності. Розподілення: менший прямокутник є не лише похідним більшого, але й його частиною, розділюючи останній.
Співпорядкування та розподіл служать основними прийомами побудови цілого та частин.
Вибір пропорцій визначається, перш за все, матеріалом, функціональним призначенням виробу, умовами його застосування, а також врахуванням технологічних та ергономічних вимог.