
- •Розділ 1. Математичні основи синтезу логічних схем
- •1.1. Деякі поняття і визначення булевої алгебри
- •1.2. Способи задання булевих функцій
- •1.3. Булеві функції від однієї і двох змінних
- •1.4. Принцип суперпозиції логічних функцій. Пріоритет операцій
- •1.5. Аксіоми та закони булевої алгебри
- •Аксіоми кон’юнкції, диз’юнкції і заперечення:
- •1.7. Аксіоми та закони алгебри Жегалкіна
- •1. Комутативний закон
- •2. Сполучний закон
- •3. Розподільний закон по відношенню до додавання за модулем 2
- •1.8. Аксіоми та закони для функцій Шеффера та Пірса
- •1.9. Аналітичне подання булевих функцій
- •1.10. Класи булевих функцій. Теорема про повноту
- •1.11. Розвинення логічних функцій за змінними
- •1.12. Зв’язок між дднф і дкнф. Канонічні нормальні форми
1.3. Булеві функції від однієї і двох змінних
Будь-яку логічну функцію, яка залежить від n змінних (n>2), можна виразити через функції від однієї або двох змінних. Тому логічні функції, що залежать від нуля, однієї і двох змінних, посідають особливе місце в теорії логічних функцій. Ці функції називають елементарними функціями.
Розглянемо ці функції.
При
![]() є дві різні функції:
є дві різні функції:
![]() і
і
![]() .
Функцію
називають константою 0, а функцію
– константою 1.
.
Функцію
називають константою 0, а функцію
– константою 1.
При
![]() є чотири
є чотири
![]() ,
які наведено в табл. 7.
Ці функції описують роботу одновходових
цифрових схем.
,
які наведено в табл. 7.
Ці функції описують роботу одновходових
цифрових схем.
Таблиця 7
-
x
0
1
Функція
Назва функції
0
0
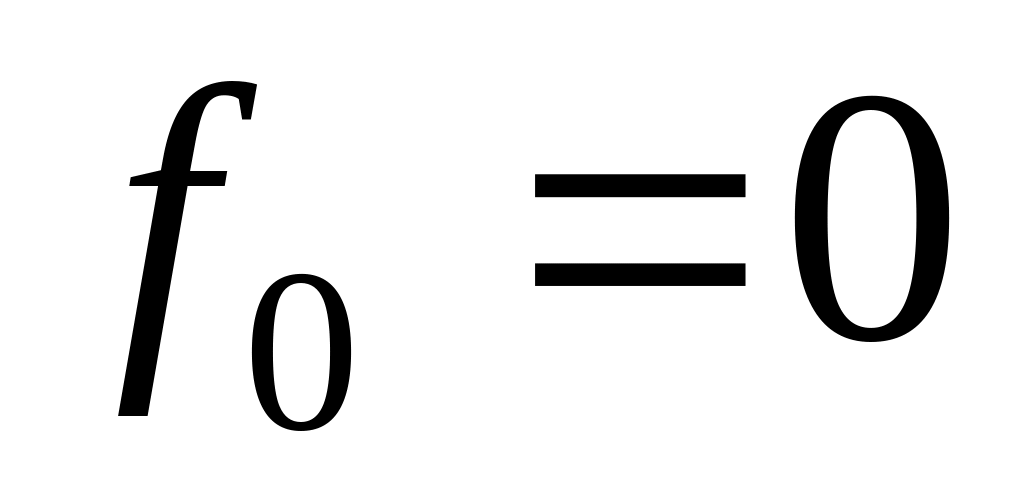
Константа 0
0
1
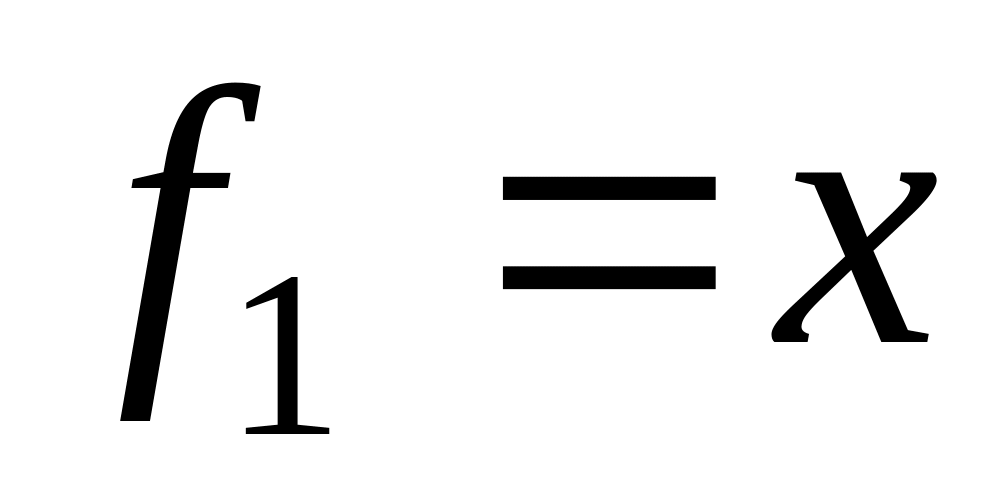
Еквівалентність
1
0
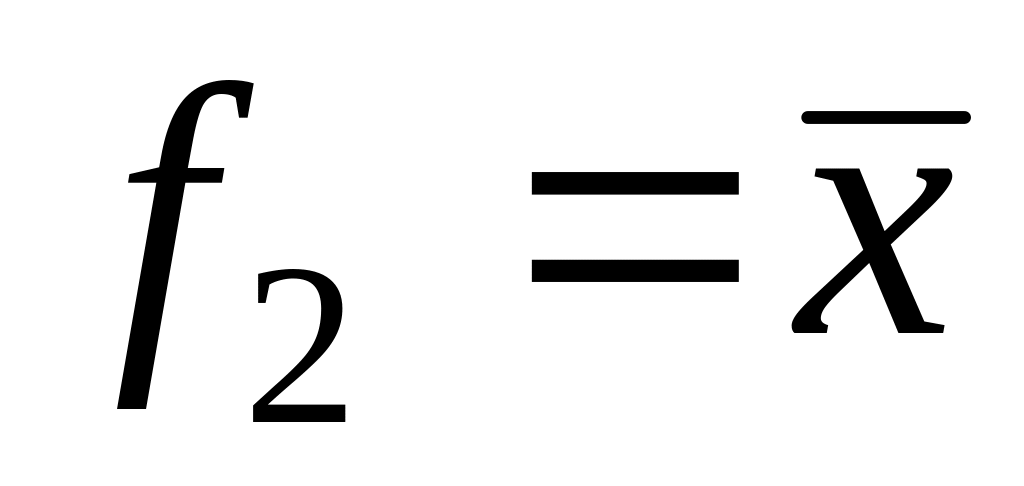
Інверсія x
1
1
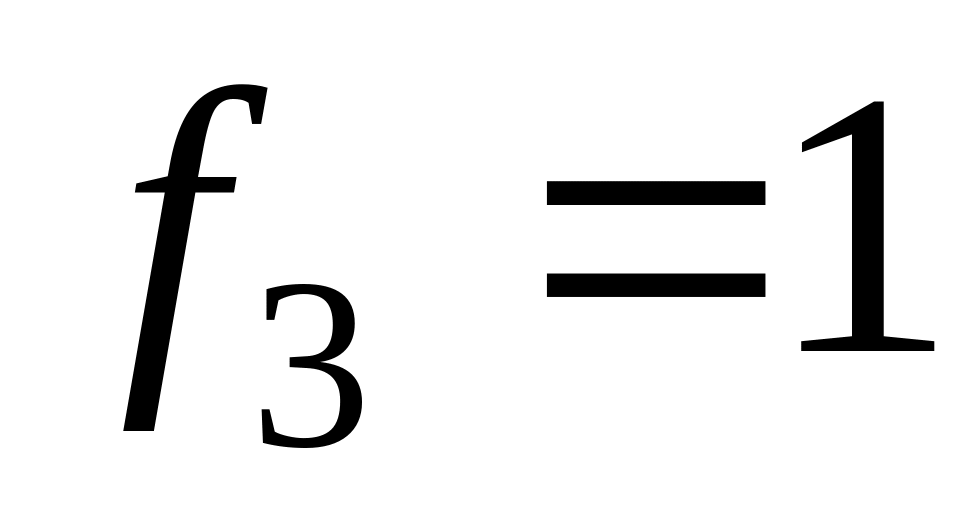
Константа 1
Булеві
функції
![]() і
і
![]() є константами 0 і 1; вони приймають
відповідно значення 0 і 1 при всіх
значеннях аргументу, тобто збігаються
з функціями нуля змінних. Ці функції
описують схеми, виходи яких постійно
під’єднані до рівнів логічного нуля і
логічної одиниці відповідно. Значення
функції
є константами 0 і 1; вони приймають
відповідно значення 0 і 1 при всіх
значеннях аргументу, тобто збігаються
з функціями нуля змінних. Ці функції
описують схеми, виходи яких постійно
під’єднані до рівнів логічного нуля і
логічної одиниці відповідно. Значення
функції
![]() співпадає зі значенням аргументу x.
Логічний пристрій, який реалізує
,
називають повторювачем і в схемах
позначають так, як показано на рис. 2,а.
Булева функція
співпадає зі значенням аргументу x.
Логічний пристрій, який реалізує
,
називають повторювачем і в схемах
позначають так, як показано на рис. 2,а.
Булева функція
![]() перетворює 0 в 1, а 1 в 0. Таке перетворення
називають інвертуванням.
Логічний пристрій, який реалізовує цю
функцію, називають інвертором
або логічним елементом “НЕ”
(рис. 2.б)
перетворює 0 в 1, а 1 в 0. Таке перетворення
називають інвертуванням.
Логічний пристрій, який реалізовує цю
функцію, називають інвертором
або логічним елементом “НЕ”
(рис. 2.б)
Європейська система позначень

 а)
б)
а)
б)
x
1
![]() x
1
x
1
![]()
Американська система позначень

![]()
x
x![]()
Рис. 2
Булеві
функції від двох змінних (їх всього
![]() )
подано в табл. 8.
)
подано в табл. 8.
Усі булеві функції від двох змінних можна розбити на п’ять груп:
В
групу I входять функції
і
![]() ,
які зберігають постійні значення 0 і
1, відповідно, тобто, вони є константами.
,
які зберігають постійні значення 0 і
1, відповідно, тобто, вони є константами.
В
групу II входять чотири функції
![]() ,
,
![]() ,
,
![]() і
і
![]() ,
які істотно залежать тільки від одного
аргументу. Це вироджені функції. Решта
(десять) функцій залежать від двох
змінних.
,
які істотно залежать тільки від одного
аргументу. Це вироджені функції. Решта
(десять) функцій залежать від двох
змінних.
В
групу III входять чотири функції, які
приймають значення 1 тільки на одному
наборі:
![]() (набір 11),
(набір 11),
![]() (набір 10),
(набір 10),
![]() (набір
01) і
(набір
01) і
![]() (набір 00).
(набір 00).
В групу
IV входять чотири функції (двоїсті до
функцій третьої групи), які на трьох
наборах приймають значення 1 і тільки
на одному наборі —
значення 0, а саме:
![]() (набір 00),
(набір 00),
![]() (набір 01),
(набір 01),
![]() (набір 10) і
(набір 10) і
![]() (набір 11).
(набір 11).
В
групу V входять дві функції,
які істотно залежать від
кожного із аргументів
і приймають на двох наборах
значення 0, а на двох —
значення 1:
![]() ,
яка на наборах 01 і 10
приймає значення 1, а на наборах
11 і 00 приймає значення 1;
,
яка на наборах 01 і 10
приймає значення 1, а на наборах
11 і 00 приймає значення 1;
![]() ,
яка на наборах 00 і 11
приймає значення 1, а на наборах
01 і 10 приймає значення 0.
,
яка на наборах 00 і 11
приймає значення 1, а на наборах
01 і 10 приймає значення 0.
Таблиця 6 |
||||||
|
0 |
0 |
1 |
1 |
Функція |
Назва функції |
|
0 |
1 |
0 |
1 |
|
|
I |
0 |
0 |
0 |
0 |
|
Константа 0 |
III |
0 |
0 |
0 |
1 |
|
Кон’юнкція |
III |
0 |
0 |
1 |
0 |
|
Заборона
по
|
II |
0 |
0 |
1 |
1 |
|
Тотожно
|
III |
0 |
1 |
0 |
0 |
|
Заборона по |
II |
0 |
1 |
0 |
1 |
|
Тотожно |
V |
0 |
1 |
1 |
0 |
|
Сума по модулю 2 |
IV |
0 |
1 |
1 |
1 |
|
Диз’юнкція |
III |
1 |
0 |
0 |
0 |
|
Стрілка Пірса |
V |
1 |
0 |
0 |
1 |
|
Еквівалентність |
II |
1 |
0 |
1 |
0 |
|
Інверсія |
IV |
1 |
0 |
1 |
1 |
|
Імплікація
|
II |
1 |
1 |
0 |
0 |
|
Інверсія |
IV |
1 |
1 |
0 |
1 |
|
Імплікація
|
IV |
1 |
1 |
1 |
0 |
|
Штрих Шеффера |
I |
1 |
1 |
1 |
1 |
|
Константа 1 |
З наведених 16-ти логічних функцій на практиці використовуються шість:
1. (функція “ I ”),
2.
![]() (функція “АБО”),
(функція “АБО”),
3.
![]() (сума
за модулем 2),
(сума
за модулем 2),
4.
![]() (еквівалентність
або
заперечення
суми за модулем 2),
(еквівалентність
або
заперечення
суми за модулем 2),
5.
![]() (функція Пірса
або “ АБО
– НЕ”),
(функція Пірса
або “ АБО
– НЕ”),
6.
![]() (функція Шеффера
або “
І – НЕ”.
(функція Шеффера
або “
І – НЕ”.
Логічні елементи, які реалізовують дані функції, мають аналогічні назви, а їх позначення наведено на рис. 3,а-е.
Європейська система позначень
а) б) в)

![]()
![]() &
&
![]() 1
1
![]() =1
=1
![]()
г) д) е)

&
![]()
![]()
![]() =1
=1
![]()
Американська система позначень

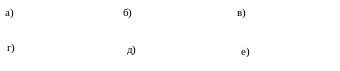

Рис. 3
