Решение
В модели Леонтьева валовой выпуск X,
конечный продукт Y и
промежуточное потребление
связаны системой уравнений:
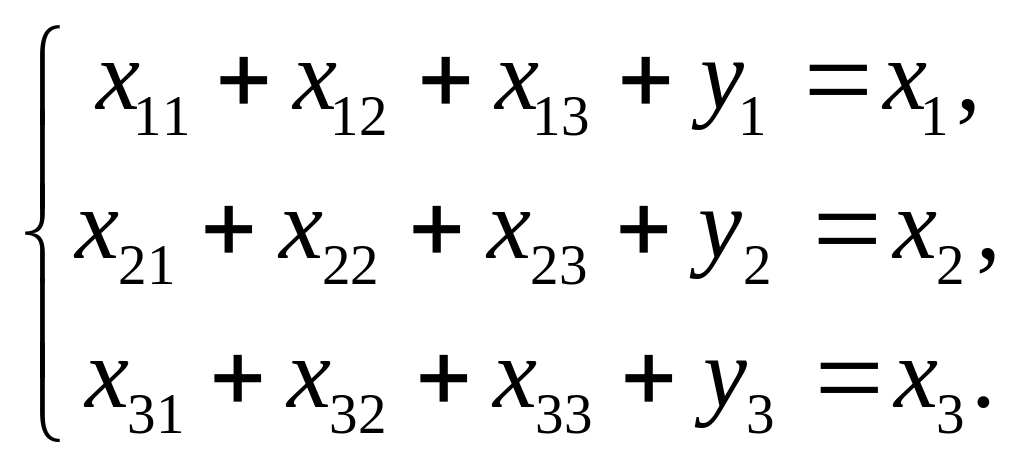
Тогда объемы промежуточной продукции можно представить матрицей:
.
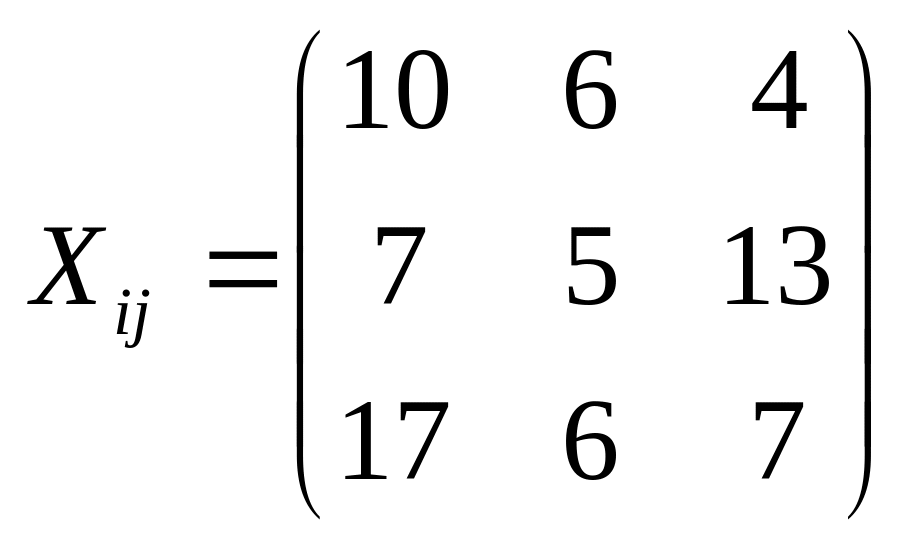2.6. Статическая модель Леонтьева многоотраслевой экономики продуктивна. Тогда матрица коэффициентов прямых затрат может иметь вид…
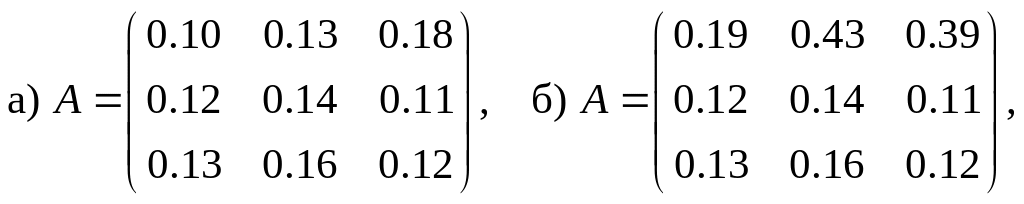
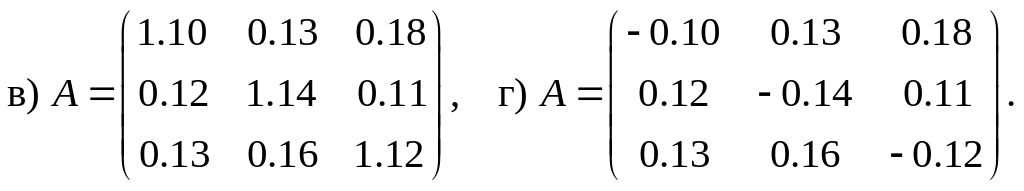
Решение
Во-первых, коэффициенты прямых затрат
вычисляются по формуле
,
где
—
объем промежуточной продукции
-ой
отрасли, который используется в
-ой
отрасли,
—
объем валового выпуска в
-ой
отрасли, то есть
.
Во-вторых, модель Леонтьева продуктивна,
если сумма элементов каждой строки
матрицы не больше единицы и хотя бы для
одной строки эта сумма меньше единицы.
Обоим этим условиям удовлетворяет
матрица
.
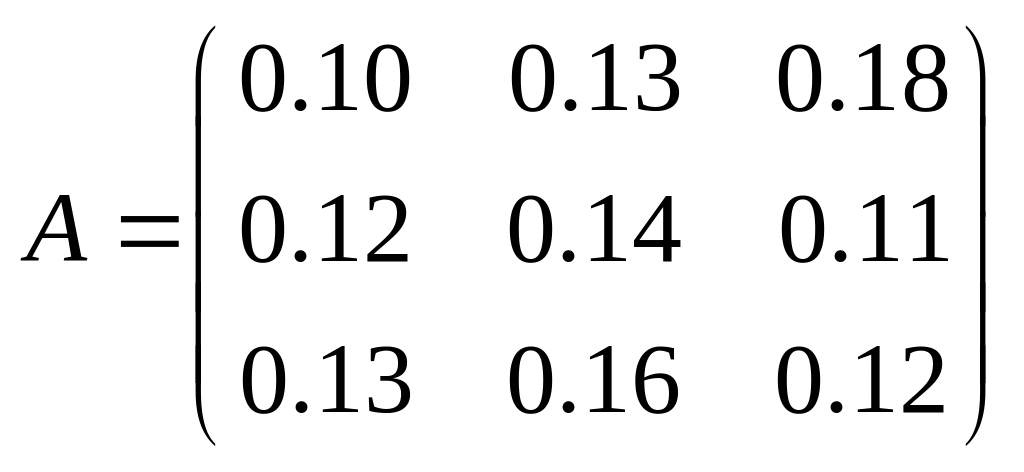2.7. В линейной статической модели
Леонтьева объемы конечного продукта
представлены вектором
,
матрица коэффициентов полных затрат
имеет вид
.
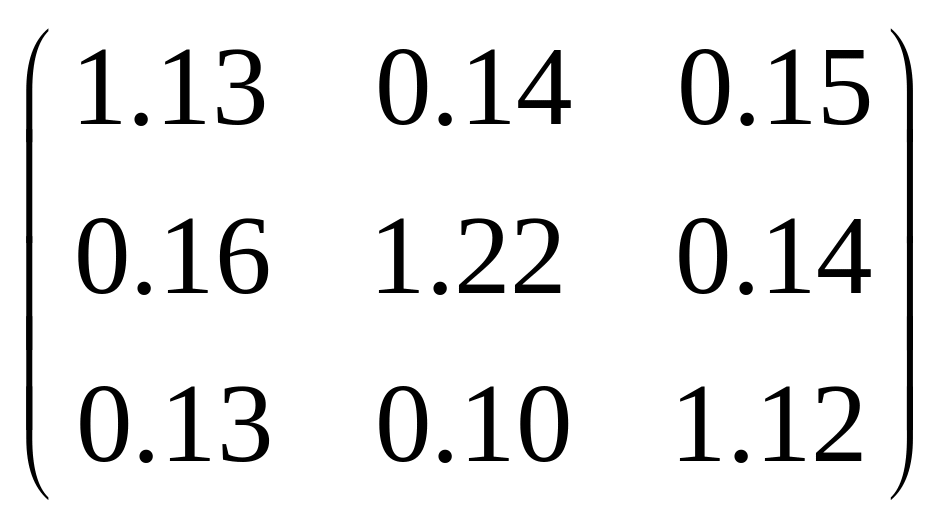Тогда объемы валовых выпусков будут
представлены вектором…
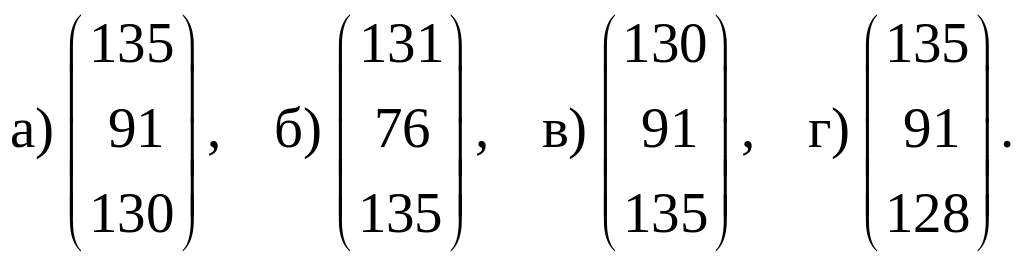
Решение
Объемы валовых выпусков (вектор X)
определяются в модели межотраслевого
баланса из уравнения
,
где B — матрица
коэффициентов полных затрат, а Y —
вектор конечного продукта. Тогда
.
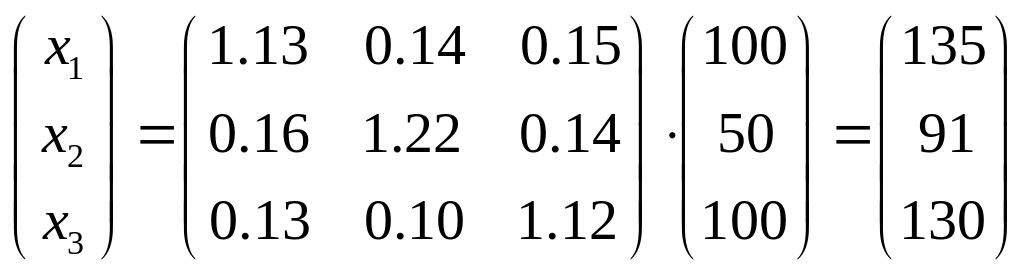2.8. Матрица коэффициентов прямых
затрат линейной статической модели
Леонтьева имеет вид
,
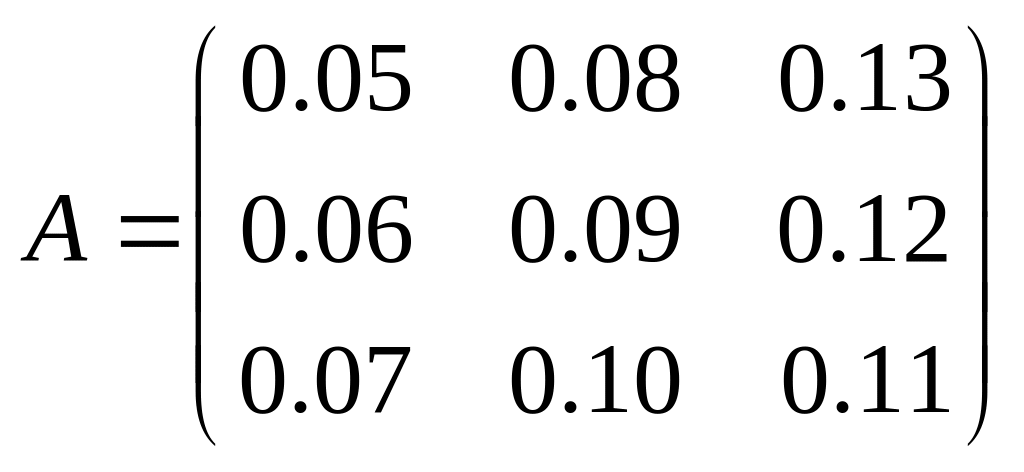а объемы валовых выпусков представлены
вектором
.
Тогда объемы конечного продукта будут
представлены вектором…
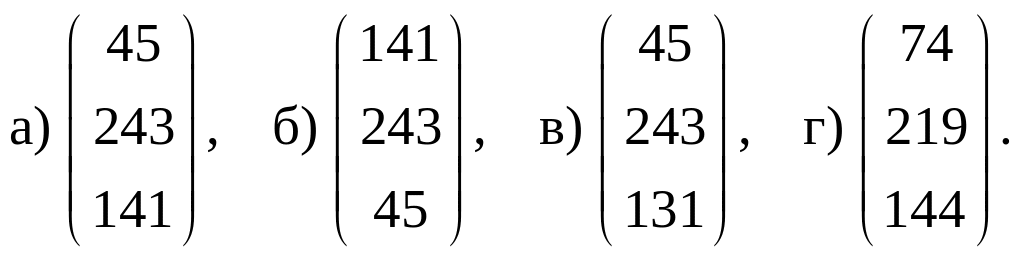
Решение
Статическая линейная модель Леонтьева
в матричной форме моделируется системой
,
где E — единичная
матрица. Следовательно, объемы конечного
продукта Y
определяются как
,
то есть
.
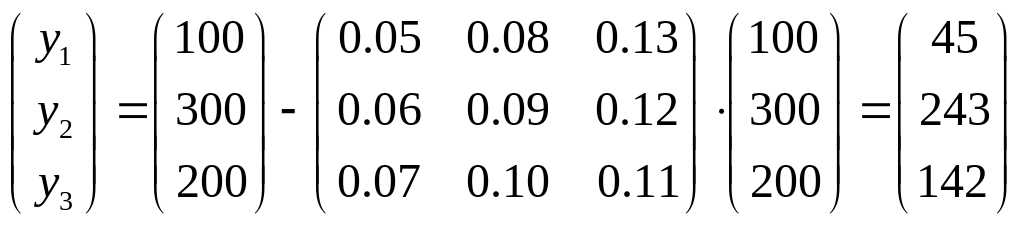2.9. Матрица коэффициентов полных затрат статической модели Леонтьева может иметь вид…
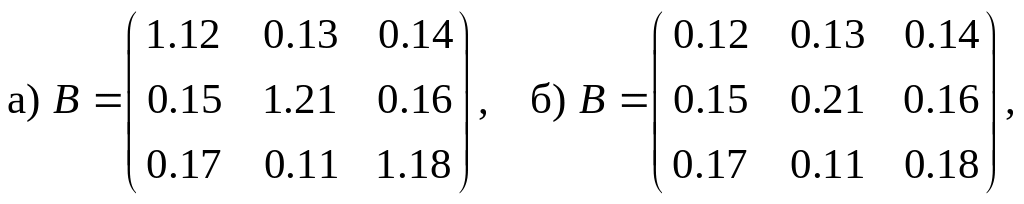
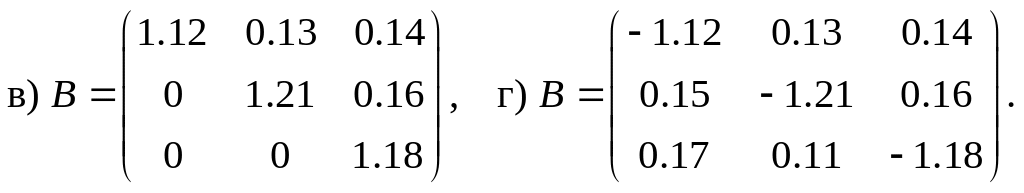
Решение
Коэффициенты полных затрат
показывают, на сколько единиц увеличится
валовой выпуск
-ой
отрасли при увеличении конечного выпуска
в
-ой
отрасли на одну единицу. Поэтому
,
а
,
при
.
Этим условиям удовлетворяет матрица
.
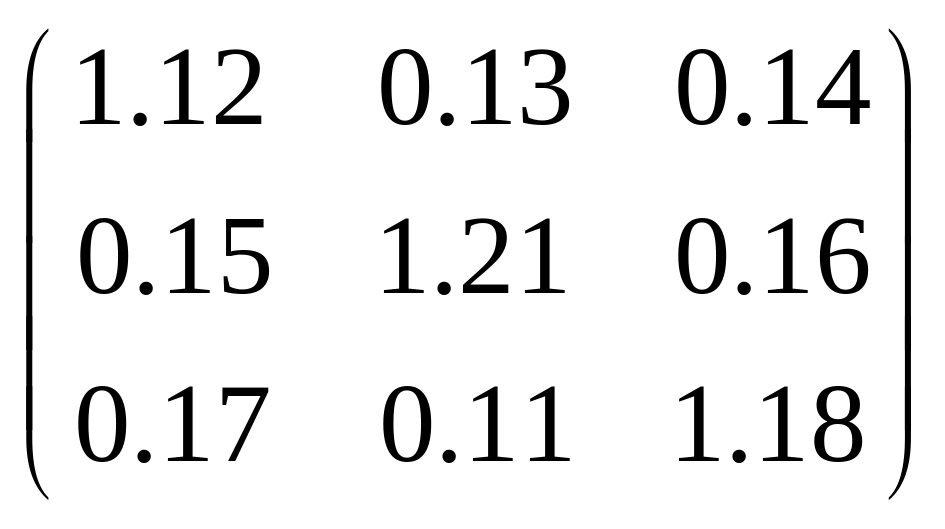2.10. Матрица коэффициентов прямых
затрат линейной статической модели
Леонтьева имеет вид
.
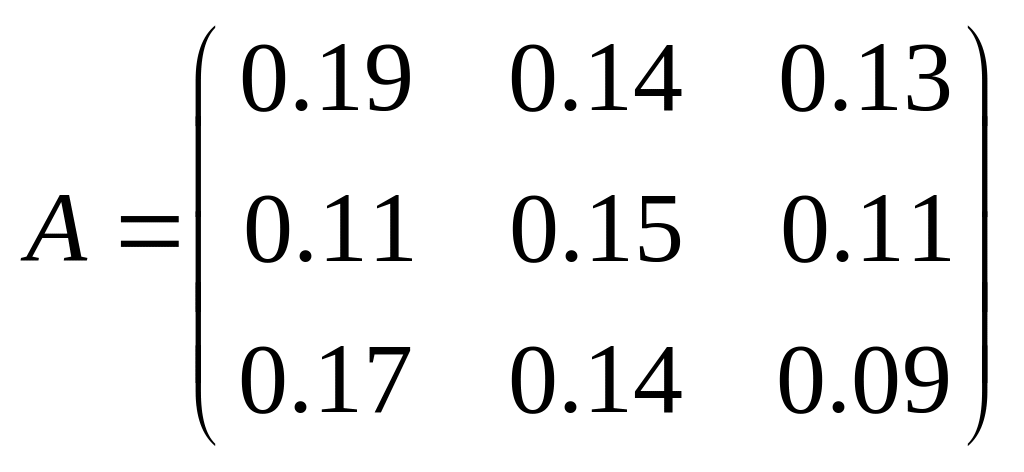Тогда модель межотраслевого баланса
представляется системой уравнений…
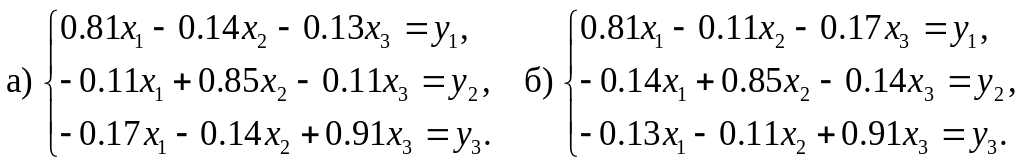
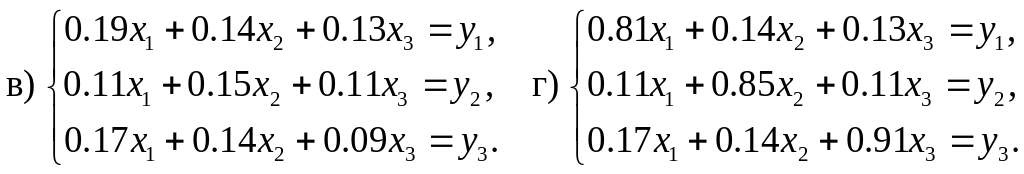
Решение
Статическая линейная модель Леонтьева в матричной форме моделируется системой , где E — единичная матрица. Следовательно, система линейных уравнений модели межотраслевого баланса имеет вид:
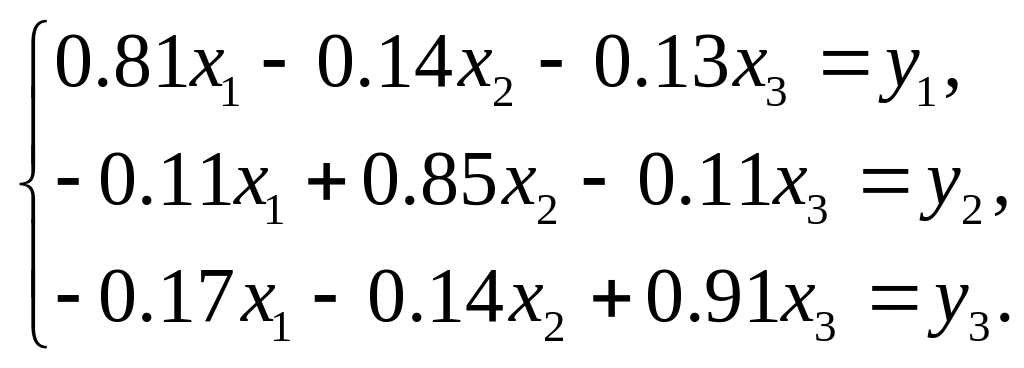
2.11. Статическая линейная модель межотраслевого баланса Леонтьева представлена системой уравнений:
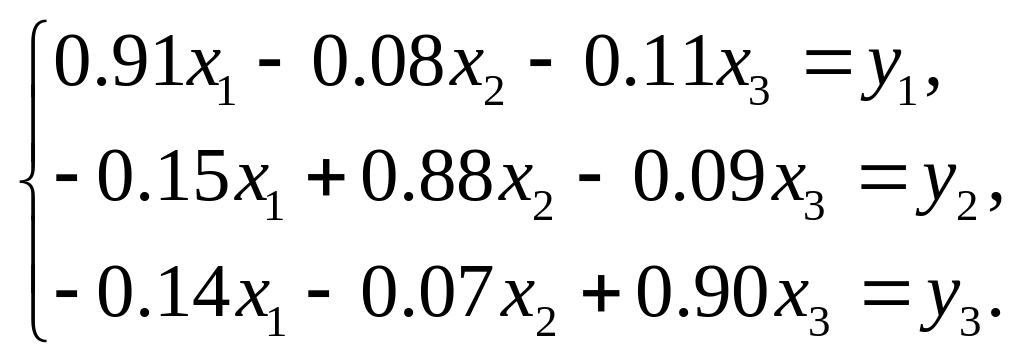
Тогда матрица коэффициентов прямых затрат равна…
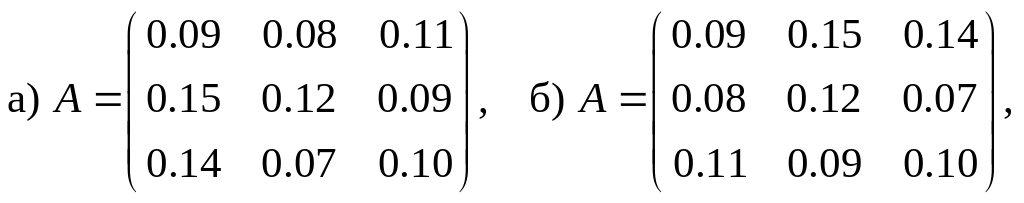
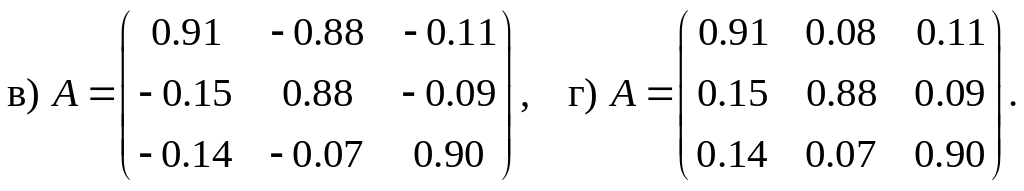
Решение
Статическая линейная модель Леонтьева в матричной форме моделируется системой , где E — единичная матрица. Следовательно, матрица коэффициентов прямых затрат имеет вид:
.
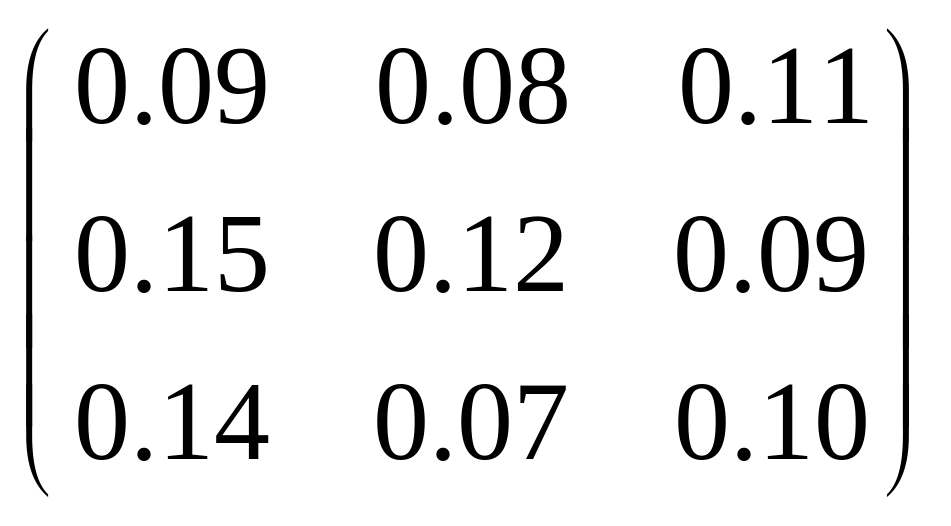3. Задачи к самостоятельной работе
Заданы матрица коэффициентов прямых
затрат трех отраслей
и вектор конечной продукции Y.
Требуется:
1. проверить продуктивность матрицы А;
2. построить баланс производства и распределения продукции отраслей.
(В табл. 2 указан номер задачи. В соответствии с ним из табл. 2 выберите числовые значения для табл. 3).
Таблица 2
№ |
Для первой строки |
Для второй строки |
Для третей строки |
|||||||||
1А |
2А |
3А |
4А |
1Б |
2Б |
3Б |
4Б |
1В |
2В |
3В |
4В |
|
1 |
0,1 |
0,2 |
0,1 |
200 |
0,2 |
0,1 |
0 |
150 |
0 |
0,2 |
0,1 |
250 |
2 |
0 |
0,1 |
0,2 |
180 |
0,1 |
0,2 |
0,1 |
200 |
0,2 |
0,1 |
0,2 |
200 |
3 |
0,2 |
0,1 |
0,2 |
150 |
0 |
0,1 |
0,2 |
180 |
0,1 |
0 |
0,1 |
100 |
4 |
0,1 |
0 |
0,1 |
100 |
0,1 |
0 |
0,2 |
300 |
0,2 |
0,1 |
0 |
160 |
5 |
0,2 |
0,3 |
0 |
120 |
0,3 |
0,1 |
0,2 |
250 |
0,1 |
0 |
0,3 |
180 |
6 |
0,3 |
0,4 |
0,1 |
200 |
0,1 |
0,2 |
0,4 |
300 |
0,3 |
0,4 |
0,1 |
200 |
7 |
0,1 |
0,2 |
0,4 |
100 |
0 |
0,4 |
0,1 |
200 |
0,1 |
0,3 |
0,4 |
100 |
8 |
0 |
0,4 |
0,1 |
160 |
0,4 |
0,1 |
0 |
180 |
0,3 |
0 |
0,1 |
150 |
9 |
0,4 |
0,2 |
0,3 |
180 |
0,2 |
0,1 |
0 |
200 |
0,2 |
0,1 |
0 |
160 |
10 |
0,1 |
0,1 |
0,2 |
160 |
0,1 |
0,2 |
0,3 |
180 |
0,2 |
0,2 |
0,3 |
170 |
Таблица 3
Отрасли |
Коэффициенты прямых затрат, |
Конечный продукт Y |
||
1 |
2 |
3 |
||
1 |
1А |
2А |
3А |
4А |
2 |
1Б |
2Б |
3Б |
4Б |
3 |
1В |
2В |
3В |
4В |