8. Определение монотонной функции. Теорема Вейерштрасса о существовании односторонних пределов у монотонной функции Монотонные функции
Функция называется возрастающей на отрезке [а, b], принадлежащем области определения функции, если любому большему значению аргумента из этого отрезка соответствует большее значение функции
x2 > x1→ f (x2) > f (x1) х1, x2 [a, b].
Функция называется убывающей на отрезке [a, b], если любому большему значению аргумента из этого интервала соответствуют меньшие значения функции
x2 > x1→ f (x2) < f (x1) х1, x2 [a, b].
Функции, убывающие или возрастающие на некотором числовом промежутке, называются монотонными функциями. Участки возрастания функции на рисунке отмечены синим цветом (в чёрно белом варианте более толстым форматом). Участки убывания отмечены красным цветом (в чёрно белом варианте более тонким форматом), рис. 5.3.
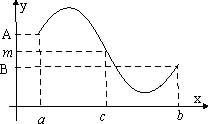
9. Теорема Больцано-Коши для непрерывной функции на отрезке
Пусть
функция f
(x)
определена и непрерывна на отрезке [a,
b].
Если на концах этого отрезка функция
принимает неравные значения f(a)
= A, f
(b)
= B, то, каково бы ни было число m
(A,
B), найдётся такая точка х
= с
(a,
b),
что f
(c)
= m
.
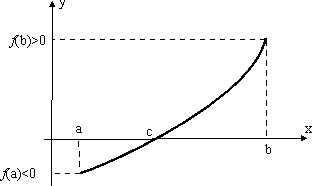
Как
частный случай имеет место следующее
утверждение. Пусть функция f(x)
непрерывна на отрезке [a,
b]
и на концах отрезка имеет значения
разных знаков. Тогда существует внутренняя
точка отрезка с
(a,
b),
в которой f(c)
= 0.
Данная теорема имеет простой
геометрический смысл: непрерывная
кривая при переходе из одной полуплоскости,
граница которой является ось абсцисс,
в другую, пересекает эту ось
Теорема.
Если функция f
(x) определена и непрерывна на отрезке
[a,
b]
, то она на этом отрезке принимает по
крайней мере один раз любое значение,
заключённое между её наименьшими и
наибольшими значениями.
Д о к
а з а т е л ь с т в о. Будем считать, что А
< m
< B. Рассмотрим на промежутке [а,
b]
вспомогательную функцию φ (x) = f
(x) − m.
Эта функция непрерывна на промежутке
[а,
b]
и на концах его имеет разные знаки: φ
(a)
= f
(a)
− m
= A − m
< 0 и φ(b)
= f(b)
− m
= B − m
> 0. Тогда, по второй теореме Больцано
– Коши, между a
и b
найдётся точка х
= с,
для которой φ(c)
= m.
Что и требовалось доказать.
10.Теорема Вейерштрасса об ограниченности непрерывной функции на отрезке.
Если функция f (x) определена и непрерывна в замкнутом промежутке [a, b], то она на этом промежутке ограничена. Доказательство. Функция f (х) ограничена на промежутке [а, b], если существуют такие конечные числа m и M, что m ≤ f (х) ≤ М при a ≤ x ≤ b. Допустим, что функция f (х) при изменении х в промежутке [а, b] оказывается неограниченной. В таком случае для каждого натурального числа n найдётся в промежутке [а, b] такое значение х = хn, что f ( xn) ≥ n. Однако по лемме Больцано – Вейерштрасса из этой ограниченной последовательности {xn} можно выделить сходящуюся частичную подпоследовательность:
Причем, очевидно, х0 [a, b]. Вследствие непрерывности функции в точке х0 должно быть выполнено
Однако, в силу f (xn) ≥ n имеем
Полученное противоречие и доказывает теорему.