Оптична властивість параболи

Теорема 1. Дотична до параболи утворює однакові кути з фокальним радіусом точки дотику і віссю параболи.

Д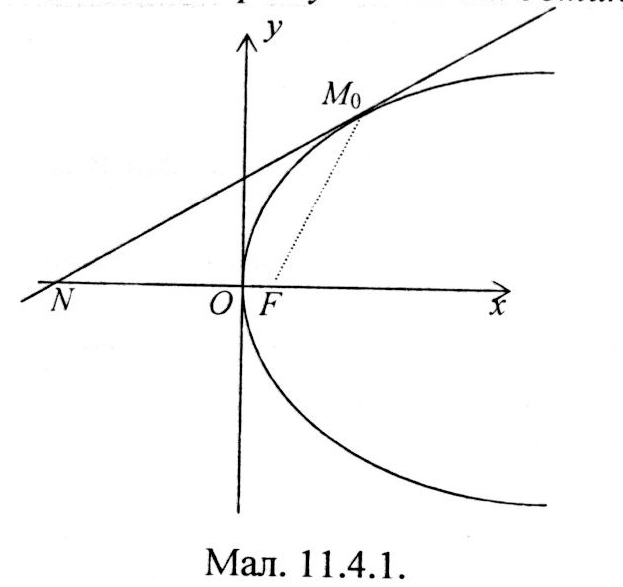 оведення. Нехай - задана парабола. Її дотична в точці задається рівнянням

Знайдемо координати точки перетину дотичної з віссю параболи (віссю ):

Отже,

Оскільки

і

То трикутник рівнобедрений. Отже, Що й вимагалось довести.

Задача 1. Фокус параболи співпадає з початком координат. Знайти

Розв’язання. Фокальна хорда даної параболи лежить на осі її кінці і . Оскільки то

Відповідь:

Задача 2. Довести, що дві софокусні параболи, які мають спільну вісь і спільний фокус, розміщений між їх вершинами, перетинаються під прямим кутом.

Розв’язання. Розглянемо софокусні параболи і фокус яких співпадає з початком координат. Знайдемо координати їх точок перетину:

Отже, параболи перетинаються в точках та .

Рівняння дотичної до параболи в точці записується рівнянням:

Рівняння дотичної до параболи в точці записується рівнянням:

Оскільки для кутових коефіцієнтів дотичних і має місце рівність то вони перпендикулярні.

Аналогічно можна показати, що дотичні до парабол, проведені в точці також перпендикулярні.

Отже, параболи перетинаються під прямим кутом.

Механічний спосіб побудови параболи та побудова точок параболи за допомогою циркуля і лінійки

Означення параболи дозволяє вказати спосіб креслення її частини за допомогою лінійки, косинця і нитки.

Нехай задані - фокус і - директриса параболи. Один кінець нитки, довжина якої дорівнює більшому катету косинця, закріплюємо в фокусі, а інший кінець – у вершині гострого кута , протилежного меншому катету. Закріпимо вздовж директриси лінійку і до неї приставимо меншим катетом косинець.

Я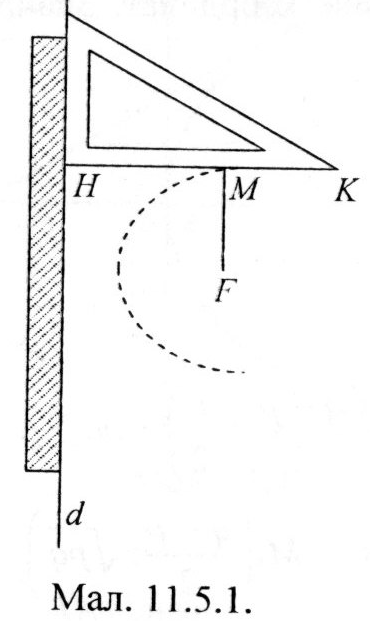 кщо переміщувати косинець вздовж лінійки, утримуючи нитку натягнуту олівцем, то олівець (точка М) буде описувати частину параболи.

Справді, і

Тому

Р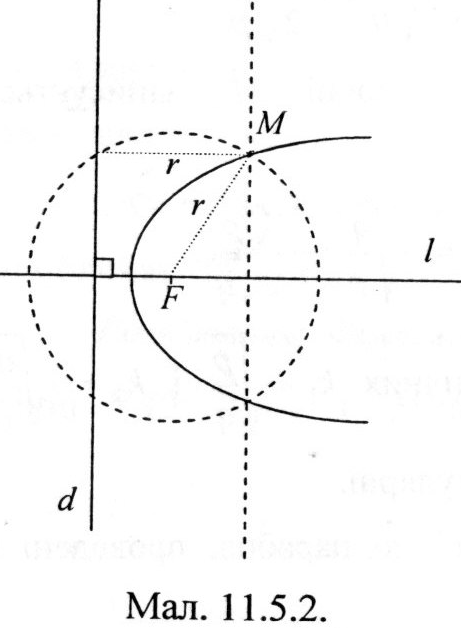 озглянемо тепер спосіб побудови точок параболи, коли задані фокус і директриса, за допомогою циркуля і лінійки.

Проведемо через фокус пряму перпендикулярну директрисі (вісь симетрії параболи). Побудуємо довільну пряму паралельну директрисі. Точки цієї прямої з колом, центр якого міститься в фокусі параболи, а радіус дорівнює відстані від директриси до даної прямої, належать параболі згідно з означенням.