Властивості параболи

Використовуючи канонічне рівняння параболи, вивчимо її найпростіші властивості. З канонічного рівняння параболи бачимо, що вона є алгебраїчною лінією другого порядку.

1.Парабола не містить точок з від’ємними абсцисами, тобто належать півплощині

Справді, - це відстань від фокуса до директриси, отже, число додатне, тому

2.Парабола має вісь симетрії.

Очевидно, що, якщо точка належить параболі то точка симетрична відносно осі теж належить . Тому є віссю симетрії даної параболи.

3. Точка перетину параболи з її віссю називається її вершиною. Вершиною параболи є початок координат.

Вершина розбиває параболу на дві конгурентні частини, кожна з яких називається віткою параболи.

Зауваження. Рівняння, , , , де задають параболу і теж називаються канонічними.

4. Коло з центром у фокусі і радіусом, рівним половині фокального параметра, має з параболою лише одну спільну точку (точніше : дві співпадаючі).

Д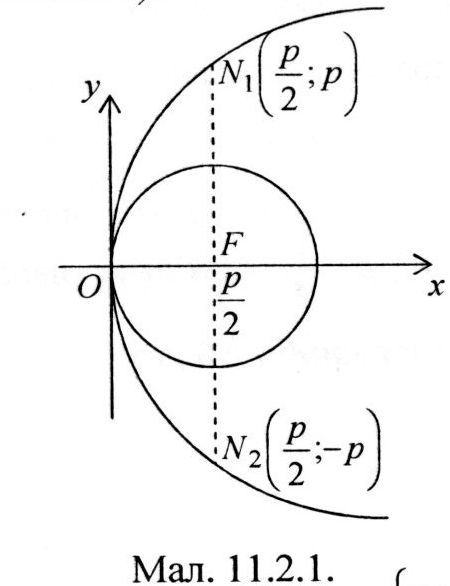 оведення. Коло з центром у фокусі параболи і радіусом задається канонічним рівнянням:

Взаємне розміщення і характеризує система

З неї

Тобто або

На параболі відсутні точки з від’ємними абсцисами, отже, - єдина спільна точка параболи і кола.

5. Пряма є дотичною до параболи . Пряма ( ) перетинає параболу в двох точках.

Доведення. Справді, система рівнянь

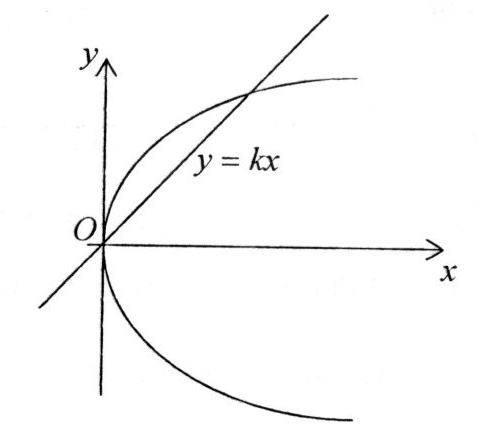
Має два розв’язки:

Задача 1. Парабола визначаються фокусом і директрисою Написати рівняння півплощини, в якій вона лежить.

Розв’язання. Вісь параболи проходить через фокус і перпендикулярна директрисі. Отже,

Знайдемо вершину параболи . З цією метою спочатку визначимо спільну точку директриси і осі параболи:

.

Вершина є серединою відрізка Отже,

Пряма, яка проходить через точку паралельно директрисі є межею шуканої півплощини:

Шуканою півплощиною є , оскільки їй належить точка

Дотична до параболи

Теорема 1. Дотична до параболи в точці , задається рівнянням :

Доведення. Оскільки то Покажемо, що пряма перетинає параболу в двох співпадаючих точках. Для цого розглянемо систему:

З останньої рівності отримаємо:

,

Останнє квадратичне рівняння має два співпадаючі розв’язки.. Отже, пряма перетинає параболу в двох співпадаючих точках, тобто є дотичною. Теорему доведено.

Наслідок. Рівняння дотичної до параболи в точці має вигляд:

, якщо

, якщо

, якщо

Пропонуємо читачеві, використовуючи рівняння дотичної (11.3.1) до параболи і формули перетворення координат, самостійно вивести рівняння дотичної до параболи в точці

Задача 1. Написати рівняння дотичної до параболи в точці

Розв’язання. Рівняння дотичної до даної параболи має вигляд

Оскільки точка належить параболі, то

Відповідь.

Задача 2. Через точку провести дотичну до параболи

Розв’язання. Рівняння дотичної до даної параболи має вигляд:

Знайдемо координати точки дотику

Розв’яжемо систему:

Отже,

Відповідь.

Задача 3. Довести, що до параболи можна провести лише одну дотичну з кутовим коефіцієнтом

Доведення. Дотичну до параболи записується рівнянням: де - точка дотику.

Якщо то дотична записується рівнянням

Якщо то Кутовий коефіцієнт дотичної

Він рівний лише при При цьому Отже існує єдина точка в якій дотична до параболи має кутовий коефіцієнт