Означення та канонічне рівняння параболи
Означення 1. Параболою називається геометричне місце точок площини рівновіддалених від фіксованої точки (фокуса) і заданої прямої (директриси).
Оскільки
параболу визначають задані фокус
і директриса
то відстань між ними вважається заданою.
Її позначатимемо
і називатимемо фокальним
параметром параболи.
Вивчимо
параболу методом координат. З цією метою
виберемо прямокутну Декартові систему
координат так, що б фокус містився на
осі
,
вісь
була
перпендикулярна директрисі, а початок
координат був рівновіддаленим від
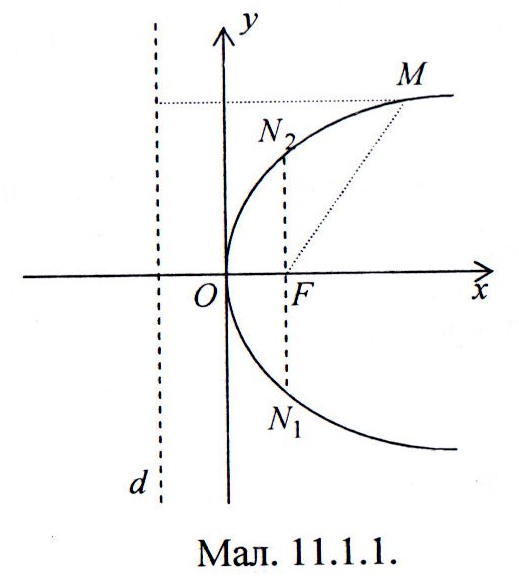
фокуса і директриси (див. мал. 11.1.1). Тоді
фокус
має
координати
,
директриса задається рівнянням
Якщо
- довільна точка параболи, то
що в координатній формі записується:
Отримане рівняння називається канонічним рівнянням параболи. Воно містить лише один параметр , який виражає відстань від фокуса до директриси. Отже, сім’я всіх парабол є одно параметричною.
Фокальним
радіусом точки М
параболи
з фокусом
називається відрізок
(а також його довжина).
Фокальною
хордою параболи називають
хорду, яка паралельна директрисі і
проходить через фокус. Визначимо
координати кінців фокальної хорди
параболи
Оскільки перша їх координата
то для другої координати
Тому
Отже, параметр
- це половина довжини фокальної хорди.
Парабола як геометричне місце точок (фігура, лінія) була відома вже античним математикам і розглядалася як лінія перетину прямого колового конуса площиною, яка не проходить через вершину конуса і паралельна деякій дотичній площині цього конуса.
У
шкільному курсі математики парабола
фігурує в якості графіка квадратичної
функції:
Вона
має фокальний параметр
,
вісь симетрії
вершину
повернута вітками в гору при
і вітками вниз при
.
Задача
1. На
параболі
знайти точки, фокальний радіус яких
дорівнює 6.
Розв’язання. Оскільки шукана точка належить параболі, то її координати задовольняють рівняння .
Фокальний
параметр даної параболи
.
Тому фокус параболи має координати
.
Тоді фокальній радіус:
або
.
Відповідь:
Задача
2. В
прямокутній декартовій системі координат
фокус
параболи
має координати (-2;3), а директриса
записується рівнянням
Скласти рівняння параболи.
Розв’язання.
Оскільки
фокус не лежить на осі
,
то рівняння не є канонічним. Нехай
- довільна точка параболи
.
Тоді, згідно з означенням параболи
,
що в координатній формі переписується:
Після піднесення до квадрату і множення на 25, рівняння матиме вигляд:
Відповідь:
Задача
3. Який
фокальний параметр має парабола, фокус
якої в прямокутній системі координат
має координати (-5;4), а директриса
записується рівнянням
Розв’язання.
Задача
4. Знайти
фокус і директрису параболи
Розв’язання. Переписавши рівняння параболи у вигляді
Бачимо,
що фокальний параметр параболи
Оскільки парабола симетрична відносно
осі
і
міститься у площині
то
і
