Дослідження властивостей гіперболи за її канонічним рівнянням

Використовуючи канонічне рівняння гіперболи (13.1.1), вивчимо її найпростіші властивості.

1. Гіпербола є алгебраїчною лінією 2-го порядку.

2. Обмеженості. З рівняння (13.1.2) слідує, що

Отже в смузі точок гіперболи (13.1.2) немає.

3. Симетрії. Гіпербола має дві взаємно перпендикулярні осі симетрії, точка перетину яких є центром симетрії гіперболи.

Оскільки рівняння (13.1.2) містить змінну лише в квадраті, то гіпербола (13.1.2) симетрична відносно осі . З тих же причин вона симетрична осі . Оскільки з того, що точка М( належить гіперболі (13.1.2), випливає, що їй симетрична відносно початку координат точка належить гіперболі, то гіпербола (13.1.2) симетрична відносно початку координат.

Примітка. Оскільки гіпербола (13.1.2) симетрична відносно осі і в смузі її точок немає, то ця гіпербола складається с двох конкурентних незв’язних частин (віток).

4. Вершинами гіперболи називають точки її перетину осями симетрії. Гіпербола (13.1.2) перетинає вісь симетрій в точках Іншу вісь симетрії, вісь , вона не перетинає.

5. Осі. Числа 2 та 2 називають дійсною та уявною осями гіперболи відповідно, а числа та - дійсною та уявною півосями гіперболи.

6. Неперервність. Виразивши з рівняння (13.1.2) через :

б ачимо симетричність гіперболи (13.1.2) відносно осі і відсутність її точок в смузі Враховуючи симетрії гіперболи (13.1.2), дослідження її властивостей досить проводити в першій чверті, для якої . . З останньої рівності бачимо, що є строго

зростаючою неперервною функцією («малим приростам аргумента відповідають малі прирости функцій»), яка при набуває значення 0. Це означає, що кожна вітка гіперболи є неперервною лінією.

Взаємне розміщення гіперболи і прямої, яка проходить через її центр

Взаємне розміщення гіперболи (13.1.2) і прямої характеризує система:

Звідки

З останньої рівності видно, що:

1 ) при (тобто ) спільних точок немає;

2 )при (тобто або ) пряма перетинає гіперболу в двох точках.

Окремо проаналізуємо випадок тобто

Асимптоти гіперболи

Означення. Пряма називається асимптотою кривої , якщо точка рухаючись по кривій у нескінченність, необмежено наближається до прямої .

Теорема 13.4.1. Кожна гіпербола має дві асимптоти. Якщо гіпербола задана канонічним рівнянням (13.1.2), то її асимптоти виражаються виражаються рівняннями

Доведення. Враховуючи симетрії гіперболи, досить довести, що пряма є асимптотою.

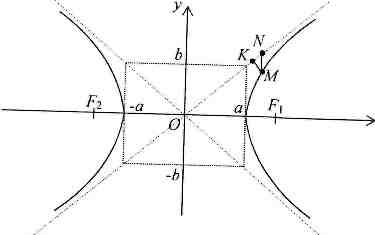
Нехай , , , К – проекція точки М на пряму , - точка перетину прямої з прямою, яка проходить через точку М і паралельна осі .

Що й вимагалось довести.

Ексцентриситет гіперболи.

Ексцентриситетом гіперболи називається число , яке дорівнює відношенню фокусної відстані до довжини дійсної осі гіперболи:

Оскільки 2с>2 , то ексцентриситет гіперболи завжди більше 1.

Ексцентриситет гіперболи є характеристикою форми кривої. Справді,

(13.5.1)

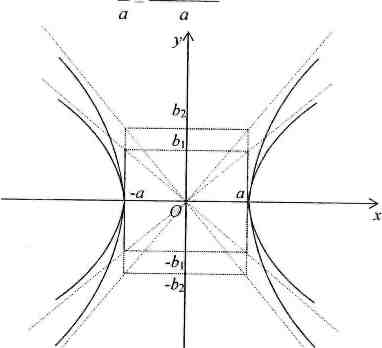
Якщо а — фіксоване, а то , і навпаки, якщо , то

Отже, чим менший ексцентриситет еліпса, тим більше гіпербола «стиснута» до своєї уявної осі. І навпаки, чим більший ексцентриситет, тим гіпербола «витягнутіша» (більше відношення осей).

Гіпербола, півосі якої рівні (а = ) називається рівнобічною. Її рівняння має вигляд х² - у² = а². Оскільки , то . Асимптоти рівнобічної гіперболи задаються рівняннями і , вони взаємно перпендикулярні.

Рівняння гіперболи в прямокутній Декартовій системі координат, осі якої співпадають з її асимптотами, має вигляд

де

Отже, рівнобічна гіпербола є графіком оберненої пропорційності.