Оптичні властивості еліпса Теорема про оптичну властивість еліпса.

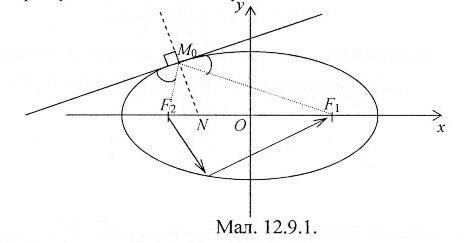
Теорема 12.9.1. Дотична до еліпса утворює однакові кути з фокальними радіусами точки дотику.

Доведення. Враховуючи симетрії еліпса, не порушуючи загальності, можна розглядати точку дотику в другій чверті ( ).

Дотична до еліпса записується рівнянням (12.8.1).

Легко бачити (див. мал. 12.8.1), що вона утворюватиме з фокальними радіусами точки М_а однакові кути тоді і тільки тоді, коли нормаль до еліпса в точці М₀ (тобто пряма, яка проходить через точку М₀ і перпендикулярні дотичній) є бісектрисою трикутника

Напишемо рівняння нормалі і доведемо, що вона є бісектрисою.

Оскільки вектор напряму дотичної є перпендикулярним до нормалі, то рівняння останньої має вигляд:

Знайдемо точку перетину нормалі з віссю Ох. Оскільки у_м =0,

То

Згідно з ознакою бісектриси трикутника, нормаль М₀N є бісектрисою трикутника тоді і тільки тоді, коли:

Доведемо це. Розглянемо

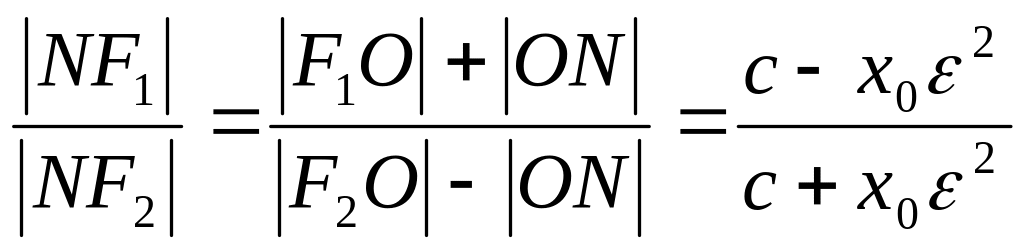
Оскільки то, враховуючи вирази фокальних радіусів (12.4.2),

Отже, - бісектриса, що й вимагалось довести. Теорему доведено.

Фізичний зміст оптичної властивості еліпса: всі промені, що виходять з одного фокуса при дзеркальному відбиванні від еліпса попадають в інший фокус (мал. 12.9.1).

Рівняння еліпса в полярній системі координат (полюс якої знаходить в фокусі , а полярна вісь направлена вздовж великої осі):

де — фокальний параметр еліпса, що дорівнює половині довжини

фокальної хорди (хорди, яка проходить через фокус перпендикулярно великій осі).

2. Означення та канонічне рівняння гіперболи

Означення 1.. Гіперболою називається геометричне місце точок площини, модуль різниці відстаней яких від двох фіксованих точок (фокусів) є величиною сталою і меншою відстані між фокусами.

Я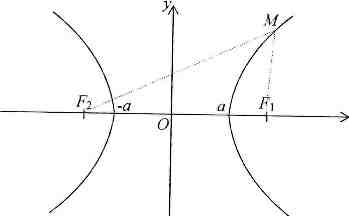 кщо F1 і F ₂ є фокусами гіперболи у, то відстань між ними

[F1F2]= 2с називається

фокусною відстанню.

Якщо М — точка гіперболи у. то відстані r1 |F1M|, r2 |F2M| називаються фокальними радіусами точки М.

Згідно з означенням гіперболи:

Мал. 13.1.1,

||F1M|-|F2M|| 2a=const,

Причому 2а < 2с.

Вивчимо гіперболу методом координат. З цією метою виберемо

прямокутну декартову систему координат так, щоб фокуси знаходились на

осі Ох і були симетричними відносно початку координат (див. мал. 13.1.1).

Тоді F1(с;0), F₂(-с;0). Якщо М(х;у) — довільна точка гіперболи, то

|F1M | - |F2M|= ±2а, що в координатній формі записується:

Поклавши

отримаємо:

Поділивши обидві частини рівності на (оскільки , то ), отримаємо:

(13.1.2)

Рівняння (13.1.2) називається канонічним рівнянням гіперболи. Рівність (13.1.1) називається основним співвідношенням між параметрами гіперболи.

Задача 1 Знайти фокальні радіус-вектори точки А гіперболи

Розв’язання. Переписавши рівняння гіперболи у канонічному вигляді:

Знаходимо Тоді . Отже, - фокуси гіперболи. Фокальні радіуси точки А:

Задача 2. Знайти координаті фокусів гіперболи

Розв’язання. Зрівняння гіперболи Використовуючи основне співвідношення між параметрами гіперболи, знаходимо

Отже, с=4

Відповідь: