
- •Означення та канонічне рівняння еліпса
- •Дослідження властивостей еліпса за його канонічним рівнинним
- •Директриси еліпса. Теорема про фокальні властивості еліпса
- •Параметричні рівняння еліпса
- •Побудова точок еліпса за допомогою циркуля та лінійки
- •Дотична до еліпса.
- •Оптичні властивості еліпса Теорема про оптичну властивість еліпса.
- •Означення та канонічне рівняння гіперболи
- •Дослідження властивостей гіперболи за її канонічним рівнянням
- •Взаємне розміщення гіперболи і прямої, яка проходить через її центр
- •Асимптоти гіперболи
- •Ексцентриситет гіперболи.
- •Вираз фокальних радіусів точки гіперболи
- •Директриса гіперболи. Теорема про фокальні властивості гіперболи
- •Побудова точок гіперболи за допомогою циркуля та лінійки
- •Дотична до гіперболи
- •Оптичні властивості гіперболи. Теорема про оптичну властивість гіперболи.
- •Означення та канонічне рівняння параболи
- •Властивості параболи
- •Дотична до параболи
- •Оптична властивість параболи
- •Механічний спосіб побудови параболи та побудова точок параболи за допомогою циркуля і лінійки
Змістовий модуль 5. Криві другого порядку. Загальна теорія кривих другого порядку.
Лекція № 12. Еліпс, гіпербола, парабола, їх канонічні рівняння і властивості.
Означення та канонічне рівняння еліпса
Означення12.1.1. Еліпсом називається геометричне місце точок площини, сума відстаней яких від двох фіксованих точок (фокусів) є величиною сталою і більшою відстані між фокусами.
Я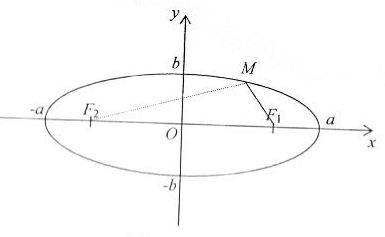 кщо
кщо
![]() і
і
![]() є фокусами еліпса
є фокусами еліпса
![]() ,
то відстань між ними
,
то відстань між ними
![]() називається фокусною
відстанню.
називається фокусною
відстанню.
Якщо М – точка еліпса , то відстані
![]() називаються
фокальними
радіусами точки М.
називаються
фокальними
радіусами точки М.
Згідно з означенням еліпса:
Мал. 12.1.1.
![]()
Причому
![]() .
.
Вивчимо
еліпс методом координат. З цією метою
виберемо прямокутну Декартові систему
координат так, щоб фокуси містились на
осі
![]() і були симетричними відносно початку
координат (див. мал. 12.1.1.). Тоді
і були симетричними відносно початку
координат (див. мал. 12.1.1.). Тоді
![]()
![]()
![]() Якщо
Якщо
![]() - довільна точка еліпса, то
- довільна точка еліпса, то
![]() що в координатній формі записується:
що в координатній формі записується:
![]()
![]()
![]() ,
,
![]()
![]()
![]()
Поклавши
![]() отримаємо:
отримаємо:
![]()
Поділивши
обидві частини рівності на
![]() (оскільки
(оскільки
![]() то
то
![]() ),
отримаємо:
),
отримаємо:
![]() (1)
(1)
Рівняння (1) називається канонічним рівнянням еліпса.
Задача 1 Вершина трикутника, що має нерухому основу, переміщується так, що периметр трикутника зберігає постійну величину. Знайти траєкторію вершини трикутника, при умові, що основа має довжину 24см, а периметр дорівнює 50см.
Розв’язання.
Нехай
А
і В
–
нерухомі, а М
–
рухома вершини трикутника. За умовою
![]() і
і
![]() звідки
звідки
![]() .
.
Отже,
траєкторію точки М
є
геометричне місце точок, сума відстаней
яких від точок А
і
В
є
величина стала і більша відстані між
цими точками (26>24), тобто є еліпсом з
довжиною великої осі
![]() фокусною
відстанню
фокусною
відстанню
![]() і довжиною малої осі
і довжиною малої осі
![]()
Задача
2. Еліпс
проходить через точки
![]() і
і
![]() Скласти рівняння еліпса, якщо відомо,
що його осі лежать на осях координат.
Скласти рівняння еліпса, якщо відомо,
що його осі лежать на осях координат.
Розв’язання.
Оскільки
осі еліпса лежать на осях координат, то
його рівняння має вигляд: ![]()
![]()
![]()
![]()
![]()
![]()
Покладемо
![]() і розв’яжемо систему рівнянь:
і розв’яжемо систему рівнянь:
![]()
![]()
![]()
Отже,
![]() і канонічне рівняння еліпса має вигляд:
і канонічне рівняння еліпса має вигляд:
![]()
Відповідь:
Задача
3. Дано
рівняння еліпса
![]() Обчислити довжини його осей, координати
фокусів.
Обчислити довжини його осей, координати
фокусів.
Розв’язання. Перетворимо рівняння еліпса поділивши обидві його частини на 4225;
![]()
В
отриманому канонічному рівнянні бачимо,
що
![]() -
велика піввісь, а
-
велика піввісь, а
![]() - мала піввісь еліпса. Із основного
співвідношення параметрами еліпса
- мала піввісь еліпса. Із основного
співвідношення параметрами еліпса
![]() отримуємо
отримуємо
![]()
Отже, фокуси і мають координати (12;0) і (-12;0).
Відповідь: 2а=26 – довжина великої осі;
2b=10 – довжина малої осі;
![]()
Механічний спосіб побудови еліпса
Означення еліпса дозволяє вказати простий спосіб його побудови. Зафіксуємо дві точки , і , — фокуси еліпса. Закріпимо в цих точках нитку довжиною 2а більшою, ніж відстань між ними. Якщо відтягнути нитку олівцем, і рухати його, тримаючи весь час нитку натягнутою, то можна накреслити еліпс з даними фокусами , і F2 та довжиною великої осі 2а.
Дослідження властивостей еліпса за його канонічним рівнинним
Використовуючи канонічне рівняння еліпса (12.1.1), вивчимо мої о найпростіші властивості.
Властивість 1. Еліпс є алгебраїчною лінією 2-пі порядку.
Властивість 2. Еліпс є обмеженою фігурою.
![]() З
канонічного рівняння еліпса маємо
З
канонічного рівняння еліпса маємо
Звідки
бачимо, що еліпс належить прямокутнику
з вершинами Mt(a;b),

![]()
![]()
Властивість 3. Еліпс мас дві взаємно перпендикулярні осі симетрії.
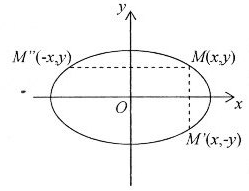 Очевидно,
що коли точка
Очевидно,
що коли точка
![]() належить еліпсу у,
то
й М'(х,-у)
належить еліпсу у,
то
й М'(х,-у)![]() ,
тобто
еліпс у
симетричний
відносно осі Ох.
Аналогічно,
якщо
,
тобто
еліпс у
симетричний
відносно осі Ох.
Аналогічно,
якщо
![]() то
й
то
й
![]()
тобто еліпс у симетричний відносно осі Оу.
Властивість 4. Еліпс — центрально-симетрична фігура.
Оскільки
М(х.у) є у => М'(-х,-у) ,
то еліпс, заданий рівнянням (12.1.1), симетричний відносно початку координат.
Зауваження. Властивість 4 є наслідком властивості 3, оскільки фігура, що мас дві взаємно перпендикулярні осі симетрії, є симетричною відносно точки їх перетину.
Вершинами еліпса називаються точки перетину еліпса з його осями симетрії.
Властивість
5.
Вершинами еліпса (12.1.1) Є
точки
![]() ,
,
![]() ,
В,(0;Ь),
В2(0-Ь)
(див.
мал. 12.1.1).
,
В,(0;Ь),
В2(0-Ь)
(див.
мал. 12.1.1).
Число
2а
є
довжиною відрізка
![]() (великої осі еліпса), число
(великої осі еліпса), число
![]() довжиною відрізка В{В2
(малої осі еліпса).
довжиною відрізка В{В2
(малої осі еліпса).
Властивість 6. Еліпс є неперервною замкненою кривою.
Канонічне рівняння еліпса можна переписати у вигляді:
![]()
Звідки бачимо, що малим приростам х відповідають малі прирости у.
В
першій чверті еліпс є неперервною
лінією, що з'єднує точки
![]() і
і
![]() . Оскільки він симетричний відносно
осей Ох
та
Оу,
то
частинка еліпса, що міститься в четвертій
чверті, конгруентна частинці в першій
чверті і з'єднує
точки
. Оскільки він симетричний відносно
осей Ох
та
Оу,
то
частинка еліпса, що міститься в четвертій
чверті, конгруентна частинці в першій
чверті і з'єднує
точки
![]() і.
Аналогічно отримуємо, що еліпс складається
з чотирьох конгруентних частинок, які
з'єднують точки
і
,
і
і.
Аналогічно отримуємо, що еліпс складається
з чотирьох конгруентних частинок, які
з'єднують точки
і
,
і
![]() ,
В2
і
А2,
,
В2
і
А2,
![]() і
відповідно.
і
відповідно.
Задача
1.
На еліпсі
![]() знайти точки, розміщені на
знайти точки, розміщені на
відстані 5 одиниць від його малої осі.
Розв'язання. Даний еліпс заданий канонічним рівнянням, а отже, симетричний відносно обох координатних осей. Оскільки 24<30, то велика вісь і фокуси даного еліпса знаходяться на осі Оу, а мала вісь на осі Ох.
Якщо М(х;у) — шукана точка, то
![]() тобто
тобто
![]()
Знайдемо
![]()
![]()
![]()
Відповідь:
![]() (2;5),
(2;5),
![]() (-2;5),
(-2;5),
![]() (-2;-5),
(-2;-5),
![]() (2;-5).
(2;-5).
Задача 2. Вказати осі симетрії еліпса х2+3у2+ 4х-18 + 4 =0.
Розв’язання. Перетворимо рівняння еліпса:
![]()
![]()
Заміна
х+2
на
![]() ,
у-3
на
у',
яка
рівносильна перетворенню координат
перенесенням початку в точку
,
у-3
на
у',
яка
рівносильна перетворенню координат
перенесенням початку в точку
![]() ;
;
![]()
Приводить
до рівняння: ![]()
В новій системі координат еліпс симетричний відносно координатних осей, які в старій системі координат задаються рівняннями:
х = -2, у=3.
Відповідь: х=-2, у = 3 – осі симетрії даного еліпса.
Зауваження. Якщо центр еліпса знаходиться в точці С(.x0; y0), а велика і мала осі паралельні осям координат, то його рівняння в прямокутній декартовій системі координат має вид:
![]() (12.3.1)
(12.3.1)
Ексцентриситет еліпса. Вираз фокальних радіусів точки еліпса
Ексцентриситетом
еліпса називається
число
![]() ,
яке
дорівнює відношенню фокусної відстані
до довжини великої осі еліпса:
,
яке
дорівнює відношенню фокусної відстані
до довжини великої осі еліпса:
![]()
Оскільки 2с < 2а, то ексцентриситет еліпса задовольняє нерівності
![]()
причому
![]() 0,
коли
2с =
0, тобто
коли
0,
коли
2с =
0, тобто
коли
![]() і
еліпс є колом.
і
еліпс є колом.
Ексцентриситет еліпса є характеристикою форми кривої. Справді,
![]()
![]() ,
,
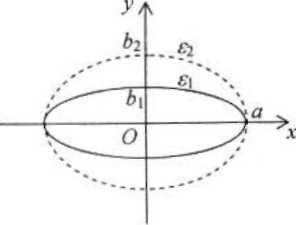
Якщо
а
–
фіксоване,
а
![]() ,
то
,
то
![]() ,
і навпаки, якщо
,
і навпаки, якщо
![]() ,
то
,
то
![]() .
.
Отже, чим менший ексцентриситет еліпса, тим більше еліпс «схожий» на коло (відношення осей ближче до 1). І навпаки, чим більший ексцентриситет, тим еліпс «витягнуті ший» (менше відношення осей).
Задача 1. Меридіан земної кулі має форму еліпса, відношення
осей
якого дорівнює
![]() .
Визначити ексцентриситет земного
меридіана.
.
Визначити ексцентриситет земного
меридіана.
Розв’язання:
![]() .
.
Відповідь:
![]()
Лема
1. Фокальні
радіуси
![]() і
і
![]() точки
точки
![]() еліпса
еліпса
![]() з ексцентриситетом
виражаються наступним чином:
з ексцентриситетом
виражаються наступним чином:
(![]() 12.4.2)
12.4.2)
Доведення. Згідно з означенням еліпса
![]()
Виразимо різницю:
![]() .
.
Розглянемо систему рівнянь:
![]()
![]()
Звідки
![]() і
і
![]()
Що й вимагалось довести.
Задача
2. На
еліпсі
![]() знайти точку,
відстань якої від
правого фокуса в
чотири рази більше відстані від лівого
фокуса.
знайти точку,
відстань якої від
правого фокуса в
чотири рази більше відстані від лівого
фокуса.
Розв'язання. Оскільки за умовою а=10, b=6, то ексцентриситет
![]()
Нехай
М(х,у)
—
шукана точка
![]() — її фокальні радіуси. За умовою
— її фокальні радіуси. За умовою
![]() Використовуючи
вирази фокальних радіусів (12.4.2), маємо:
Використовуючи
вирази фокальних радіусів (12.4.2), маємо:
![]()
Звідки
![]() .
А
отже,
.
А
отже,
![]()
Відповідь:
![]()
