
Шпаргалки за 1-ый курс 1-ый семестр / 2008-03-03-21-34-Сашенька-
.doc|
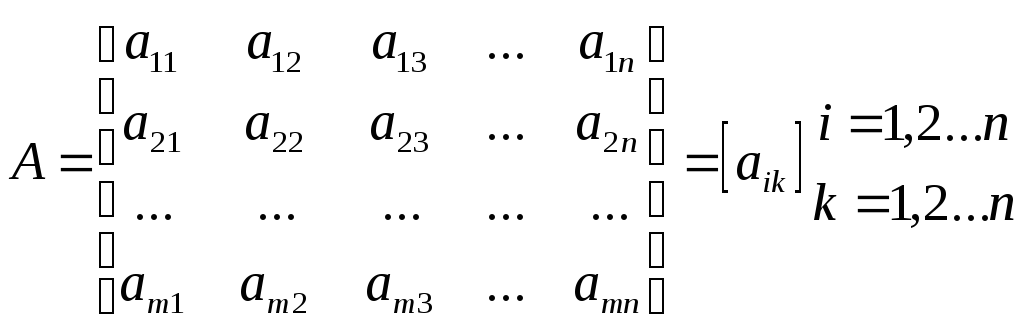
1.Матрицы. Действия с матрицами. Матрицы – это система из m×n элементов какого-либо поля К расположенных в виде поля прямоугольной таблицы содержащей “m” точек и “n” столбцов.
Если m=n, то А называется квадратной
Равенство матриц. Две матрицы называются равными, если они одинаковой размерности и числа, стоящие на одинаковых местах совпадают. А=В если: 1) А(m×n); В(m×n) 2)аij=bij i=1,2...m j=1,2...n
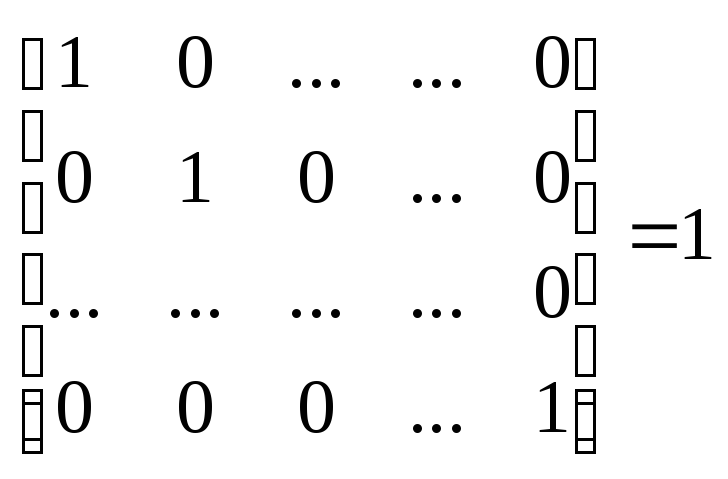
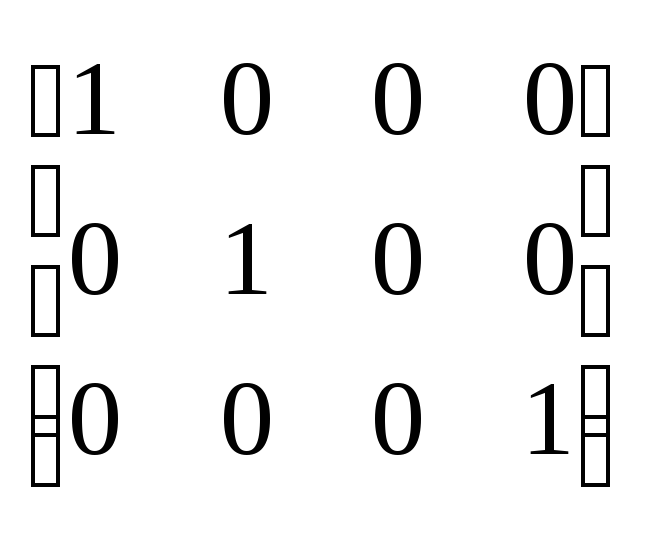
E(единичная) Это квадратная матрица, у которой по диагонали стоят единицы, остальные нули.
|
С=А-В=А+(-В) 3)Умножение
Умножение матриц возможно, только если размерности матриц согласованы.
Число столбцов 1 сомножителя должно равняться числу строк 2ого.
Произведение двух матриц зависит от порядка сомножителей, т.е. если АВ определено, то ВА может не иметь смысла если А и В (квадратные), то тогда опред. АВ и ВА но не обязательно они равны, если АВ=ВА, то эти матрицы наз. перестановачные.
Сумма произведений диагональных матриц есть новая диагональная матрица.
Транспонирование.
Свойства: |
2.Системы линейных уравнений. Метод Гаусса-Жордана.
Набор значений
Равносильные системы ур-й – это такие системы, решения которых совпадают.
Метод Гаусса-Жордана. Будем рассматривать следствие равносильного преобразования |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
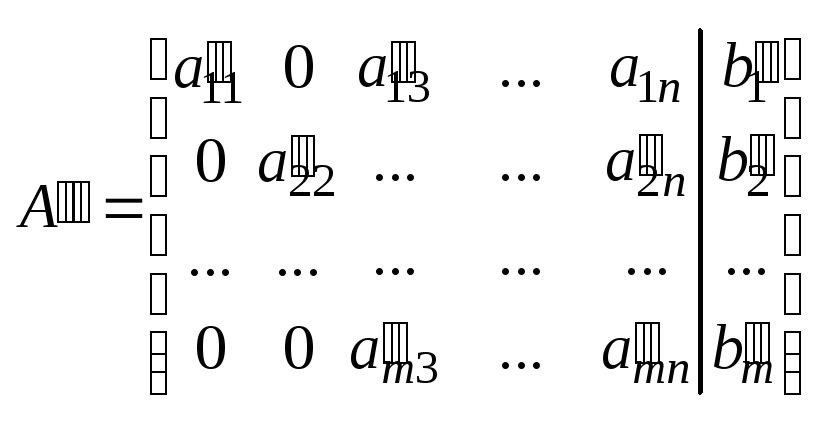
Удобно коэффициент при x1 иметь равным единице. Метод полного исключения – это алгоритм, который через конечное число шагов либо установит отсутствие решений у системы, либо приводит ее к равносильной системе одного из следующих типов: 1) m=n
2) m<n
Бесчисленное множество решений 3) нет решений
Алгоритм Гаусса-Жордана. 1ШАГ. 1) В матрице системы выбираем ведущий элемент(наибольший по модулю0, переставляя строки и |
3.Определитель квадратной матрицы. Св-ва определителей. 1) Пусть А - кв. матр. порядка n=1. A = [a11]. Назовем число а11 определителем матрицы А, обозначим его det A=a11 2)
n=2
3) n>2 det
A =
Mij- определитель матрицы, полученный из матрицы А вычеркиванием i-ой строки из j-ого столбца. Mi j - наз. минором элемента Ai j. Aij – наз. алгебраическим дополнением элемента аij Свойства определителей. 1.
det
A = Aij=(-1)i+jMij
2.
det
A = det A= det AТ Метод матричной индукции n=2 det
A
=
det
AТ= |
(столбца), то определитель меняет знак на противоположный. 7. Определитель не изменяется, если к элементу любой строки (столбца) прибавить соотв. Элементы др. строки (столбца) умноженное на одно и тоже число λ..
detA'=detA Доказательство по св-вам 4,5. 8.
i ≠ k det
A= Пусть элементы 2-ого столбца умножаются на алгебраические дополнения элементов 1-ого столбца. a12A11+a22A21+a32A31=0 т.к.
Аij
не
зависит от аij
,то
для любых x,y,z
можно записать x=a12 y=a22 z=a32 тогда
С другой стороны, Δ=0 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
4. Вычисление определителей. 1)
det 2)
det
I= 3)
(верхняя треугольная) 4)
(нижняя треугольная) 5)
|
5. Прямая и обратная теорема Крамера. Если detA≠0, то матрица наз. невырожденной a11x1+a12x2+...+a1nxn=b1 a21x1+a22x2+...+a2nxn=b2 ... an1x1+an2x2+...+annxn=bn A= Если матрица линейной системы невырождена, то система 1 имеет единственное решение. (2)
Δ-определитель матрицы, составленный из коэффиц. Δk-определитель, который получается из Δ заменой k-ого столбца на столбец свободных членов. Док-во. 1) Возьмем систему (1) 1-ое ур-е умножим на А11, 2-ой на А21 и т.д. и почленно сложим ур-я.
(a11A11+a21A21+...+an1An1)x1+(a21A11+a22A21+... +an2An1)x2+(a1nA11+a2nA21+...+annAn1)xn=b1A11+b2A21+...+bnAn1 det A x1= Δ 1 Δ
1= |
7.Матричные уравнения: AX=D; XA=B. Если в однородной системе число ур-й меньше числа неизвестных, то система имеет ненулевые решения(бесконечное мн-во решений) Ax=B
Операция транспонирования. xA=B (xA)T=BT ATxT=BT
(xT)T=x
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
систем
Эти преобразования равносильности системы. Рассмотрим систему (1). В системе 1 найдется хотя бы одно уравнение, в котором коэффициент при X1≠0. Пусть это будет коэффициент a11≠0
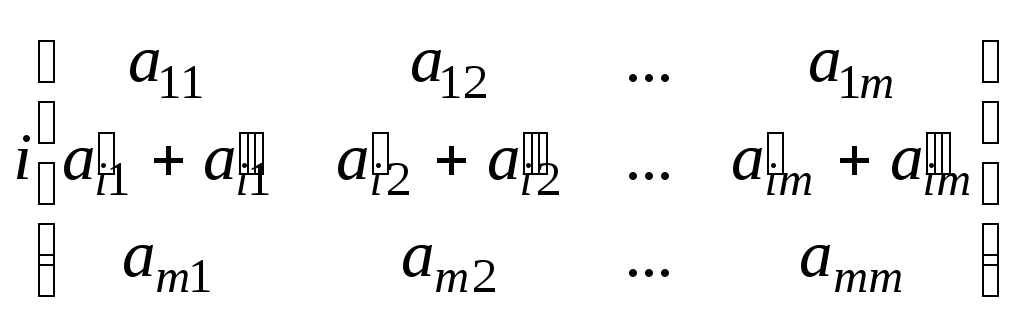
1 ШАГ. Чтобы исключить x1 из 2-ого уравнения системы 1,мы 1-ое уравнение умножим на a21,а 2-ое уравнение на a11 и из 2-ого вычтем 1-ое. После 1-ого шага матрица А' преобразуется в матрицу А''
2 ШАГ. |
|
Вещественные матрицы – у которых все числа вещественные. Действия с матрицами. 1) Умножение матрицы на число
2) Сложение матриц.
1.A+B=B+A 2.A+(B+C)=(A+B)+C 3. 4. 5. 6.(-1)A=-A 7. Если
(Одинаковой размерности) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
тогда
9.det(AB)=detA detB
|
3. Если матрица имеет нулевой столбец или строку, то определитель ее равен нулю. aij=0, j=1,2...n (i=1,2...n) det A=0 4.
A'= A= detA= detA'+detA'' detA= 5.
detA'=λdetA detA'= det(λA)= λndetA Все свойства равноценны для строчек и столбцов. 6. Если в определителе поменять местами любые 2-е строчки |
столбцы расширенной матрицы системы , помещаем ведущий элемент в 1-ую строку и в 1-ый столбец. Делим элементы полученной матрицы на ведущий элемент. 2) Ко 2-ой строке расширенной матрицы прибавляем 1-ую умноженную на “-a21”,к 3-ей строке прибавляем 1-ую умноженную на”-a31” 3) Если в рассмотренной матрице системы образуется строка вида 0 0 ... 0 |b? B≠0, то система не совместна, алгоритм заканчивается. Если какая-то строчка расширенной матрицы принимает вид 0 0 ... 0| 0 , то эта строчка отбрасывается. Если в результате 1 шага не обнаруживается несовместимость, число строк матрицы>1, то переходим ко второму шагу. 2ШАГ. Вычеркнем (мысленно) в расширенной матрице 1 строчку, 1 столбец и в ост. матр. Находим ведущий элемент, переставляя строки и столбцы расш. матр. во 2-уя строчку во 2-ой столбец делим 2-ую строчку на ведущий элемент. К
1-ой строке прибавляем 2-ую строку,
умноженную на “-a32”.
В результате 2-ой столбец примет вид: Повторим пункт 3 из 1-ого шага. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
8. Обратная матрица. Условия существования. Вычисление. Ax=I YA=I I.
II.
X=
[xi
j]
= Опр-е: Ранг матр. это наибольшее из порядков опред. Среди опр-лей порядка r составленных из матрица А таких, что среди них найдется хотя бы один неравный нулю, но все опр-ли порядка r+1 и выше или равны нулю или не могут быть составлены опр-ль нулевого порядка=1 A=
Если матрица нулевая, то ранг = 0 Теорема: если хотя бы один из определителей порядка r , сост. Из матр. r≠0 и все опред. пор. r+1 сост. из матр. А равны нулю, то ранг равен r. Теорема: Ранг матрицы не изменится при элементарных преобразованиях. A→C1→C2→...→B rang A = rang B Замечание: ранг матрицы не измен. Если к ней приписать (строчку) столбец состоящий из нулей. При вычислении ранга матрицы стоит переходить от миноров меньшего порядка,если наеден минор порядка к, то требуется вычисление минора рангом к+1 |
Формула 2 не эквивалентна система 1. Подставим Xк в уравнение системы
если i=j то это будет определитель detA если i≠j то мы получим ноль
Прямая терема доказана. Если система (1) имеет ед. решение, то определитель Ф равен нулю. Допустим, для решения системы мы пременем метод Гаусса. [A/B]→[I/x] detI≠0 detA≠0 т. Крамера не решает вопрос когда опред. А=0, нет решений или их бесконечно много.
|
6.Однородные системы линейных уравнений.
Однородная система всегда имеет нулевое(тригональное)решение. Однородная система всегда совместна. Однородная система имеет одно решение, если число ур-й равно числу неизвестных и опр-ль не равен нулю. Однородная система в которой число ур-й равно числу неизвестных или не имеет нулевого решения тогда и только тогда, когда опр-ль равен нулю.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
9. Линейное векторное пространство, аксиомы. Пространства Rn и Сn. Опр-е. Мн-во L наз. лин. пространств., если 1)к
каждым 2-м элементам x,y 2)если
каждому x Указанные операции должны уд. след. аксиомам.
Теорема Для любого линейного пространства справедливы след. утв-я:
Д-во: пусть сущ. 2 нулевых элемента θ1 и θ2 θ1+ θ2= θ1 если x= θ2 θ2+ θ1= θ2 сл-но θ1= θ2 2) -x эл. противопол. X из мн-ва L – единственен. 3) для любого x из мн-ва L – произв – е нулевого эл. на x дает нулевой элемент. 4)
для любого
|
Пусть
λ
λ
1)
2)
( 2а)
3)
λ ( 4)
(α+β)
5)
α ( Мн-во всех n-мерных вектрорв, с устан. В нем операциях сложения и умножения на хисло образуют комплексное линейное пространство, кот. обозн. Cn. |
10.Линейная зависимость векторов. Свойства. Пусть
даны n-векторы
Линейная
комбинация векторов
Если
имеет место равенство (1), то мы говорим
что в разложении по векторам
Ур-е (2) все будут иметь нулевое решение, т.е. с1,с2, ст=0,но может иметь не нулевое. Опр-е:
мн-во векторов
Векторы
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Пусть
det A≠0
Эта система однородна и имеет единственное решение когда detA≠0 .И это ед. решение нулевое. Опр-е: Линейное пространство C(R) наз. n-мерным, если в нем сущ. n- линейно незав-мых в-ров и нет большего числа линейно незав. в-ров.
|
11.Базис. Разложение вектора по базису. Опр–е:
в пр-ве
Теорема: каждый в-р i из n- мерного пр-ва можно представить как линейную комбинацию базисных в-ров, это разложение единственно. Д-во:
пусть
det A≠0
Если
Базис
Базисов в пр-ве бесконечно много. Теорема. В
пр-ве
Д-во: (от противного) |
12. Скалярное и векторное пр-я. Св-ва. Опр-е:
Скалярным пр-ем 2-х не нулевых в-ров
Если хотя бы один из в-ров =0, то скал-е пр-е =0.
Св-ва.
2)
4)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Однородность скалярного произведения. Для
любых векторов
Ск. пр-е обладает св-вом однородности по каждому из сомножителей. 6)Аддетивность скал. пр-я.
Векторное пр-е. Векторным
пр-ем в-ров
1)
2)
Длина вектора
|
Св-ва:
а)
пусть
Эти векторы
перпендикулярны пл-ти в кот. лежат
Э б)
Если
Векторы
коллинеарные и напр-ны в др. сторону
в кот. напр.
|
13. Смешанное пр-е. Св-ва. Смеш.
Произв. Упоряд. Тройки векторов
([
Св-ва. 1) При перестановке двух сомножителей смеш. пр-е меняет знак:
2)
Векторы
Если
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2вектора
линейнозависимы, если их компоненты
пропорциональны. Если вектора
коллинеарны, то они линейнонезависимы.Система
векторов
Д-во:
I.
Сi
≠ 0
II.
Св-ва.
|
|
Векторное n пространство. Пусть n фиксированное число, упорядоч. сист. n-чисел вида
Векторы
Суммой векторов
(
Противоположный
вектор вектору
Существует нулевой
вектор
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
5) Ф-ма ск-ого пр-я в декартовой системе координат. Пусть в пр-ве фиксировано пр-е не коллин. В-ров, общее начало
По т. Косинусов
Пусть
|
Пусть
Мн-во
векторов т.е.
|
Опр-е:
Если в пр-ве C(R)
сущ. n-лин.незав.
в-ров из пространстваR(C) есть их лин. комбинация,то мы говорим,что пространствоC(R) - n-мерно. Опр-е: Если для любого натур. n в лин. пространстве R(C) сущ. упорядоченное мн-во сост. из. n линейно незав. в-ров, то лин. пр-во n- бесконечно мерно.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
2.
) Ф-ма в-ого пр-я в декартовой системе координат. Пусть
= =
Сл-е
1. Для того, чтобы в-ры
Сл-е 2.
|
3)
Три вектора лежащие в одной плоскости, наз. компланарными. Два в-ра линейно зависимых в-ра наз. коллинеарными. 1 2.
3.
4.
Векторы
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
14.Плоскость и прямая в R3. Общим ур-ем плоскости наз. линейное ур-е Ax + By + Cz +D = 0 (1) где A2+B2+C2≠0. Любая пл-ть в пр-ве опр-ся ур-ем вида (1). Если D = 0, то пл-ть проходит через начало координат; если C = 0 (соответственно A=0 или B=0 ), то пл-ть параллельна оси z (соответственно оси x и ли оси y). Уравнение Ax+D=0 определяет пл-ть , параллельную пл-ти yOz. Положение
плоскости P
в пр-ве полностью определяется точкой
M0(x0,y0,z0),
лежащей на этой пл-ти, и перпендикулярным
ей в-ром
A (x – x0) + B (y – y0) + C (z – z0) = 0 (2) Уравнение
пл-ти, проход. через т. M0(x0,y0,z0)
и параллельной двум неколлинеарным
в-рам
Ур
– е пл-ти, проходящей через 3 данные
точки M1(x1,y1,z1),
M2(x2,y2,z2),
M3(x3,y3,z3),
не лежащие на одной прямой, имеет вид
A
(x
– x1)
+ B
(y
– y1)
+ C
(z
– z1)
= 0, где A,
B,
C
– координаты вектора
Взаимное расположение 2х пл-тей. Угол
A1 x + B1 y + C1 z +D1 = 0 (плоскость P1) A2 x + B2 y + C2 z +D2 = 0 (плоскость P2) равен
углу между ин нормальными в-рами
|
Если все координаты направляющего вектора не равны нулю, прямая может быть также задана след. каноническими ур-ями:
Углы
Прямая, проходящая через две данные точки M1(x1,y1,z1), и M2(x2,y2,z2), представляется ур-ями
Если
прямая
Прямая и пл-ть в пр-ве Угол
|
15. Скалярное пр-е в линейномвекторном пр-ве. Неравенство Коши –Буняковского. в R3
Опр.
В пр-ве Сnскал.
пр-ем в-ра
Св-ва. 1)
2)
3)
4)
5)
6)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
16. Норма в линейном векторном пространстве.
Св-ва: 1)
Для любого
2)
3)Неравенство Минковского (н-во тругольника)
Норма несвязанная со скал. произв-ем. Опр.
Пусть в пр-ве
|
17. Матрица Грамма.
Св-ва: 1)
(Эрметого
(компл. числа)), тогда
2)
|
18. Ортогональный и ортонормированный базисы Коэффициенты Фурье Опр.
векторы
Т.: любое мн-во ненулевых попарно ортогональных в-ров линейно независимо. Д-во:
Сост. линейную комбинацию векторов
Ci=0 i=1,2...m Умножим
(1) ,
Умножим
(1) на c2=0 c1=c2=...=cm=0
Упорядоченный набор из n-векторов попарно ортогональных, не нулевых, явл. ортогон. базисом соотв. пространства. В любом Эвллидовом пр-ве сущ. ортогональный базис. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Ск – коэффициент Фурье разложения вектора х по ортогональному базису ак. Если
|
не нулевые решения
Теорема: Собственные векторы матрицы, соотв. ее попарно различных собств. числам лин. незав. Д-во:
Применем к этому равентву кв. матрицу А.
Умножим
(1) на
вычтем из (2)-(3)
|
22. Собственные числа и собственные векторы самосопряженной матрицы. Опр. Кв. мант. Ф наз. самосопр. если
Если матр вещ. и самрсопряж., то А=АТ, то такие матрицы на. симметрическими. Лемма:
Сл.
А- самосопр. (Эрмитова)
Все собств. числа сопр. матр. Теор.
Собств. в. самос. матр. соотв. само собственным числам ортогональны
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Неравенство Коши-Буняковского
1)
2)
Рассмотрим:
т.к.
Особенности скал. пр-я в Rn
|
Условие
параллельности прямой и пл-ти:
Условие
перпендикулярности прямой и пл-ти:
Каноническое
уравнение прямой
Уравнение
пл-ти
с
направляющим в-ром
Для нахождения координат точки пересечения прямой и прлоскости необходимо решить систему ур-й, состоящую из ур-я пр-мой и ур-я пл-ти.
|
соотношением
Условие
параллельности пл-тей: P1
|| P2
тогда и только тогда,когда коллинеарны
нормальные в-ры
Условие
перпендикулярности пл-тей: P1
Прямая в пр-ве. Каждая пр. в пр-ве может быть задана системой 2х лин. ур-й
(эти ур-я опред. две пл-ти ,пересечением кот. служит данная прямая). Положение
прямой
где
параметр
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Опр.
Вектор
Св-ва ортогональности векторов сохраняется при их нормированности.
Пусть
векторы
Упорядоченный
набор векторов
Пусть
|
Матрица
Грамма :
Т.1 Если система векторов явл. бвзисом, тогда detG≠0. Т.2 Определитель Грамма любого базиса положителен. Т.3 Если базис ортонормирован, то его матрица Грамма единична
|
Аксиома: 1)
2)
3)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Сл-е:Если
все собств. числа
самосопр.
матрицы,то соотв. им собств. векторы
Теорема: Любая самосопряженная матр. всегда имеет собств. ортог. базис, т.е. базис сост. из собств. поперноортог. векторов соотв. ее собств. числами. А:
Если
каждый собственный вектор
ортонормированный, то получ. собств.
ортогон. базис.
|
Умножим
(4) на
т.к.
все собств. числа
Значит
|
21.Собственные числа и собственные векторы матрицы. Пусть
дана кв. матрица А разм. n×n,
Рассмотрим
Опр. Если для кв. матр. А и не нулевого вектора
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
23. Подобные матрицы. Собств. числа с собств. векторы подобных матриц. Две матрицы одинаковой размерности, на. подобными, если сущ. невырожденной матр. S такая, что В=S-1АS
Если А подобна В , В подобно С, то А подобно С.
Т. Подобные матрицы имеют одинаковый набор собственных чисел
Характеристический многочлен
|
25.Квадратичные формы. Приведение к каноническому виду А- симметрическая матрица, АТ=А (А-веществ)
Геометрическая интерпритация: R3
: n=3
Привед-е кв. формы к кв. виду 1)
|
26. Кривые второго порядка. Приведение прю 2-ого пор. к канонич. виду. Кривой 2-ого порядка на пл-ти наз. мн-во точек корд. кот.в нек-рой дек. сист. корд. удовл.усл-ю:Ax2+2Bxy+Cy2+Dx+Ey+F=0 (1) Теорема: Всякая линия 2-ого порядка на пл-ти представл. собой либо эллипс либо гиперболу, либо параболу, либо пару прямых (может быть совпадающих) либо точку, либо пуст мн-во Рассм ур-е (1) A
Квадратичная форма 2х переменных: x и y для матрицы.
Пусть
в ур-е (1) проведем замену переменных по формулам (2) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
27. Пов-ти 2ого порядка. Пов-тями 2ого пор. наз. такие мн-ва точек в пр-ве, координаты которых удовлетворяют уравнению вида Ax2+By2++Cz2+Dxy+Eyz+Fzx+ Gx +Hy +Kz+ L=0 (4) Например, ур-е x2+y2+z2=R2 определяет сферу радиуса R с центром в начале координат.
|
28.Псевдорешение системы лин. ур-й.
Теорема. Для любой
матрицы А размера (m×n)
существуют унитарные матрицы U
порядка m,
V
прядка n
такие, что
г
Из (5) следует, что
Такое представление матрицы А называют ее сингулярным разложением. С учетом (6) система (1) может быть записана в виде
или
Пусть сист. (7) принимает вид
|
Ии этот минимум равен
Если
k<n,
то
Обычно полагают,
называют нормальным
псевдорешением системы (9). Из первого
ур-я (8)
Если
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Введем векторы
и матрицу
Система (15) теперь записывается в виде
В больш. задач
m<n,
т.е. в сист. (16) число уравнений большн
числа неизвестных(система
переопределенная). Найти ее «точное»
решение малоперспективно. Поэтому
в-р
С учетом
вышеизложенного, если
Рассмотрим еще один вариант решения данной задачи.
Опр. Ф-и
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Возможны 3 случая.
1)
2)
3)
|
Сост унит. матр.
кв. ф.
Классификация кв. форм
|
24.Унитарные матрицы. Приведение к диагональному виду.
Опр. Кв. матр. Т над. унит. если Т*ТТ=I вещ. унит. матр. наз. ортогон. Т*=ТТ ТТТ=I Это означает, что Т- невырожденная. У матр. Т сущ обр. Т-1
Т*=Т-1
пусть
Умножим Т на Т
Унитарная матр. это кв. матр. у кот. столбцы явл. Ортонорм. Вект.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
29. МНК
Пусть результатом
эксперимента служит набор значений
неизвестной вообще говоря функции
Ставится задача:
найти функцию
Подставляя в (14)
x=xi,
i=1,2,...,n,
получим систему n
уравнений с m
неизвестными
|
Тогда система (7) принимает вид
Покажем, что
Действительно,
Система (9) с учетом
вида матрицы
При этом
Ясно, что минимум квадрата нормы невязки достигается при
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
попарно ортогональны,
т.е.
В этом случае
=
и, сл-но, решение системы (17) имеет вид
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||





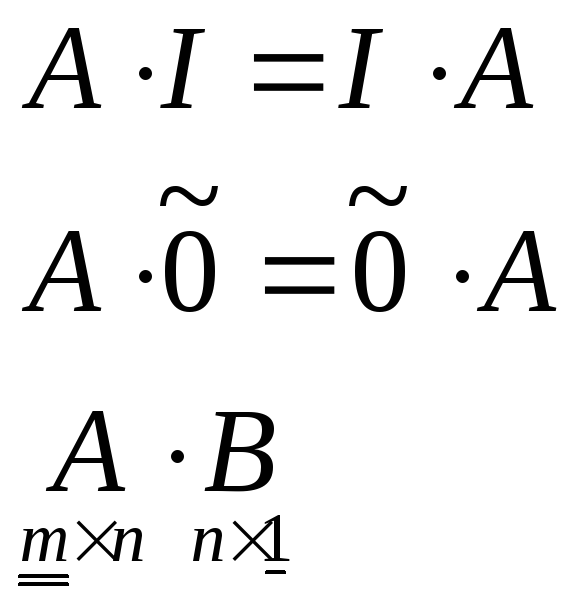

 удовлетворяет
условию, если в результате подстановки
их в уравнение, получим равное тождество.
удовлетворяет
условию, если в результате подстановки
их в уравнение, получим равное тождество.
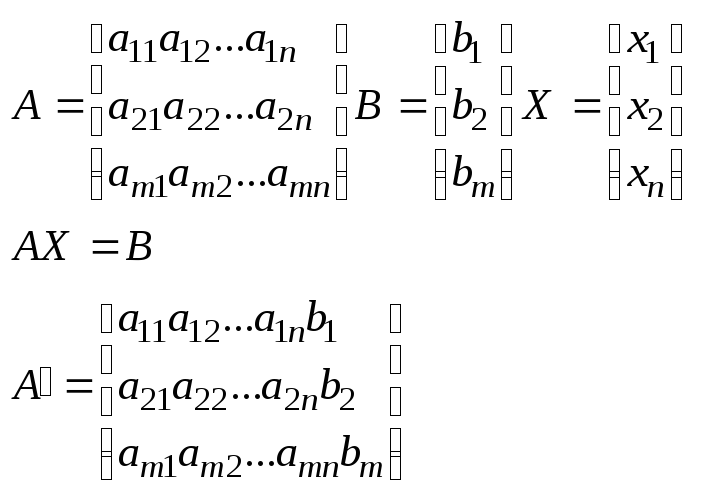

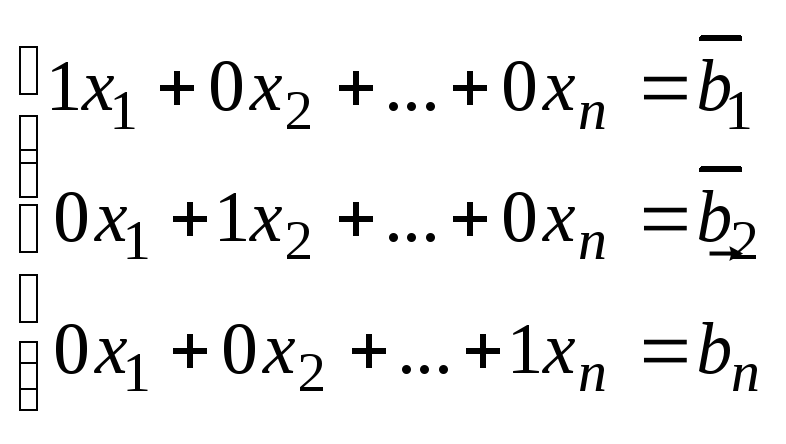
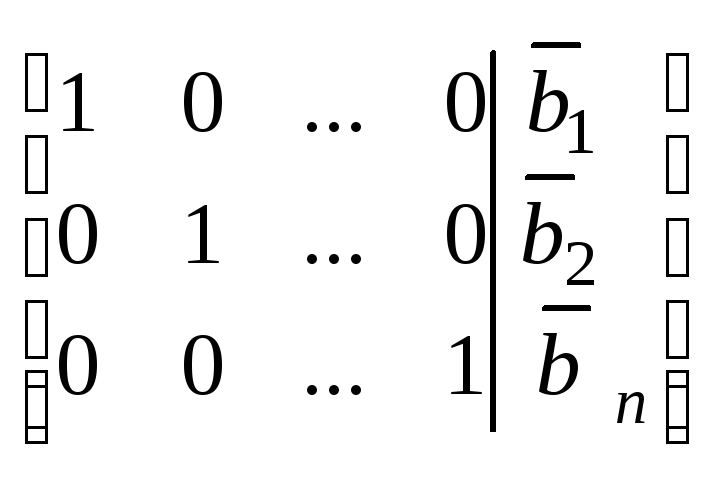 единственное
решение
единственное
решение
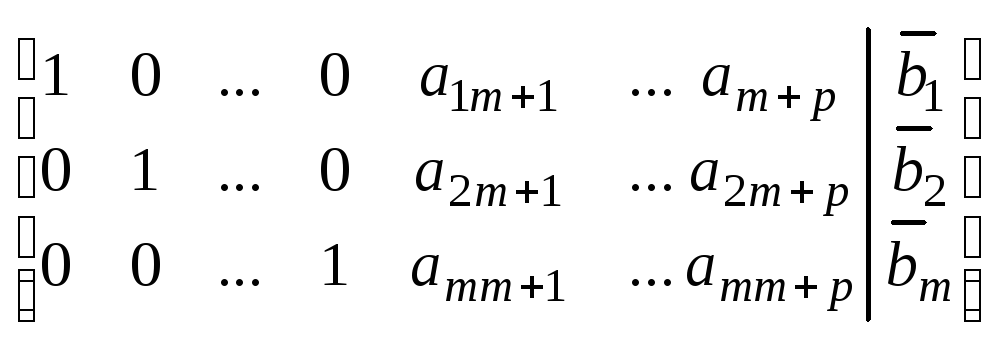
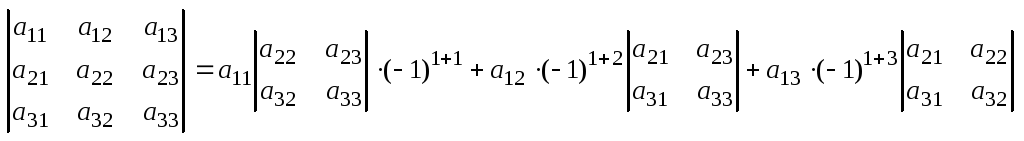
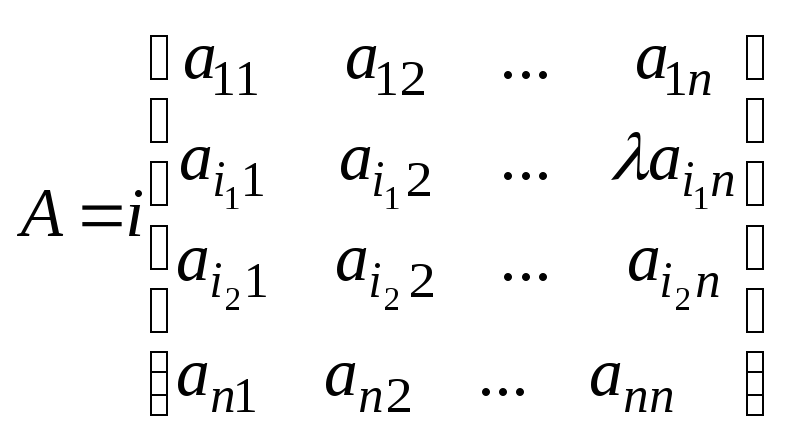
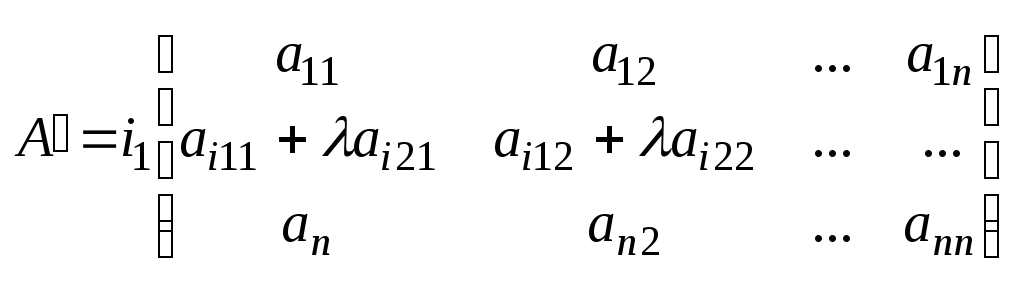





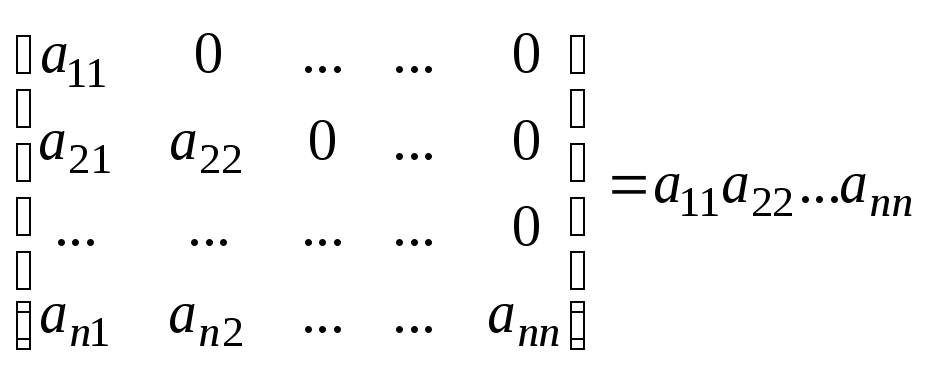
 1
≤ j
< i
≤ n
1
≤ j
< i
≤ n detA≠0
detA≠0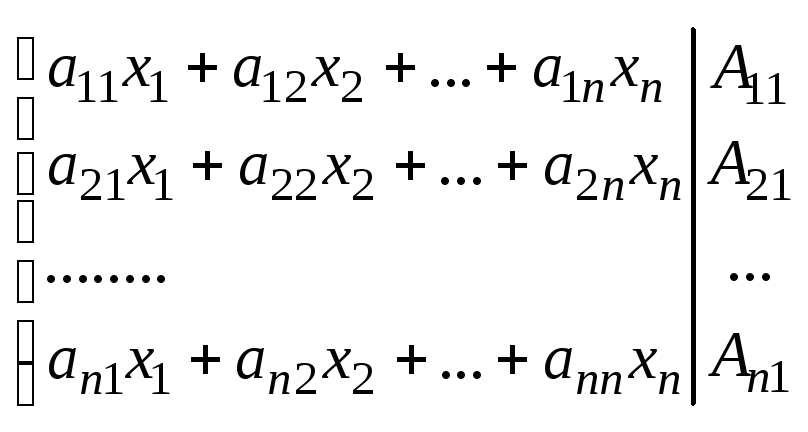
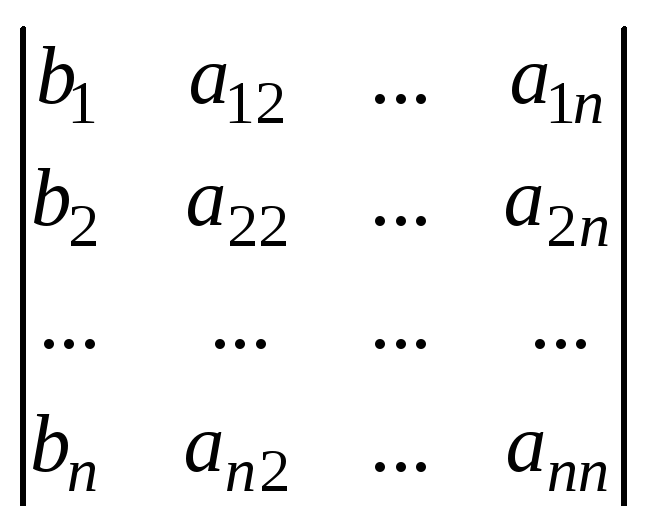
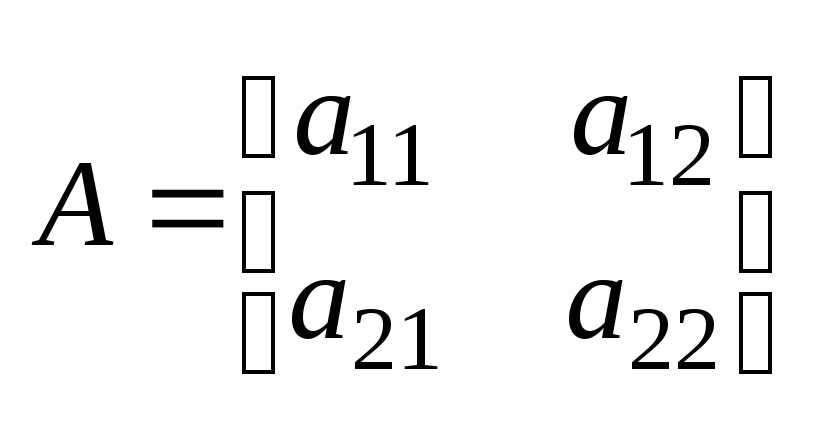
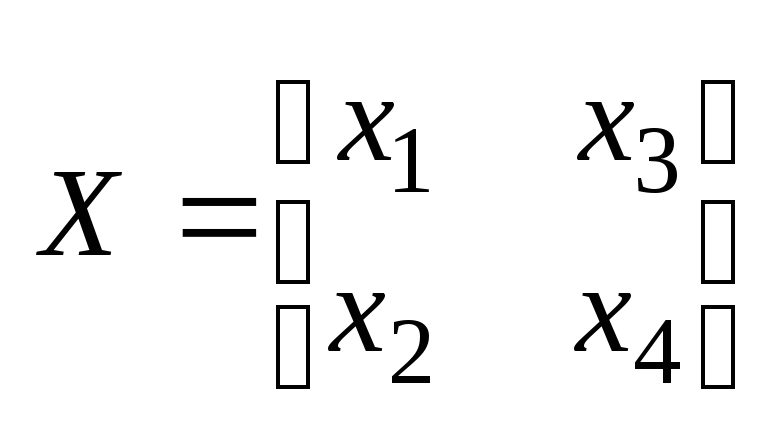



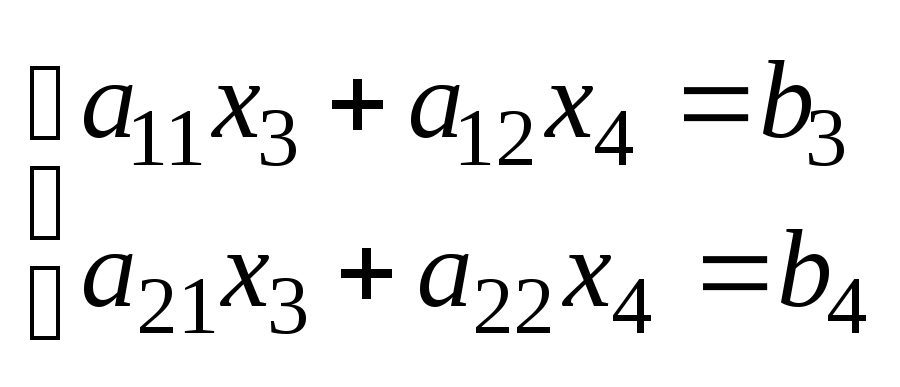
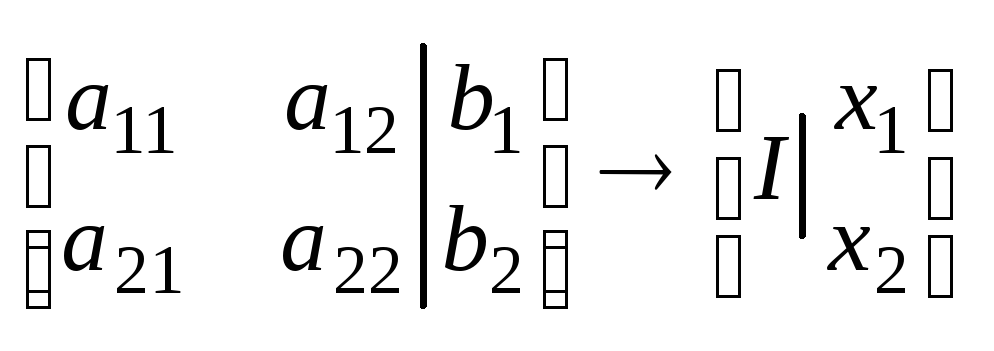

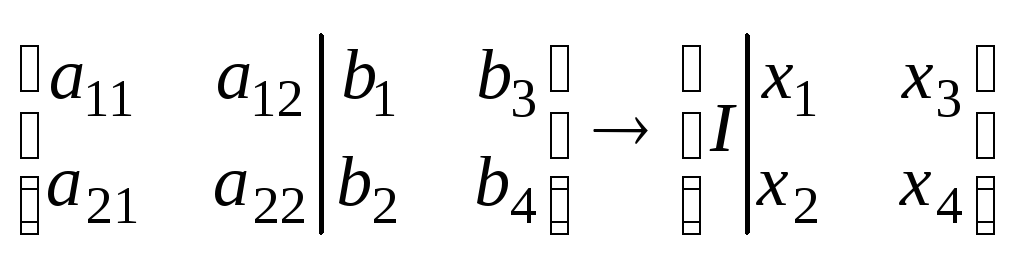
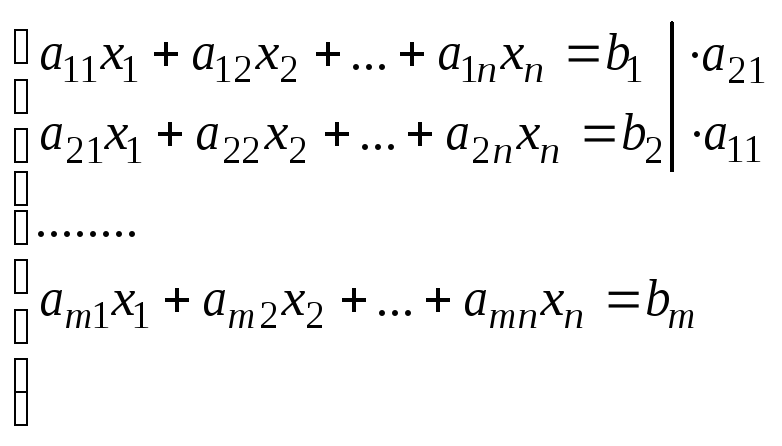



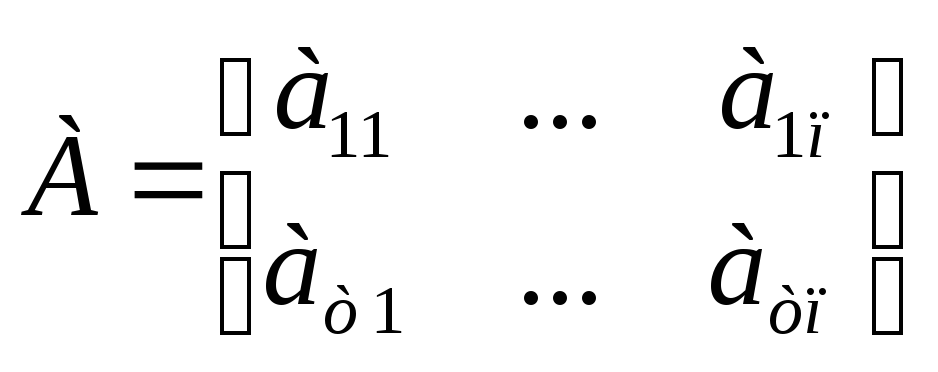

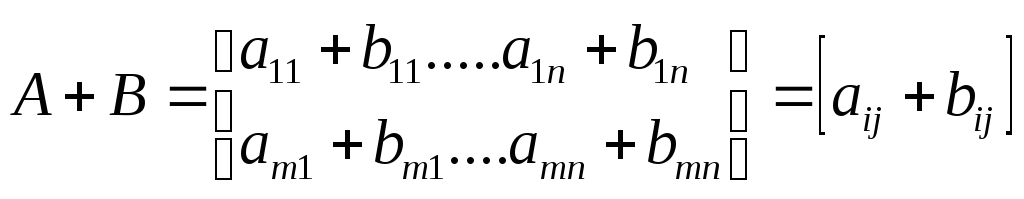
 A''=
A''=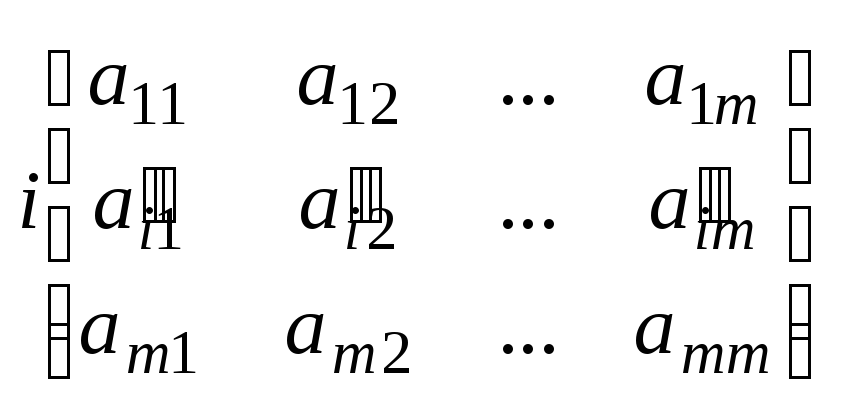
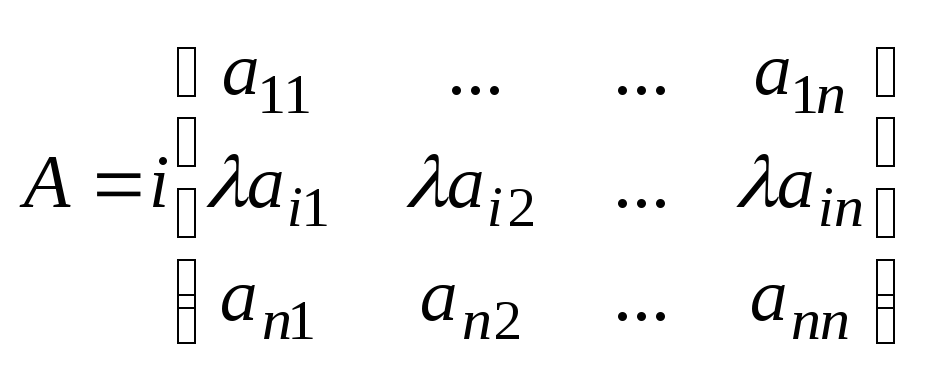
 r=3
A=
r=3
A=
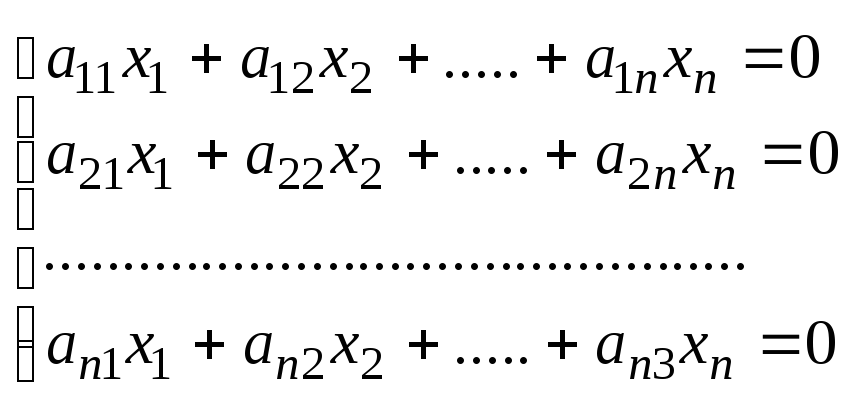
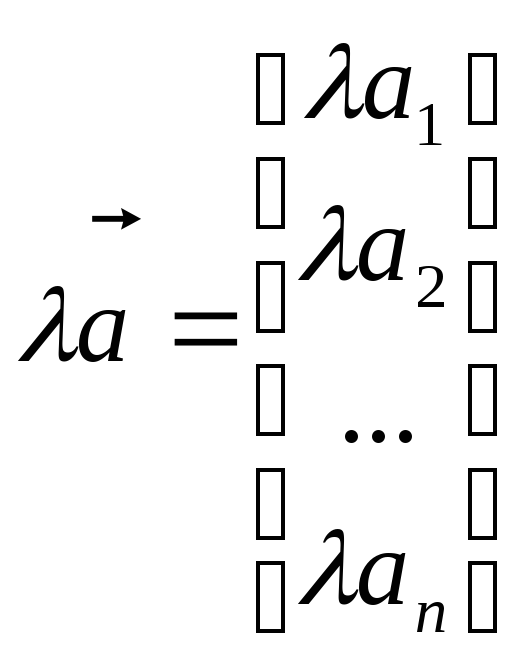
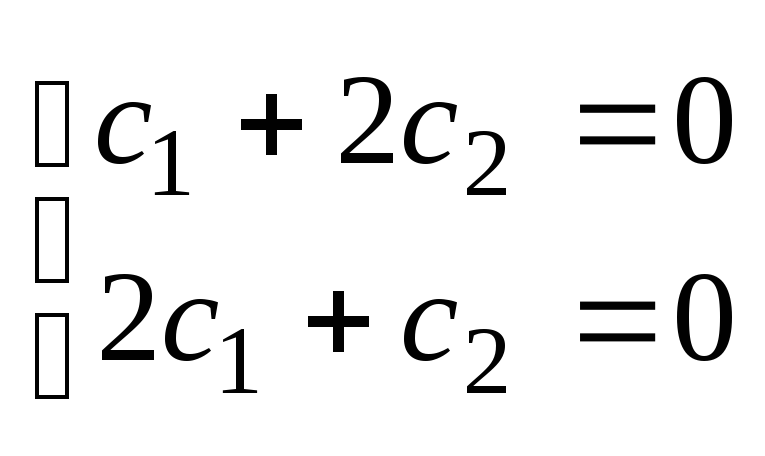

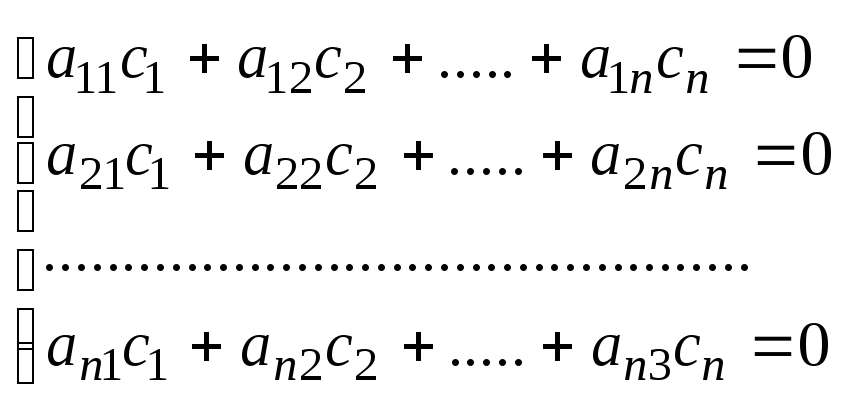



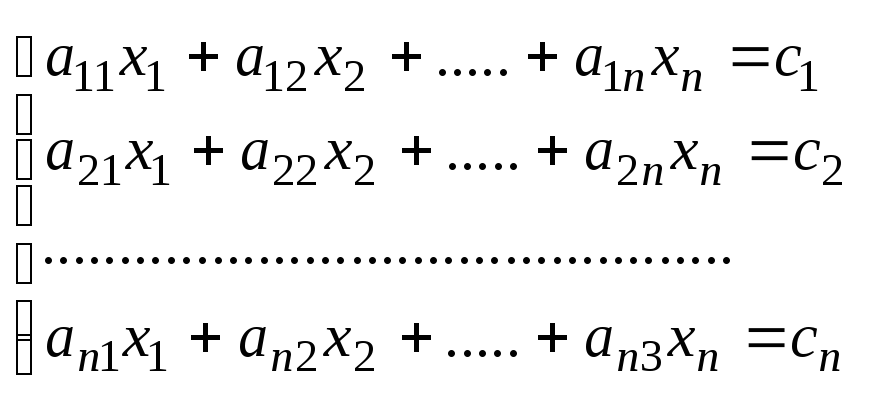
 координаты вектора
координаты вектора
 ≠0,
≠0,
 ти
векторы коллинеарны.
ти
векторы коллинеарны.
 наз.
n-
мерным вектором, a1,a2...
an-компоненты,
векторы с нулевыми компонентами наз.
нул. Мн-ва векторы у кот. эл. компл.
обозн. Сn,
Rn
векторы из пространства R
чисел.
наз.
n-
мерным вектором, a1,a2...
an-компоненты,
векторы с нулевыми компонентами наз.
нул. Мн-ва векторы у кот. эл. компл.
обозн. Сn,
Rn
векторы из пространства R
чисел.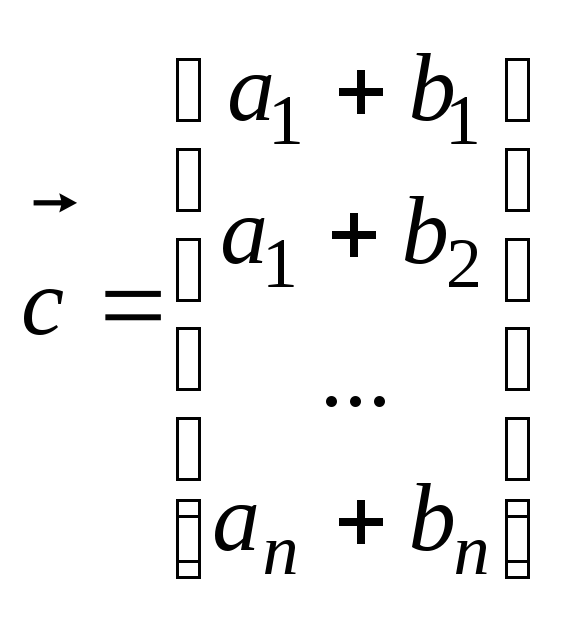
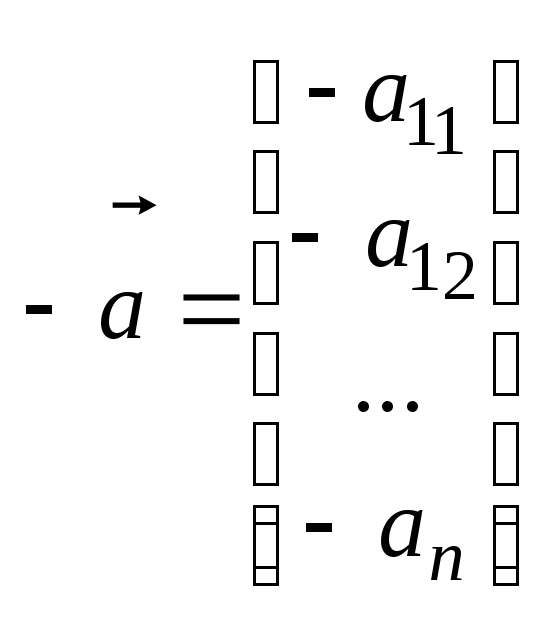

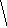

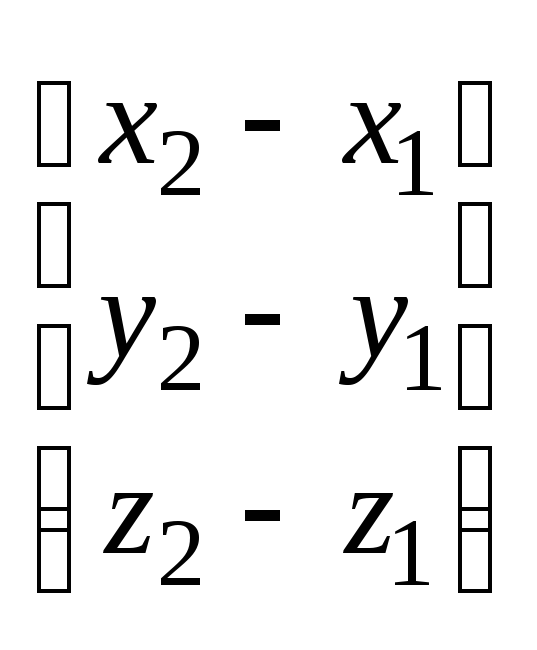
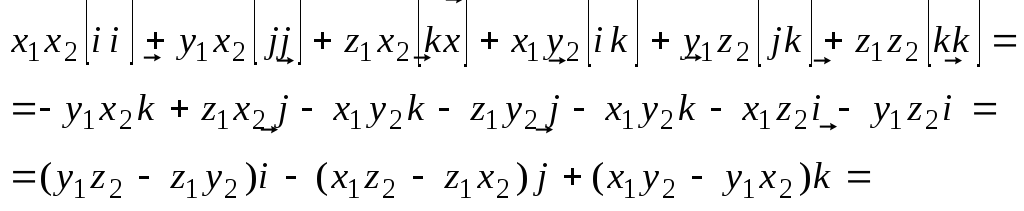



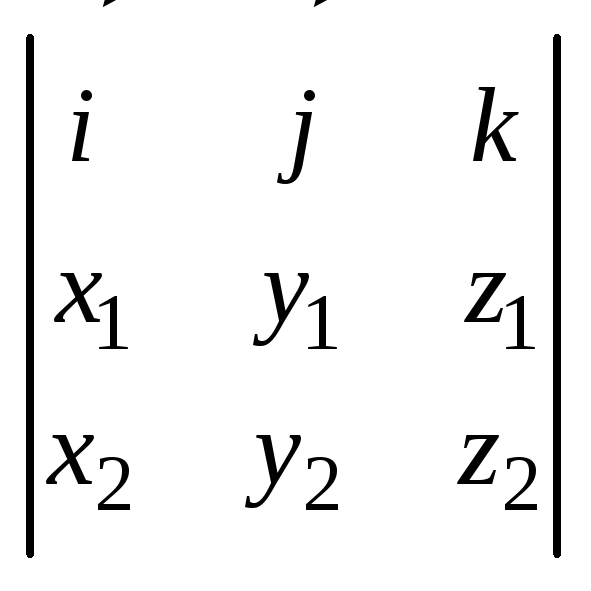
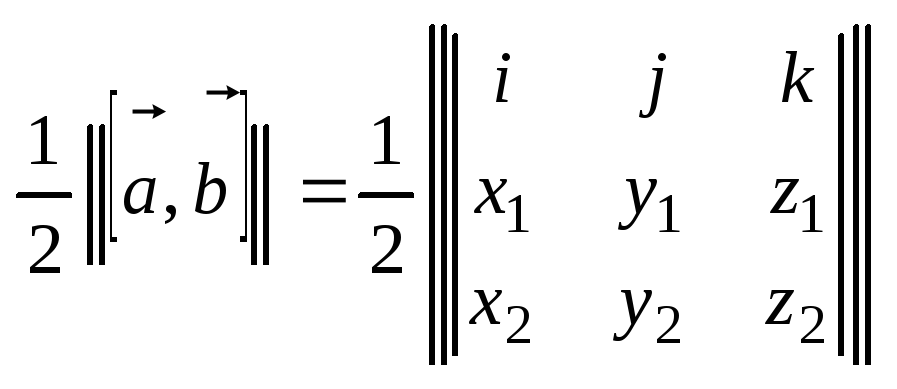



 .
.
 ×
×

 ×
× ×
×




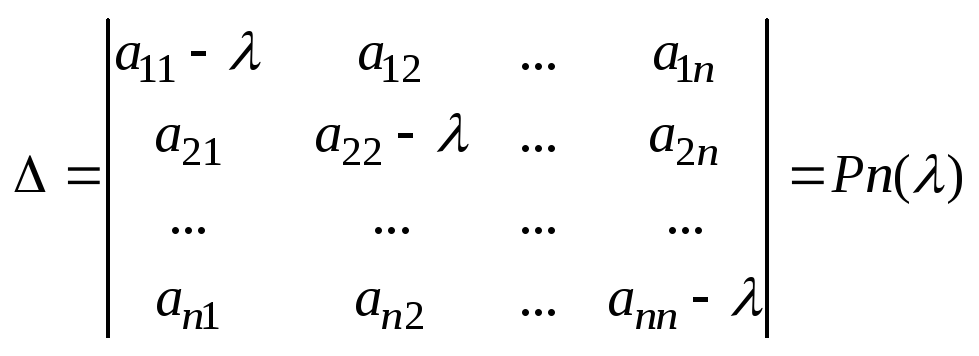

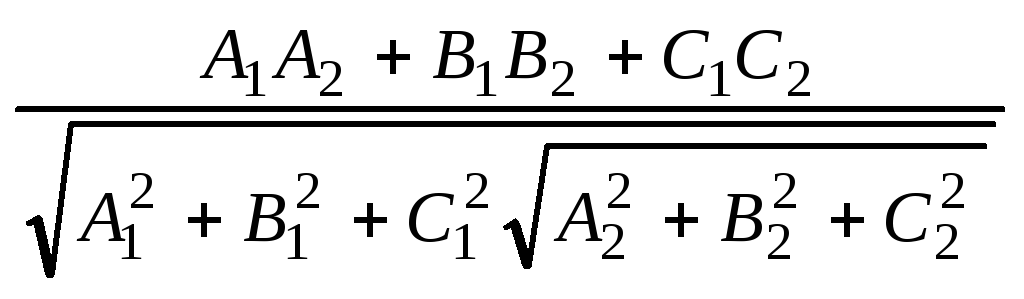
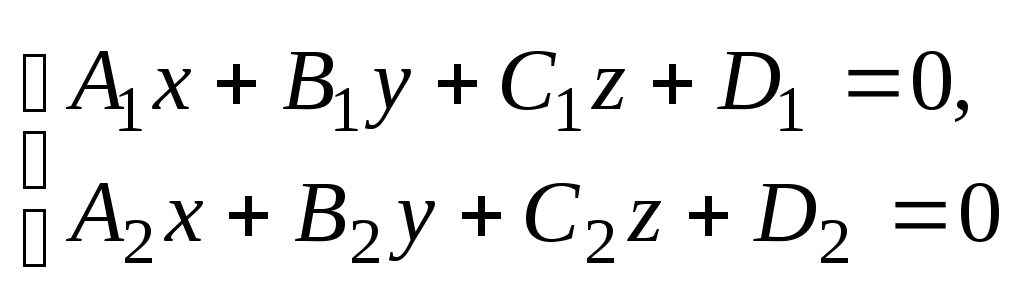 (3)
(3)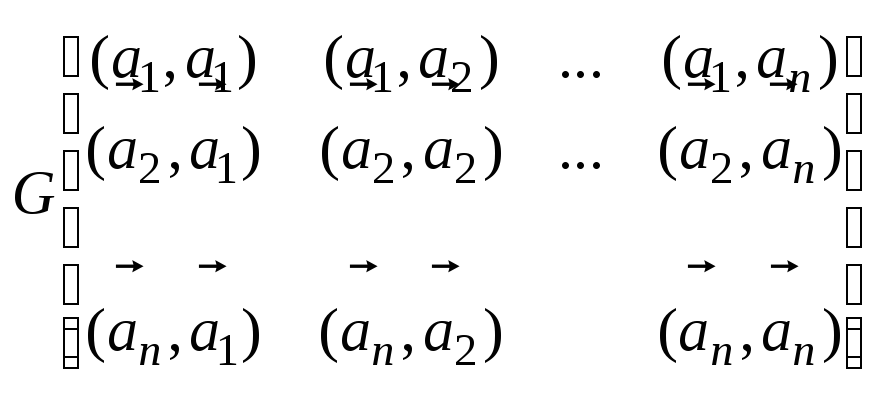
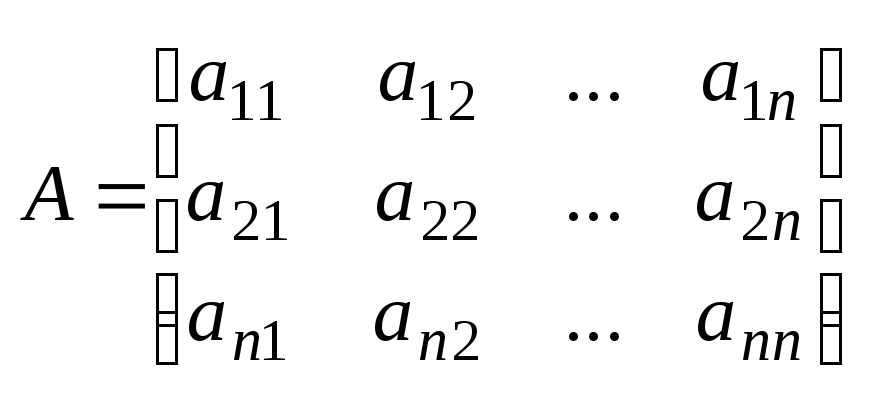
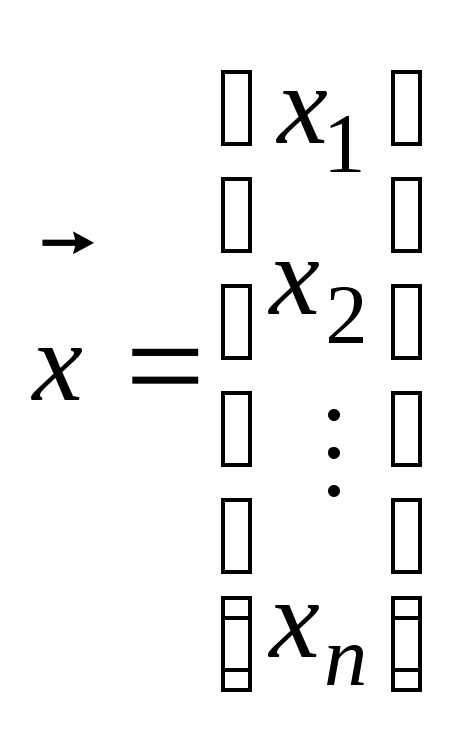

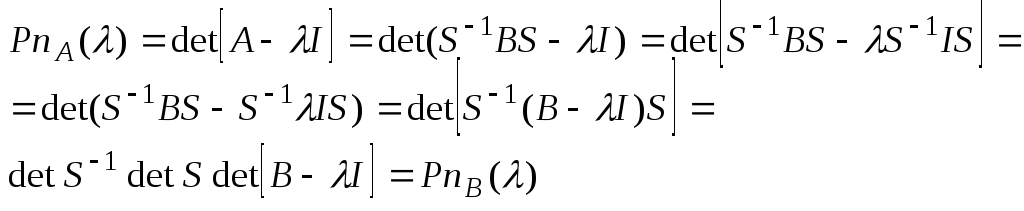

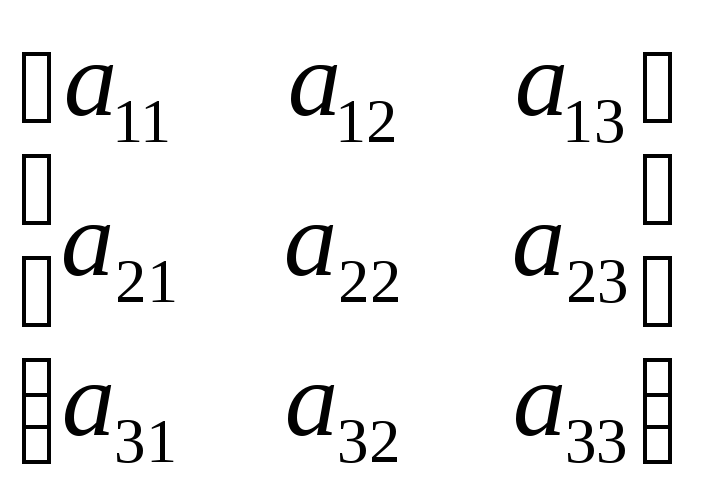

 x2+2Bxy+Cy2+Dx+Ey+F=0
x2+2Bxy+Cy2+Dx+Ey+F=0
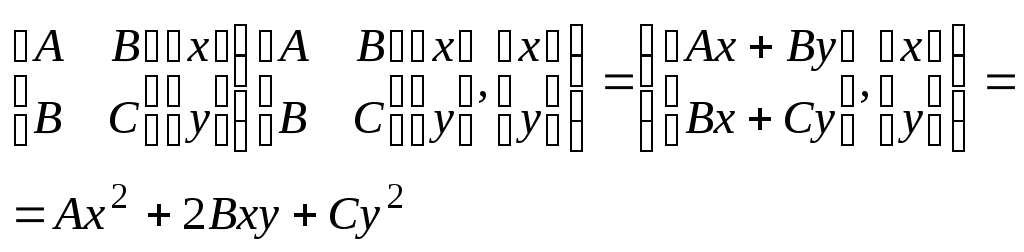
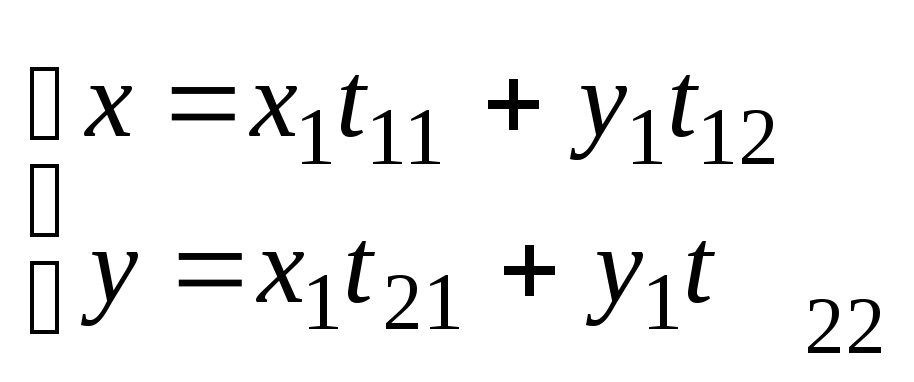 (2)
(2) де
де (5)
(5) ,
,

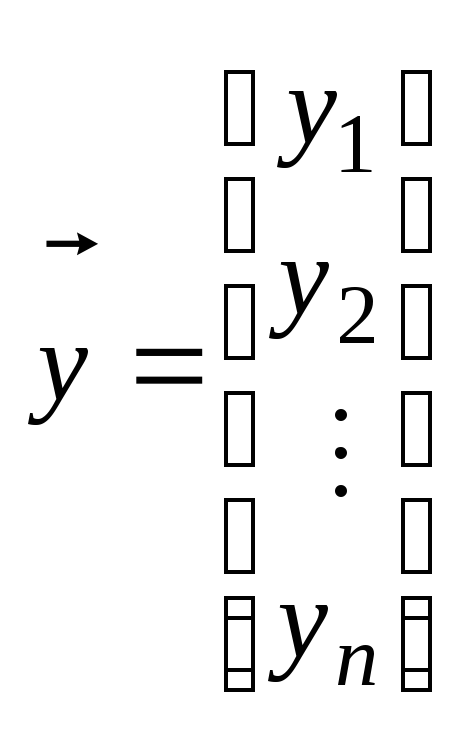
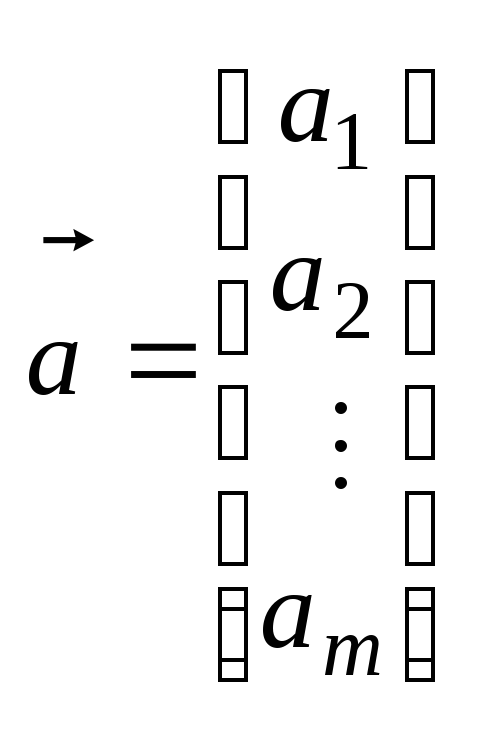
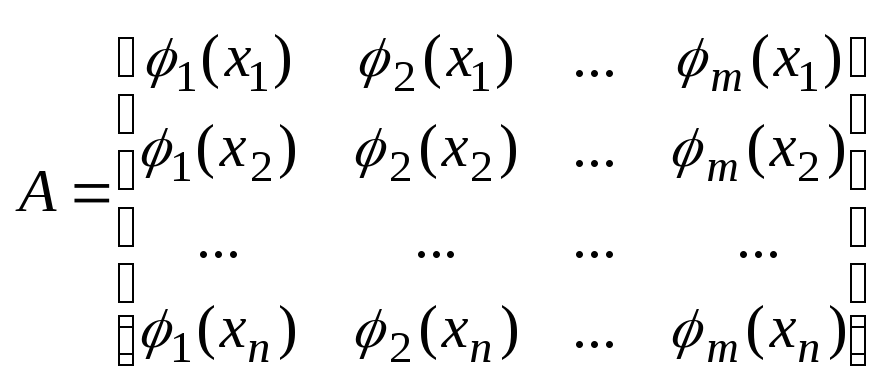

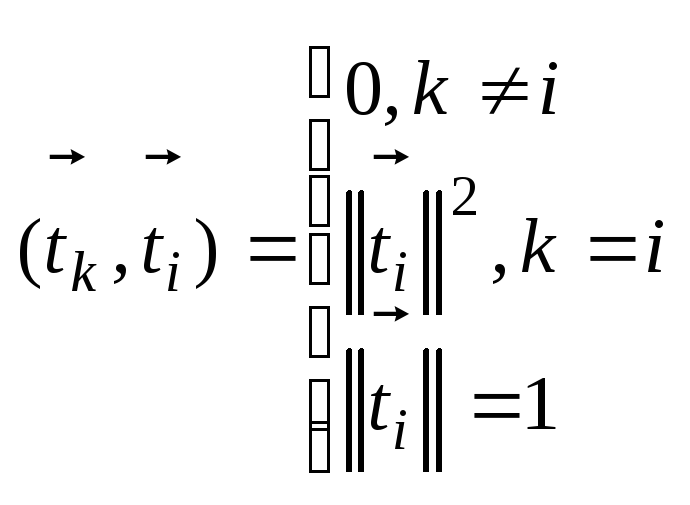

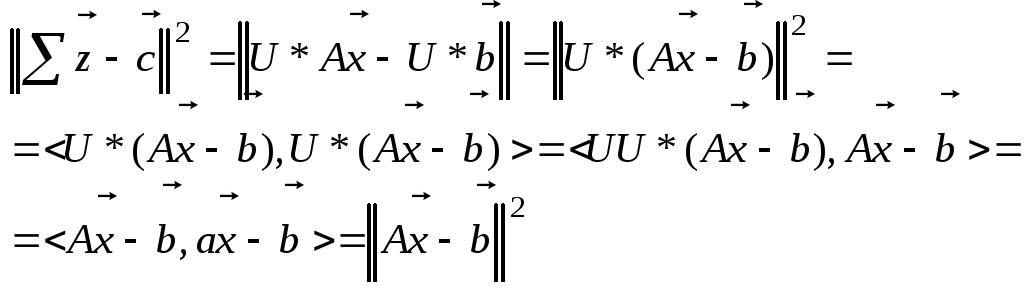
 (10)
(10)
 0
0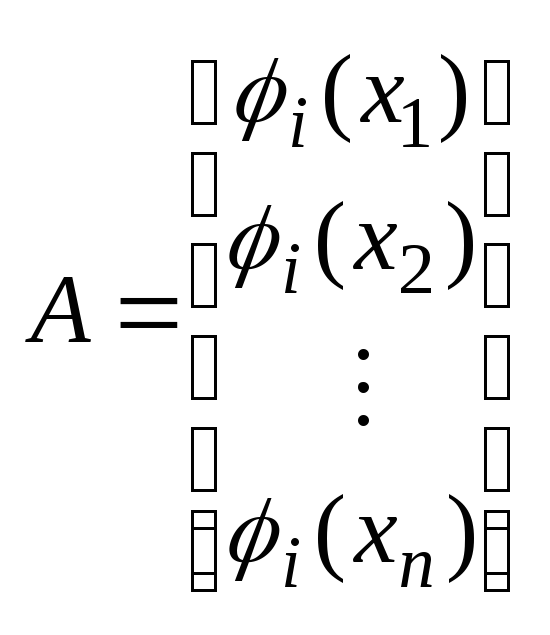 i=
1,2,///,n
i=
1,2,///,n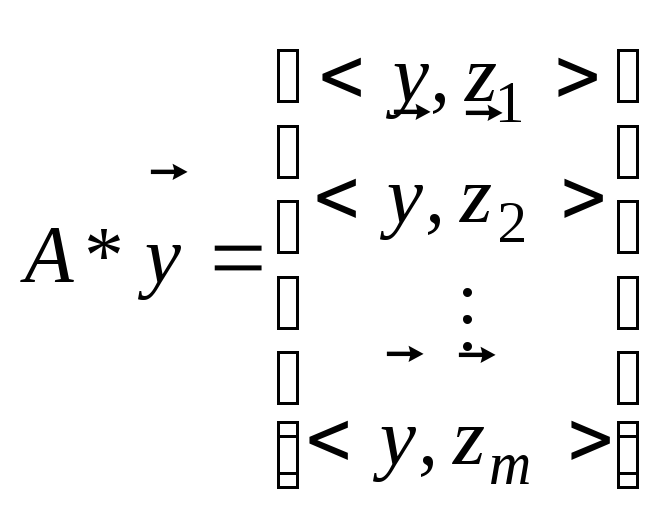
 i=1,2,..,n
i=1,2,..,n