2.Расчет структуры переменных электромагнитных полей в волноводе.

Общее задание.

Для заданного типа волны с начальной амплитудой поля =5кВ/см, распространяющейся в прямоугольном волноводе сечением получить аналитические выражения продольных и поперечных компонент полей в комплексной форме записи и для мгновенных значений. Для численных параметров задачи построить эпюры полей по осям X, Y, Z, а также картину распределения полей в плоскостях XY и XZ. Рассчитать заданные характеристики полей и построить их зависимости от частоты. Во всех случаях считать, что параметр μ=1.

Параметры задачи

Волна Е₁₁, ab=7.2x3.4мм; l=5.9мм, диэлектрическая проницаемость e=1. Рассчитать k_p и Z_э.

Решение

Эскиз исследуемого волновода приведен на рисунке 2.1. Оси координат расположены в соответствии с этим рисунком.

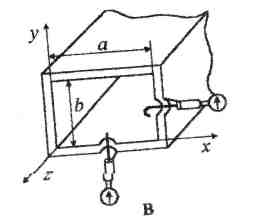
Рисунок 2.1

Полость волновода заполнена диэлектриком, электрическая проницаемость которого e. Длина волновода в направлении оси z не ограничена. Процесс распространения электромагнитных волн в полости прямоугольного волновода рассматриваем, полагая, что стенки волновода выполнены из сверхпроводящего материала (g=¥). При этом условии напряженность электрического поля на стенках волновода будет равна нулю (плотность тока на стенках волновода d=gE есть величина конечная, поэтому при g®¥, E®0).

Электромагнитное поле в волноводе описывается волновым уравнением:

(2.1)

где – круговая частота, – абсолютные электрическая и магнитная проницаемости.

Для заданного типа волны выполняется следующее условие:

Распространяющиеся в волноводе электромагнитные волны являются волнами, бегущими вдоль оси волновода (оси z) и стоячими в двух остальных направлениях.

В соответствии с (2.1) волновые уравнения для продольных компонент поля будет иметь вид:

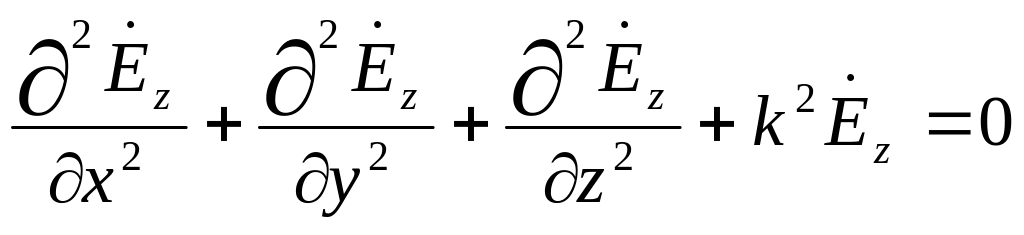(2.2)

где - волновое число; - длина волны в неограниченном пространстве; - круговая частота; и - соответственно абсолютные и относительная проницаемости.

Упростим уравнение (2.2) путём подстановки решения вида:

, (2.3)

где kp= - продольный коэффициент распространения в волноводе; – длина волны в волноводе. Сокращая на множитель , имеем:

(2.4)

Для решения уравнения (2.4) воспользуемся методом разделения переменных. С этой целью положим:

(2.5)

и подставим в (2.4):

(2.6)

Разделим (2.5) на XY и получим:

Сумма двух независимых функций в левой части уравнения может равняться постоянному числу только в том случае, если каждая из этих функций есть постоянное число. Переходя от частных производных к обыкновенным, имеем:

, (2.7)

Здесь через kx и ky обозначены постоянные разделения (поперечные волновые числа), удовлетворяющие равенства:

,

.

Проверим:

из условий ассиметрии =0, тогда X=

(аналогично проводиться операция проверки для Y)

Исходя из соотношения (2.5), имеем выражение для амплитуды (волновой множитель опускается) продольной составляющей электрического поля:

, (2.8)

где -начальная комплексная амплитуда; kx, ky, , - постоянные интегрирования.

Для нахождения поперечных компонент поля воспользуемся уравнением Максвелла в проекциях на оси координат при условии Hz=0:

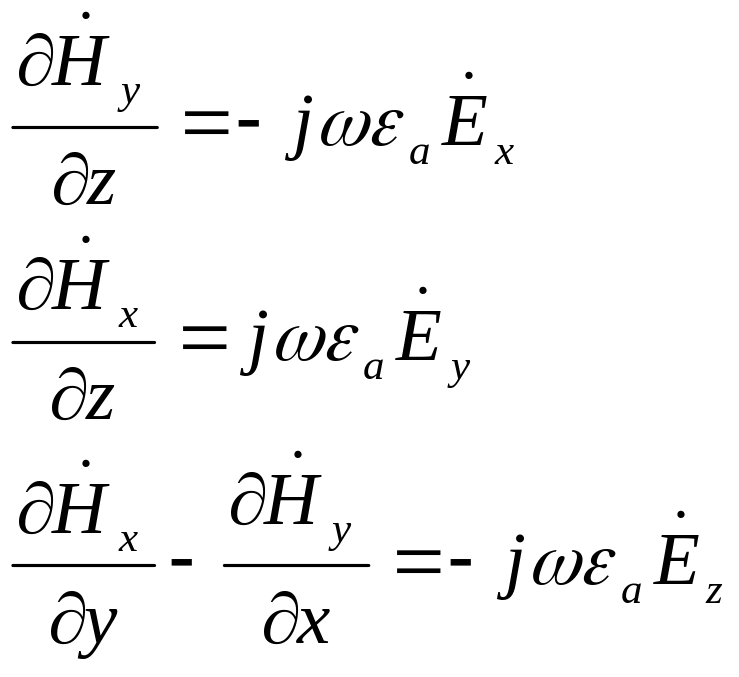
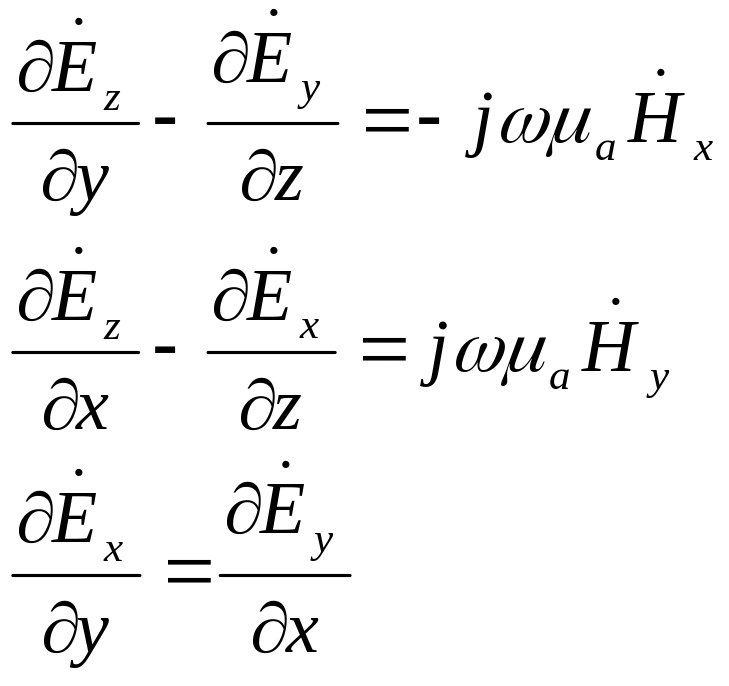(2.9)

Поскольку характер изменения полей по оси z задаётся выражением (2.2), то в (2.8) примем, что =-jkp . Рассматривая затем первое и пятое уравнения как систему для и , а второе и четвёртое - и , решим их.

Первая система:

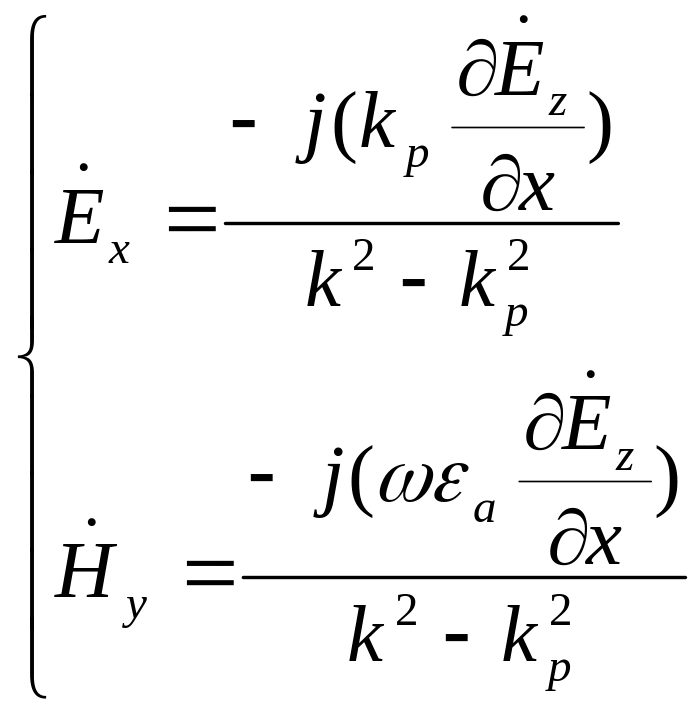
Вторая система:

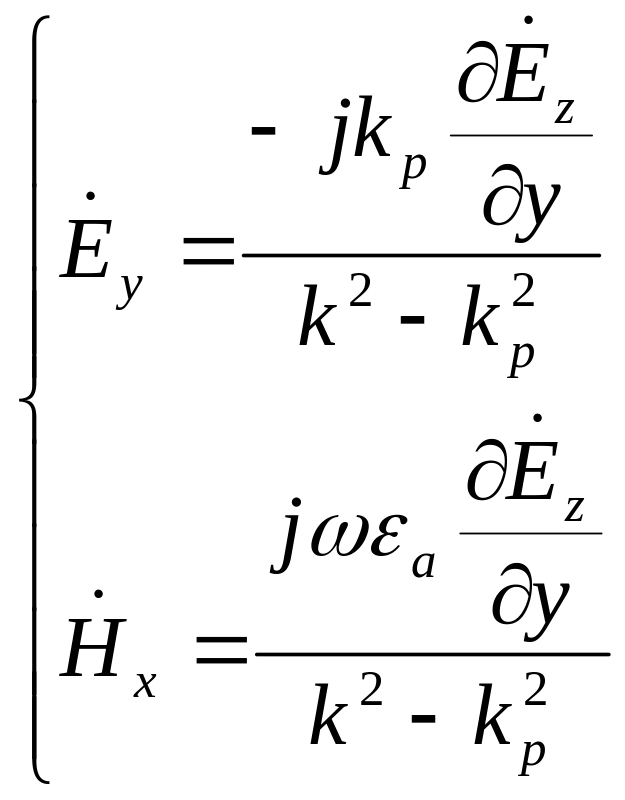
Мы получили следующие выражения для поперечных составляющих полей через продольные:

(2.10)

Подставляя в (2.10) значение , получаем выражения для поперечных составляющих поля:

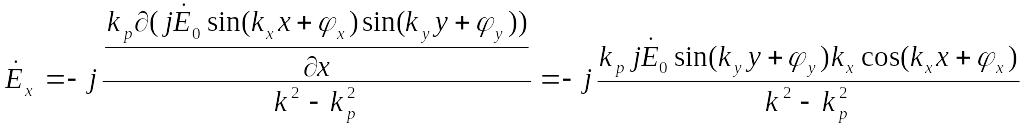
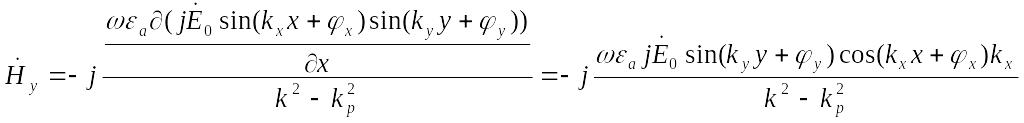
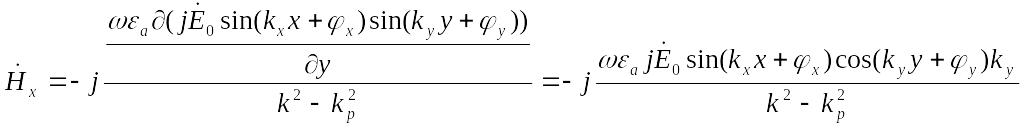
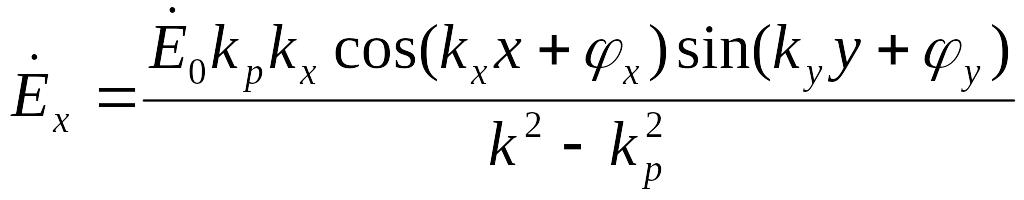
(2.11)

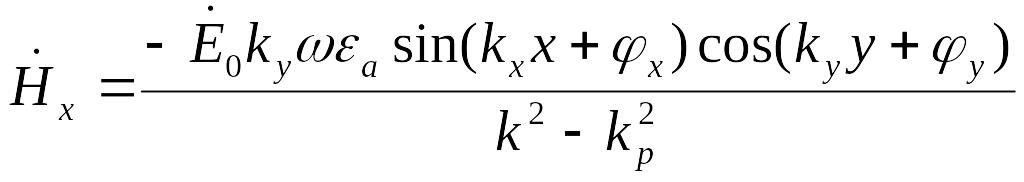
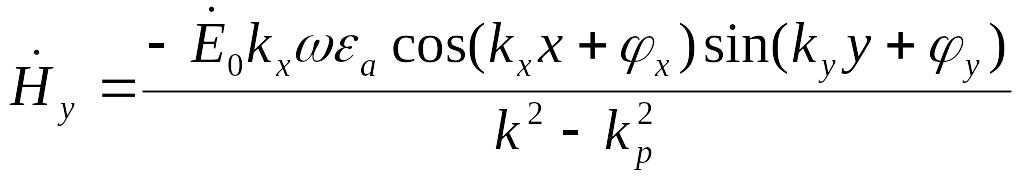
Для упрощения будем считать, что потери в стенках волновода и в заполняющем его диэлектрике отсутствуют. Это даёт возможность проще сформулировать граничные условия: на стенках волновода отсутствует касательная составляющая электрического поля ( при x=0 и x=a, при y=0 и y=b).

Так как:

,

а при x=0, x=a при y=0 и y=b, то из 4-го и 5-го уравнений в (2.9) найдём:

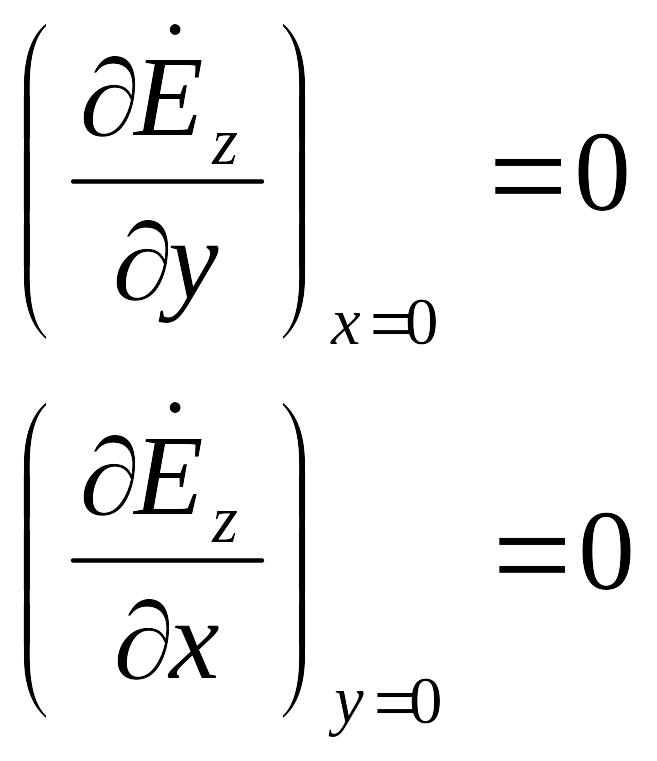
Подставив в эти уравнения (2.8), найдём и , а также и , где m, n – целые числа; m равно числу полуволн электромагнитной волны, которые разместятся по ширине волновода; n показывает, сколько полуволн разместится по высоте волновода. Окончательные выражения для составляющих поля после подстановки постоянных принимают вид:

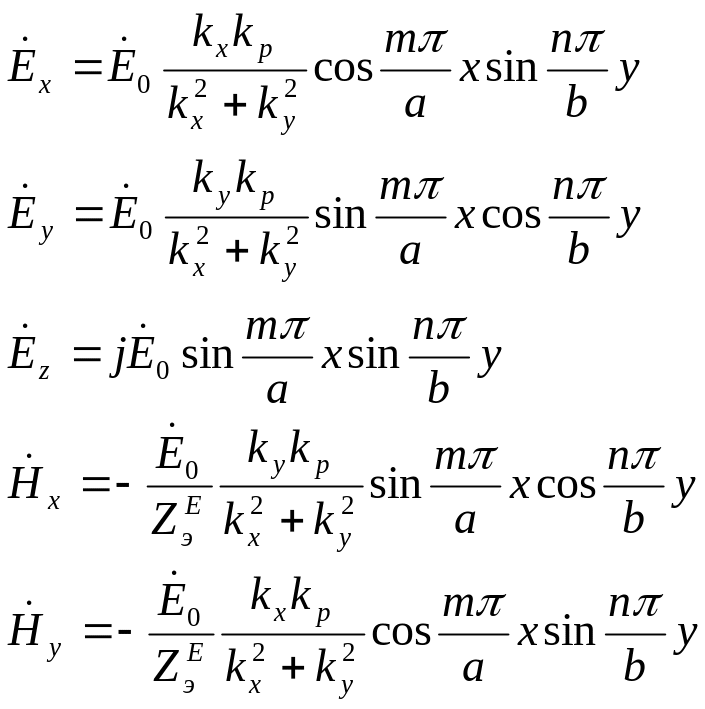(2.12)

где - эквивалентное сопротивление волновода для Е-волны; - волновое сопротивление неограниченной среды; fкр – критическая частота.

Аналитические выражения для составляющих поля волны Е11 получаем из (2.12) при m=1; n=1:

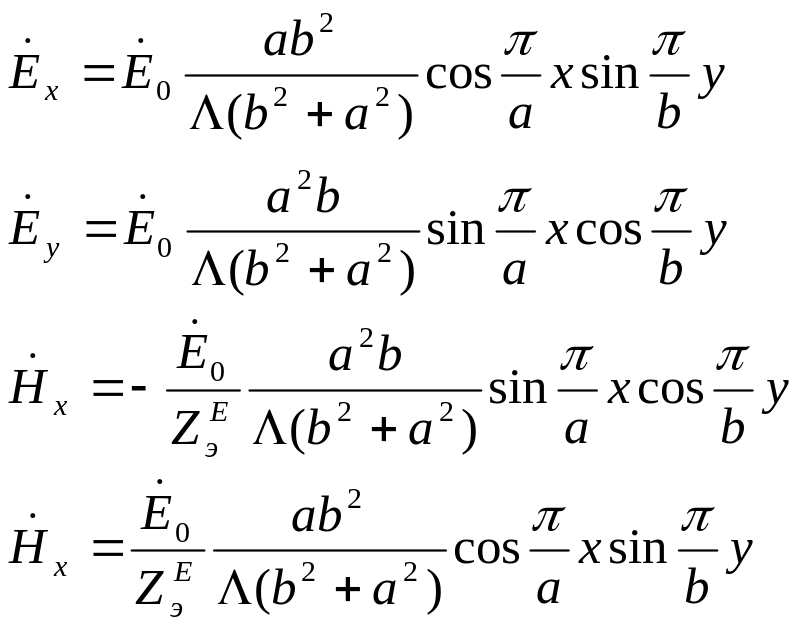(2.13)

Для восстановления действительных значений необходимо компоненты полей помножить на опущенный ранее волновой множитель , перейти по формуле Эйлера к тригонометрической форме записи и взять действительную часть полученного выражения. Продемонстрируем данную операцию на примере Ех компоненты:

(2.14)

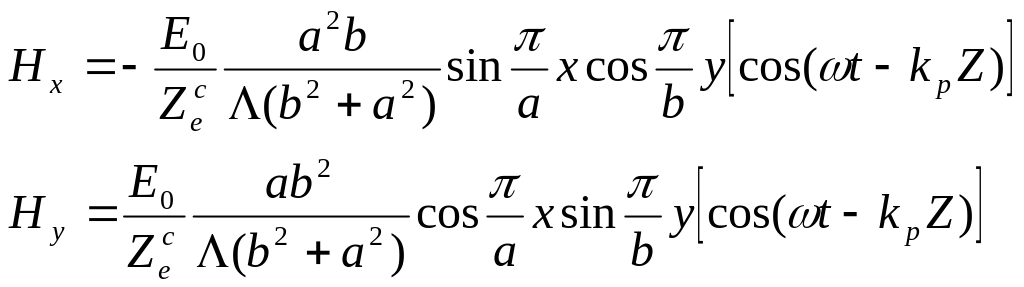
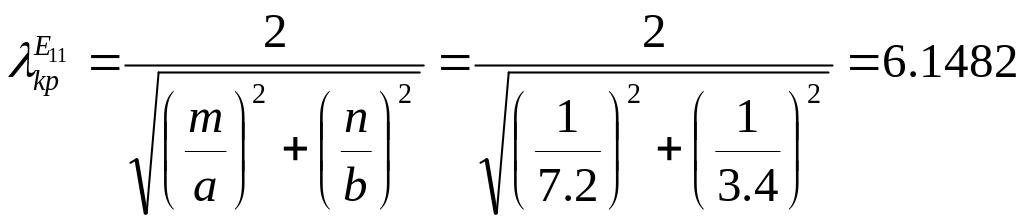
Входящие в (2.14) значения Zэ, , и kp равны:

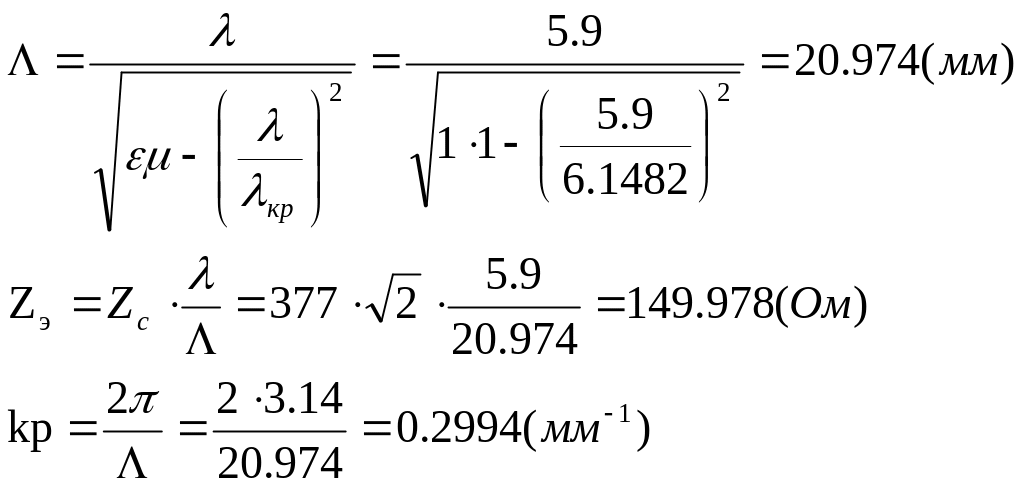
Выводы

1. При выполнении курсовой работы были приобретены навыки по расчету структуры стационарных потенциальных полей и переменных электромагнитных полей в направляющих системах, а также закреплены навыки основ программирования и работы на персональных компьютерах.

В соответствии с заданием на курсовую работу были выведены выражения для потенциала и напряженности полей, рассчитаны ( с помощью ЭВМ) семейство эквипотенциальных линий для проводящий цилиндр в магнитной среде.

2. В случае переменного электромагнитного поля в прямоугольном волноводе получены аналитические выражения для электрических и магнитных компонент поля, построены их распределения в поперечном и продольном сечениях. В поперечных сечениях волновода вдоль осей x, y образуются стоячие волны в результате наложения многократных отражений от стенок волновода электромагнитного поля. Длина волны в волноводе больше длины волны в свободном пространстве. При таком условии возможно нормальное распространение электромагнитных волн (без затухания).