Методика расчета

1.Расчет структуры осесимметричных стационарных электромагнитных полей.

Общее задание.

Осесимметричное тело радиуса R находится в однородном внешнем электрическом поле Е₀, перпендикулярном к его оси. Заданы характеристики окружающей среды. Получить аналитические выражения для потенциалов и и полей Е_i и Е_e, соответственно внутри и вне тела. Для заданных численных значений параметров задачи построить семейство эквипотенциальных линий (10 линий) в плоскости, перпендикулярной оси симметрии тела.

Найти вектор электрической индукции D в точке М.

Параметры задачи

Бесконечный диэлектрический цилиндр в диэлектрической среде,

R=3см=0,03м, Е₀=20 , =2, =8

К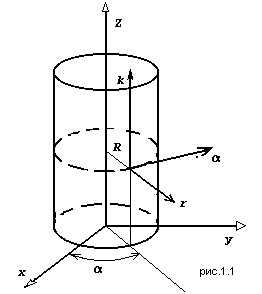 оординаты точки M: r=2см=0,02м, =45

Решение

Решение проводится в цилиндрических координатах, связанных с центром основания цилиндра, r — радиус-вектор точки наблюдения, ось x направлена вдоль приложенного магнитного поля (рис. 1.1).

Потенциал поля не зависит от координаты z. Учитывая это, запишем уравнение Лапласа:

(1.1)

Внутри и вне цилиндра сторонних зарядов нет, поэтому следует решать уравнение Лапласа с соответствующими граничными условиями на поверхности r=R.

Решим уравнение (1.1) методом разделения переменных, в соответствии с которым решение  будем искать в виде произведения двух функций, каждая из которых зависит только от одной координаты:

(1.2)

После подстановки выражения (1.2) в (1.1) получается

Умножая на получим:

Это равенство не должно нарушаться, если одну из независимых переменных r или  произвольно менять, а другой придать произвольное, но постоянное значение:

(1.3)

(1.4)

Этим самым решение уравнения (1.1) с частными производными сведено к решению обыкновенных дифференциальных уравнений.

Прежде всего надо найти частные решения уравнений (1.3) и (1.4) для p=0. Обозначим их M0 и N0, и в результате получим:

Т. к. потенциал является четной функцией относительно , т. е.: то необходимо принять

Если взять, согласно равенству (1.2), произведение функций и и изменить обозначение постоянных, то можно получить частное решение уравнения Лапласа в виде:

(1.5)

Пусть теперь постоянная разделения p в уравнениях (1.3) и (1.4) отлична от нуля.

Для решения уравнения (1.3) применим подстановку Эйлера Первая и вторая производные соответственно будут равны:

Подставим производные в уравнение

или (1.6)

Значение p определим при интегрировании уравнения (1.4):

(1.6`)

Решение его можно записать в виде .

Так как, если записать уравнения (волновое) гармонического осциллятора, то:

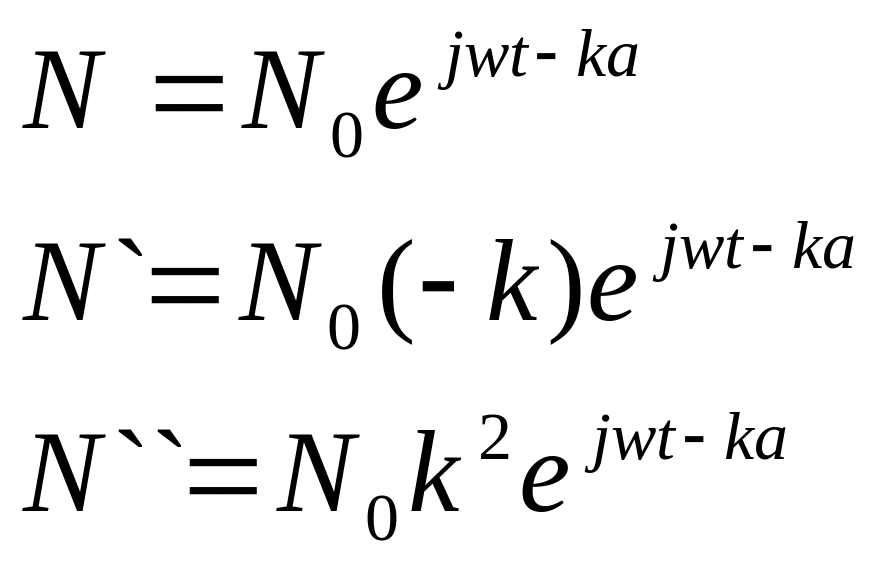
подставим их в уравнение (1.6`) :

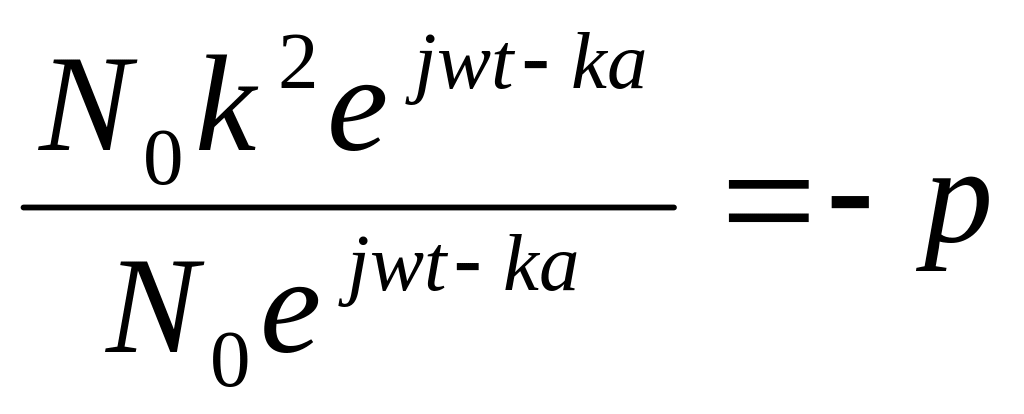отсюда к²=-р , (характер. ур.)

отсюда следует к=i.

N=N₀(cos(a)-jsin(a))=N₀cos(a)-jN₀sin(a)

Отбрасуем -jN₀sin(a) так как из условии азимутальной симметрии у нас по (а) парная функция.

N= N₀cos(a)

Убедимся в этом путем подстановки и одновременно найдем значение p:

Следовательно, p = 1.

После нахождения числа p подставим его в (1.6) и найдем n: и

Таким образом, совместное решение уравнений (1.3) и (1.4) при p, не равном нулю, дает следующее выражение для

(1.7)

Полное решение:

(1.8)

Найдем значения С₁, С₂, С₃ и С₄. Величины, служащие для описания поля внутри цилиндра, обозначим с индексом i, а величины, с помощью которых записывается потенциал во внешней по отношению к цилиндру области, - с индексом e. Таким образом, для внутренней области:

(1.9)

Для внешней области:

(1.10)

Надо найти 8 постоянных интегрирования. Потенциал на бесконечности в этом случае:

Сопоставим последнее выражение с (1.10):

откуда

Из граничных условий и , при находим, что

, .

Тогда внутри цилиндра ,

потенциал

а внутри цилиндра, то

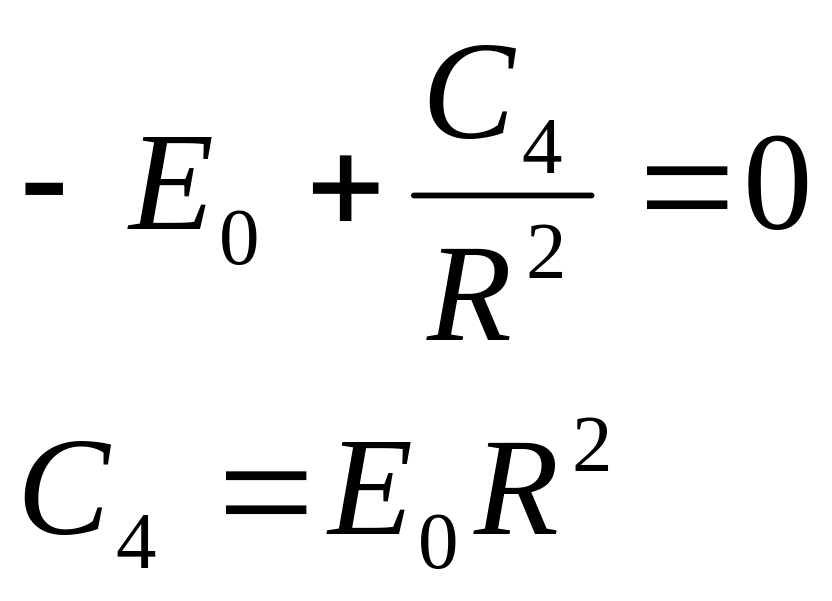
Тогда потенциал вне цилиндра будет равен

Е_i=0.

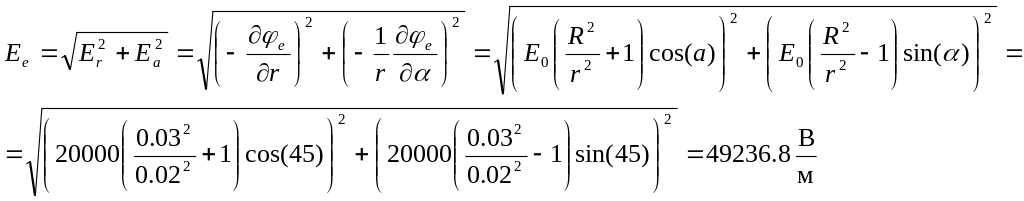
Е_e= 49236,8 В/м

Вектор электрической индукции в точке М (r=0,02м, =45):

D=