Основные понятия математической статистики

vk.com/club152685050 | vk.com/id446425943

15.Статистические методы. Вычисление m-мерного интеграла по методу Монте-Карло. Условия, при которых возможен поиск решения. Зависимость абсолютной погрешности от количества испытаний.

Предположим, требуется вычислить определённый интеграл

Рассмотрим случайную величину 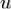, равномерно распределённую на отрезке интегрирования 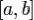. Тогда 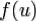так же будет случайной величиной, причём её математическое ожидание выражается как

,

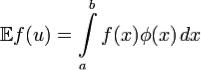где 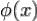— плотность распределения случайной величины 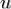, равная 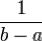на участке .

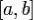Таким образом, искомый интеграл выражается как

.

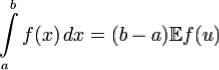Но матожидание случайной величины можно легко оценить, смоделировав эту случайную величину и посчитав выборочное среднее.

Итак, бросаем 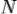точек, равномерно распределённых на 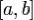, для каждой точки 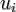вычисляем 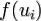. Затем вычисляем выборочное среднее:

.

В итоге получаем оценку интеграла:

Точность оценки зависит только от количества точек .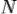

Этот метод имеет и геометрическую интерпретацию. Мы забрасываем область интегрирования случайными точками, на каждой из которых строим «столбик»,

определяя его ширину как 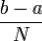, и суммируем их площади.

Для малого числа измерений интегрируемой функции производительность МонтеКарло интегрирования гораздо ниже, чем производительность детерминированных методов. В случаях, когда функция задана неявно, а необходимо определить область, заданную в виде сложных неравенств, этот метод может оказаться более эффективным.

vk.com/club152685050 | vk.com/id446425943

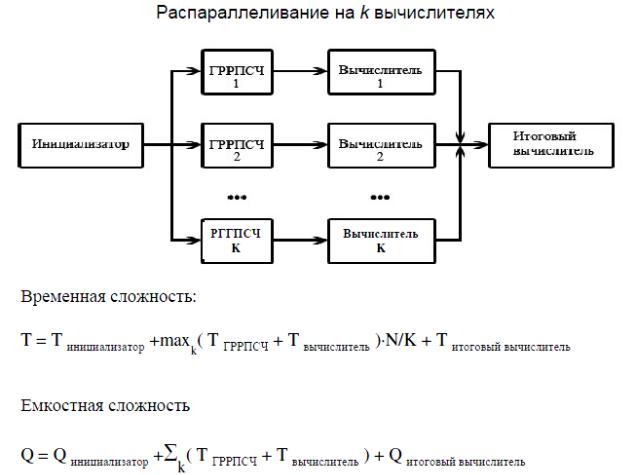
16. Статистические методы. Вычисление m-мерного интеграла по методу Монте-Карло. Распараллеливание вычислений: инициализация,

генерирование равномерно распределенных чисел, вычисления промежуточные и итоговые.

Типичное применение – интегрирование по методу Монте-Карло.

где x(i) - равномерно распределённое случайное число ( a, b ).

Для вычисления интеграла от одной переменной существуют детерминированные методы (например, метод аппроксимации). Метод Монте-Карло эффективен для вычисления определенных интегралов для функции от многих переменных m.

vk.com/club152685050 | vk.com/id446425943

vk.com/club152685050 | vk.com/id446425943

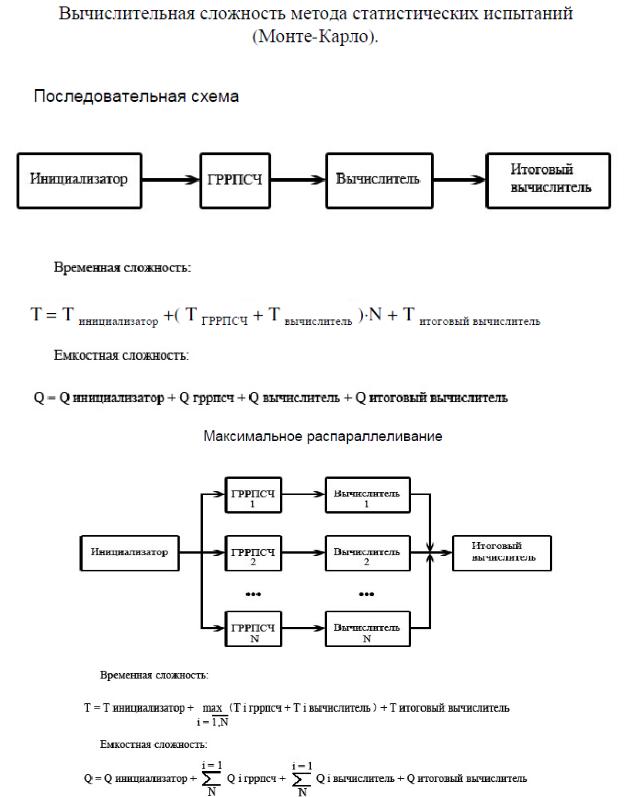
При выполнении вычислений m-мерных интегралов на основе распределенной

модели Монте-Карло с целью снижения ее сложностных оценок целесообразно:

•распараллелить процедуру генерирования m равномерно распределенных псевдослучайных чисел (РРПСЧ) ;

•представить генератор РРПСЧ и вычислитель на базе одного элемента распределенной вычислительной структуры;

•особое внимание уделить снижению сложностных оценок для реализации системы «генератор РРПСЧ - вычислитель».