
Основные понятия математической статистики
.pdf
vk.com/club152685050 | vk.com/id446425943
1.Основные понятия математической статистики. Теоретические и эмпирические оценки начальных и центральных моментов.
Обобщенными числовыми характеристиками для случайных величин в теории вероятностей а также математической статистике являются начальные и центральные моменты. Задачи на отыскание моментов являются неотъемлемой частью теории вероятностей и математической статистики.
Начальным моментом k-го порядка случайной величины Х называют математическое ожидание от величины в k-ой степени 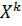 :
: 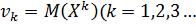
Когда Когда 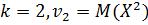 и т. д.
и т. д.
Для дискретной случайной величины X начальные моменты определяют зависимостью
для непрерывной – интегрированием:
Если непрерывная величина задана интервалом 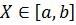 , то моменты вычисляют по формуле
, то моменты вычисляют по формуле 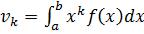
Центральным моментом k-го порядка называют математическое ожидание от величины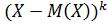 :
: 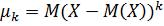
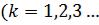 )
)
Когда 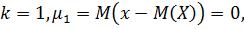 Когда
Когда 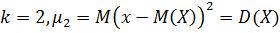
Для дискретной случайной величины центральные моменты вычисляют по формуле
для непрерывной – по формуле
Если случайная величина определена интервалом 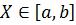 , то центральные моменты определяют интегрированием
, то центральные моменты определяют интегрированием
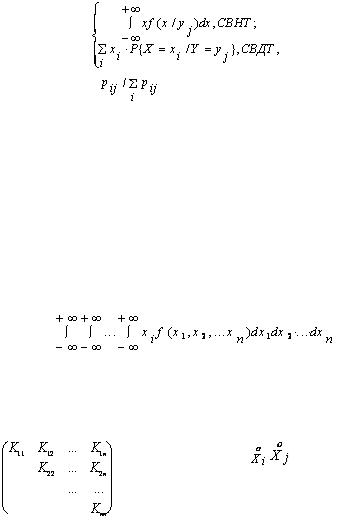
vk.com/club152685050 | vk.com/id446425943
2. Основные понятия математической статистики. Теоретические и эмпирические оценки ковариационных и корреляционных моментов.
Центральный момент m1,1 называется корреляционным моментом (ковариацией):
KXY = M[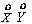 ] = M[(X-mX)×(Y-mY)] = M[XY]-mX mY.
] = M[(X-mX)×(Y-mY)] = M[XY]-mX mY.
Коэффициентом корреляции двух случайных компонентов X и Y случайного вектора является нормированная ковариация
rXY = KXY/(sXsY). Свойства ковариации (и коэффициента корреляции):
1.KXX = DX, KYY = DY, (rXX = rYY = 1);
2.KXY = KYX, (rXY = rYX);
3.|KXY| £ 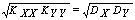 , (|rXY | £ 1).
, (|rXY | £ 1).
Ковариационный момент и коэффициент корреляции определяет степень линейной зависимости между X и Y. Условие |rXY | = 1 необходимо и достаточно, чтобы СВ X и Y были связаны линейной зависимостью Х = a×Y + b, где a и b - константы. СВ, для которых KXY = 0 (rXY = 0), называются некоррелированными. Из независимости случайных величин Х и Y вытекает их некоррелированность (обратное неверно).
Условным математическим ожиданием компоненты Х при условии, что Y приняла одно из своих возможных значений yj, называется действительное число определяемое формулой:
mX/Y = M[X/Y = yj] = |
|
где Р{X = xi /Y = yj} = |
, pij = Р{X = xi ,Y = yj}. |
Условной дисперсией компоненты Х при условии, что Y приняла одно из своих возможных значений yj, называется действительное число определяемое формулой:
DX/Y = D[X/Y = yj] = 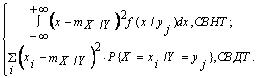
Приведенные выше формулы для числовых характеристик двумерного случайного вектора без труда обобщаются на случай n-мерного случайного вектора (Х1, Х2, ..., Хn). Так, например, вектор с неслучайными координатами (m1, m2, ..., mn), где mi - математическое ожидание СВ Хi, определяемое формулой
mi = M[Xi] = |
, называется центром, рассеивания |
случайного вектора. |
|
Ковариационной матрицей n-мерного случайного вектора 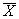 = (Х1, Х2, ..., Хn) называется симметрическая матрица, элементы которой представляют собой ковариации соответствующих пар компонент случайного вектора:
= (Х1, Х2, ..., Хn) называется симметрическая матрица, элементы которой представляют собой ковариации соответствующих пар компонент случайного вектора:
|
где Кij = M[ |
] - ковариация i-й и j-й компонент. |
|
Очевидно, что Кii = М[Xi2] -дисперсия i-й компоненты. |
|
K = |
, |
|
Корреляционной |
матрицей n-мерного |
случайного вектора называется симметрическая |
матрица, составленная из коэффициентов корреляции соответствующих пар компонент случайного вектора:
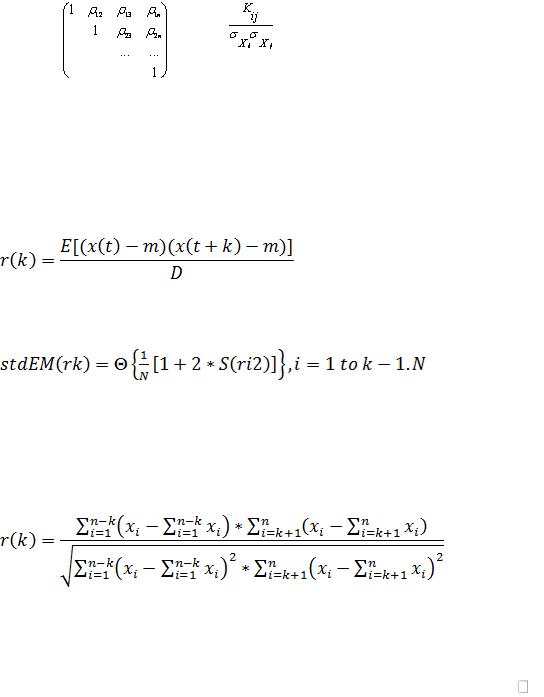
vk.com/club152685050 | vk.com/id446425943
rij = - коэффициент корреляции i-й и j-й компоненты
C = |
, |
3. Основные понятия математической статистики. Теоретические и эмпирические оценки автокорреляции, автокорреляционное расстояние.
Автокорреляция - корреляция ряда X с самим собой, с задержкой на k наблюдений. Пусть X(t) - значение случайного процесса в момент времени t.
Если X(t) имеет среднее значение m и дисперсию D, то вычисление коэффициентов автокорреляции r(k) осуществляется следующим образом.
где "E" - это математическое ожидание.
Предполагая порядок процесса k-1, стандартная ошибка r(k) определяется: - число наблюдений ряда.
В статистике имеется несколько выборочных оценок теоретических значений автокорреляции r(k) процесса по конечному временному ряду из n наблюдений. Наиболее популярной оценкой является нециклический коэффициент автокорреляции с задержкой k:
Наиболее важным из различных коэффициентов автокорреляции является первый - r1, измеряющий тесноту связи между уровнями x(1), x(2) ,..., x(n -1) и x(2), x(3), ..., x(n).
Последовательность коэффициентов корреляции rk , где k 1, 2,...,n , как функция интервала k между наблюдениями называется автокорреляционной функцией (АКФ).
Вид выборочной автокорреляционной функции тесно связан со структурой ряда. Автокорреляционная функция rk для "белого шума", при k >0, также образует стационарный временной ряд со средним значением 0. Для стационарного ряда АКФ быстро убывает с ростом k. При наличии отчетливого тренда автокорреляционная функция приобретает характерный вид очень медленно спадающей кривой. В случае выраженной сезонности в графике АКФ также присутствуют выбросы для запаздываний, кратных периоду сезонности, но эти выбросы могут быть завуалированы присутствием тренда или большой дисперсией случайной компоненты.
vk.com/club152685050 | vk.com/id446425943
4.1) (написать ко всем вопросам с 4 по 9й). Задача кластерного анализа. Методы древовидной кластеризации. Форма представления результатов.
При использовании данных методов возможно поэтапное решение задач многопараметрического анализа, в частности:
1)разбиение множества объектов анализа на группы кластеры;
2)определение достоверности разбиения на кластеры;
3)построение дискриминантных функций по заданному множеству объектов, разделенному на априори заданные группы и набору признаков;
4)определение статистической зависимости – между двумя признаками (корреляции или парной регрессии), между зависимым и двумя и более независимыми признаками (множественной регрессии), а также между реализациями одного и того же признака (автокорреляции);
5)редукция множества признаков из набора путем выделения значимых факторов, описывающих два и более признаков.
Методы кластерного анализа позволяют построить классификации многомерных данных, выявить внутренние связи между единицами наблюдаемой совокупности, а также могут использоваться с целью сжатия информации.
Задача кластеризации.
Пусть множество I ={I1, I 2 ,..I n} обозначает n объектов (индивидов), принадлежащих некоторой популяции 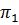 . Предположим также, что существует некоторое множество наблюдаемых показателей или характеристик
. Предположим также, что существует некоторое множество наблюдаемых показателей или характеристик 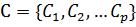 , которыми обладает
, которыми обладает
каждый индивид из I. Наблюдаемые характеристики могут быть как количественными, так и качественными. Результат измерения i-й характеристики I j объекта будем обозначать символом xij , a вектор X j =xij размерности p x1 будет отвечать каждому ряду измерений (для j-го индивида). Таким образом, для множества индивидов I исследователь располагает множеством векторов измерений X ={X1 , X 2 ,..., X n } , которые описывают множество I. Отметим, что множество X может быть представлено как n точек в р-мерном евклидовом пространстве Ep .
Пусть m — целое число, меньшее, чем n. Задача кластерного анализа заключается в том, чтобы на основании данных, содержащихся в множестве X, разбить множество объектов I на m кластеров (подмножеств) π 1 ,π 2 ,...,π m так, чтобы каждый объект Ii принадлежал одному и только одному подмножеству разбиения и чтобы объекты, принадлежащие одному и тому же кластеру, были сходными, в то время как объекты, принадлежащие разным кластерам, были разнородными (не сходными).
Для того чтобы «решить» задачу кластерного анализа, необходимо количественно определить понятия сходства и разнородности. Задача решена, если i-й и j-й объекты попадут в один и тот же кластер, если расстояние (отдаленность) между соответствующими точками X iи X j будет «достаточно малым», и, наоборот, попадут в разные кластеры, если расстояние между точками X I и X j будет «достаточно большим».
vk.com/club152685050 | vk.com/id446425943
Различие (схожесть) объектов определяется на основе понятия расстояния (метрики) d(Xi , X j ) между точками X I и X j .
4.2) (пиши сначала 4.1) Задача кластерного анализа. Методы древовидной кластеризации. Форма представления результатов.
Иерархический кластерный анализ
Сущность этих методов заключается в том, что на первом шаге каждый объект выборки рассматривается как отдельный кластер. Процесс объединения кластеров происходит последовательно: на основании матрицы расстояний или матрицы сходства объединяются наиболее близкие объекты. Если матрица сходства первоначально имеет размерность m х m, то полностью процесс кластеризации завершается за m
– 1 шагов, в итоге все объекты будут объединены в один кластер.
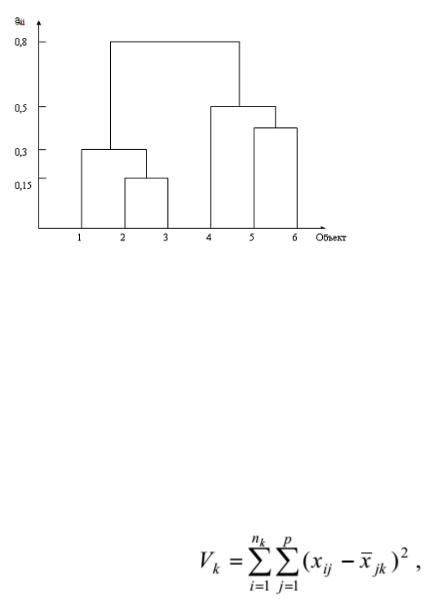
Дендрограмма (dendrogram) - древовидная диаграмма, содержащая n уровней, каждый из которых соответствует одному из шагов процесса последовательного укрупнения кластеров. На дендрограмме указываются номера объединяемых объектов и расстояние (или иная мера сходства), при котором произошло
объединение (рис. 1.1).
Множество методов иерархического кластерного анализа различается не только используемыми мерами сходства (различия), но и алгоритмами классификации. Из них наиболее распространены метод одиночной связи, метод полных связей, метод средней связи, метод Уорда.
Метод полных связей (Complete linkage).
Включение нового объекта в кластер происходит только в том случае, если расстояние между объектами не меньше некоторого заданного уровня.
Метод средней связи.
Для решения вопроса о включении нового объекта в уже существующий кластер вычисляется среднее значение меры сходства, ко-торое затем сравнивается с заданным пороговым уровнем. Если речь идет об объединении двух кластеров, то вычисляют расстояние между их центрами и сравнивают пороговым значением
Метод Уорда. Данный метод предполагает, что на первом шаге каждый кластер состоит из одного объекта. Первоначально объединяются два ближай-ших кластера. Для них определяются средние значения каждого признака и рассчитывается сумма
квадратов отклонений
vk.com/club152685050 | vk.com/id446425943
где k - номер кластера, i - номер объекта, j - номер признака, p - количество признаков, характеризующих каждый объект, kn — количество объектов в k-м кластере.
5) (пиши сначала 4.1) Задача кластерного анализа. Метод k-средних. Форма представления результатов.
Предположим, мы уже имеем гипотезы относительно числа кластеров (по наблюдениям или по переменным). Вы можете указать системе образовать ровно три кластера так, чтобы они были настолько различны, насколько это возможно. Это именно тот тип задач, которые решает алгоритм метода k-средних.
В общем случае метод k-средних строит ровно K различных кластеров, расположенных на возможно больших расстояниях друг от друга. Сущность их заключается в том, что процесс классификации начинается с задания некоторых начальных условий (количество образуемых кластеров, порог завершения процесса классификации и т. д.).
Целесообразно сначала провести классификацию по одному из иерархических методов или на основании экспертных оценок, а затем уже подбирать начальное разбиение и статистический критерий для работы итерационного алгоритма.
В отличие от иерархических процедур метод k-средних не требует вычисления и хранения матрицы расстояний или сходств между объектами. Алгоритм этого метода предполагает использование только исходных значений переменных. Для начала процедуры классификации должны быть заданы k случайно выбранных объектов, которые будут служить эталонами, т.е. центрами кластеров. Считается, что алгоритмы эталонного типа удобные и быстродействующие. В этом случае важную роль играет выбор начальных условий, которые влияют на длительность процесса классификации и на его результаты.
С вычислительной точки зрения можно рассматривать этот метод, как дисперсионный анализ "наоборот". Программа начинает с K случайно выбранных кластеров, а затем изменяет принадлежность объектов к ним, чтобы: 1) - минимизировать изменчивость внутри кластеров, и 2) - максимизировать изменчивость между кластерами.
Обычно, когда результаты кластерного анализа методом к- средних получены, можно рассчитать средние для каждого кластера по каждому измерению, чтобы оценить, насколько кластеры различаются друг от друга. В идеале вы должны получить сильно различающиеся средние для большинства, если не для всех измерений, используемых в анализе. Значения F-статистики, полученные для каждого измерения, являются другим индикатором того, насколько хорошо соответствующее измерение дискриминирует кластеры.
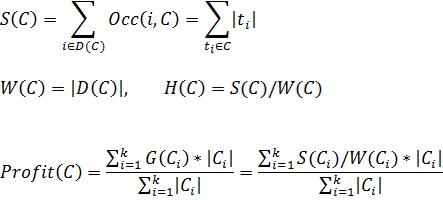
vk.com/club152685050 | vk.com/id446425943
6. (пиши сначала 4.1)Методы многопараметрического анализа. Задача кластерного анализа. Алгоритм CLOPE: критерий разделения на кластеры, градиент, функция стоимости
Алгоритм CLOPE.
Назначение: кластеризация огромных наборов категорийных данных. Достоинства: высокие масштабируемость и скорость работы, а так же качество
кластеризации, что достигается использованием глобального критерия оптимизации на основе максимизации градиента высоты гистограммы кластера. Он легко рассчитывается и интерпретируется. Во время работы алгоритм хранит в RAM небольшое количество информации по каждому кластеру и требует минимальное число сканирований набора данных. CLOPE автоматически подбирает количество кластеров, причем это регулируется одним единственным параметром – коэффициентом отталкивания. Описание алгоритма [2]:
Пусть имеется база транзакций D, состоящая из множества транзакций {t1,t2,…,tn}. Каждая транзакция есть набор объектов {i1,…,im}. Множество кластеров {C1,…,Ck}
есть разбиение множества {t1,…,tn}, такое, что C1 U … U Ck={t1,…,tn} и Ci <> Ø и Сi ∩
Cj = Ø i ≥ 1, k ≥ j. Каждый элемент Ci
называется кластером, а n, m, k – количество транзакций, количество объектов в базе транзакций и число кластеров соответственно.
Каждый кластер C имеет следующие характеристики: D(C) – множество уникальных объектов;
Occ(i,C) – количество вхождений (частота) объекта i в кластер C;
Функция стоимости:
Где  - количество объектов в i-ом кластере, k – количество кластеров, r –
- количество объектов в i-ом кластере, k – количество кластеров, r –
коэффициент отталкивания (0 < r ≤ 1).
С помощью параметра r регулируется уровень сходства транзакций внутри кластера, и, как следствие, финальное количество кластеров. Этот коэффициент подбирается пользователем. Чем больше r, тем ниже уровень сходства и тем больше кластеров будет сгенерировано.
Формальная постановка задачи кластеризации алгоритмом CLOPE выглядит следующим образом:
для заданных D и r найти разбиение C: Рrofit(C, r)→max .
vk.com/club152685050 | vk.com/id446425943
7. (пиши сначала 4.1) Методы многопараметрического анализа. Задача кластерного анализа. Алгоритм CLOPE: этапы алгоритма кластеризации, задача кластеризации по алгоритму, вычислительная сложность алгоритма.
Рассмотрим реализацию алгоритма. Пусть поисковые профили хранятся в таблице базы данных. Для построения начального разбиения, определяемого функцией Profit(C,r) требуется первый проход по таблице профилей. После этого требуется незначительное (1-3) количество дополнительных сканирований таблицы для повышения качества кластеризации и оптимизации функции стоимости. Если в текущем проходе по таблице, изменений не произошло, то алгоритм прекращает свою работу.
При построении начального разбиения из таблицы читается очередной профиль и создается новый кластер (отдельная таблица) или помещается в уже существующий кластер, который дает максимум Profit(C,r).
На итерационном этапе просматривается таблица профилей и для каждого профиля решается задача определения кластера, если новый
кластер 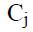 максимизирует Profit(C,r), то профиль переносится в этот кластер. В начале каждого цикла устанавливается индикатор перемещения moved := false. Если в цикле происходит перемещение профиля индикатор перемещения изменяется moved :=true. Итерации завершаются, если значение moved=false не изменится. После завершения итераций удаляются все пустые кластеры.
максимизирует Profit(C,r), то профиль переносится в этот кластер. В начале каждого цикла устанавливается индикатор перемещения moved := false. Если в цикле происходит перемещение профиля индикатор перемещения изменяется moved :=true. Итерации завершаются, если значение moved=false не изменится. После завершения итераций удаляются все пустые кластеры.
Алгоритм CLOPE является масштабируемым, поскольку способен работать в ограниченном объеме оперативной памяти компьютера. Во время работы в оперативной памяти хранится только текущая транзакция и небольшое количество информации по каждому кластеру, которая состоит из: количества транзакций N, числа уникальных объектов (или ширины кластера) W, простой хэш-таблицы для расчета Occ(i,C) и значения S площади кластера.
В результате кластеризации поисковый профиль конечного пользователя i окажется в определенном кластере 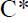 .
.
Для предъявления пользователю не просмотренных страниц, соответствующих постоянной информационной потребности, производится расширение его поискового профиля. Для этого поисковые запросы, входящие в состав кластера C*, ранжируются по частоте их вхождения в кластер. В расширенный поисковый профиль выбирается некоторое количество lm поисковых запросов с наибольшей частотой вхождения.
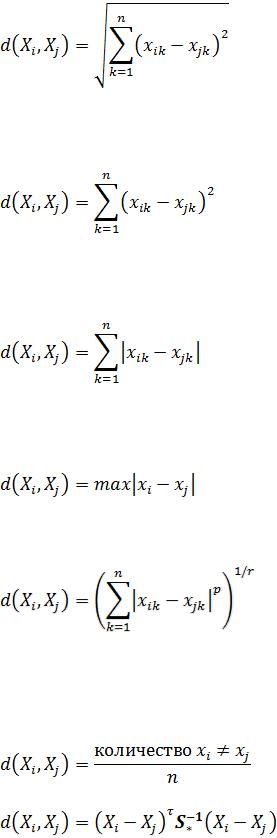
vk.com/club152685050 | vk.com/id446425943
8.(пиши сначала 4.1) Меры расстояния между объектами (метрики).
Вкластерном анализе используются различные меры расстояния
d(Xi , X j )между объектами:
Евклидово расстояние(Euclidean distances):
Квадрат евклидова расстояния (Squared Euclidean distances). Стандартное евклидово расстояние возводят в квадрат, если нужно придать большие веса более отдаленным друг от друга объектам. Это расстояние вычисляется следующим образом:
Расстояние городских кварталов (манхэттенское расстояние, City-block distances). Это расстояние является просто средним разностей по координатам. В большинстве случаев эта мера расстояния приводит к таким же результатам, как и для обычного расстояния Евклида. Манхэттенское расстояние вычисляется по формуле:
Расстояние Чебышева (Chebychev distance metric). Это расстояние может оказаться полезным, когда желают определить два объекта как "различные", если они различаются по какой-либо одной координате (каким-либо одним измерением). Расстояние Чебышева вычисляется по формуле:
Степенное расстояние. Иногда желают прогрессивно увеличить или уменьшить вес, относящийся к размерности, для которой соответствующие объекты сильно отличаются. Степенное расстояние вычисляется по формуле:
где r и p - параметры, определяемые пользователем.
Процент несогласия (percent disagreement). Эта мера используется в тех случаях, когда данные являются категориальными. Это расстояние вычисляется по формуле:
Расстояние Махаланобиса:
где xik , x jk - значения k-й переменной i-го и j-го объекта; Xi , X j - векторы значений переменных у i-го и j-го объектов; S* - общая ковариационная матрица.
vk.com/club152685050 | vk.com/id446425943
9. (пиши сначала 4.1) Методы многопараметрического анализа. Задача кластерного анализа. Проверка достоверности кластеризации: критерии, дискриминантный анализ.
Дискриминантный анализ (ДА) является статистическим методом, который позволяет изучать различия между двумя и более группами объектов по нескольким переменным одновременно. ДА помогает выявлять различия между группами и дает возможность идентифицировать (классифицировать) объекты по принципу максимального сходства.
Характеристики, применяемые для того, чтобы отличать один класс от другого называются дискриминантными переменными. Эти переменные должны измеряться либо по интервальной шкале, либо по шкале отношений. В общем случае, число дискриминантных переменных не ограничено, но в сумме число объектов должно всегда превышать число переменных по крайней мере на два.
Объекты анализа должны принадлежать одному из двух или более классов. Класс должен быть определен таким образом, чтобы каждое наблюдение принадлежало одному и только одному классу. Допускаются и объекты, которые нельзя отнести ни к одной из групп (классов). Такие объекты будут классифицироваться позже, на основе математических функций, полученных из анализа наблюдений с известной принадлежностью.
Все процедуры дискриминантного анализа можно разбить на две группы: первая группа позволяет интерпретировать различия между имеющимися группами
(сравнивая средние), вторая – проводить классификацию новых объектов в тех случаях, когда неизвестно заранее, к какому из существующих классов они принадлежат.
Для двух групп дискриминантный анализ может рассматриваться также как процедура множественной регрессии. Если кодируются две группы как 1 и 2, и затем используются эти переменные в качестве зависимых переменных в
множественной регрессии, то получится результаты, аналогичные тем, которые получили бы с помощью Дискриминантного анализа.
группа = a + b1x1 + b2 x2 + ...+ bm xm , (2.6) где a является константой, и b1...bm являются коэффициентами регрессии. Интерпретация результатов задачи с двумя совокупностями тесно следует логике применения множественной регрессии: переменные с наибольшими регрессионными коэффициентами вносят наибольший вклад в дискриминацию.
