8. Функциональные преобразования случайных величин

1. Сформулировать задачу преобразования случайных величин.

Пусть есть СВ Є которая имеет ФР F_є(x). Пусть задана y=G(x), тогда n=G(Є). Надо найти F_n(y), F_є(x)->F_n(y)

2. Привести общий подход к решению задачи преобразования случайной величины

Зафиксируэм точку y=y₀: P₀= F_η(y)=P{η<y}

Определим области возможных значений СВ ξ, из которых получается значение СВ η<y

F _η(y)=P{ η<y}=P{ξ<x₁}+P{x₂<ξ<x₃}=F_ξ(x₁)+[F_ξ(x₃)-F_ξ(x₂)]

3. Какие проблемы существуют при решении задачи преобразования случайных величин?

Основной проблемой при решении задачи преобразования случайных величин является то, что в большинстве случаев х_к не могут быть полученые

В явном виде аналитически.

Поскольку yє(-∞;∞) меняется место расположения и кол-во х_к

Решение зависит от вида ф-и распределения F ξ₍x)

4. Какие условия накладываются на функцию преобразования для получения решения задачи преобразования случайных величин в явном виде?

а)Монотонное преобразование. y=G(x)монотонно возрастает ф-ция

F_η(y)=P{η<y}=P{ξ<x}=P{ ξ < G^-1(y)}=F_ξ(G^-1(y))

б)Монотонно спадает F_η(y)=P{η<y}=P{ξ≥x}=1-P{ ξ<x }=1-F_ξ(G^-1(y)+0)

5. Привести формулу для функции распределения случайной величины, полученной непрерывным монотонным преобразованием.

П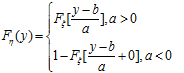 ривести формулу для функции распределения случайной величины, полученной линейным преобразованием.

Линейное преобразование не меняет вида закона распределения,поэтому случайные величины ξ и η распределены одинаково, но с различными параметрами.

6. Привести формулу для плотности вероятностей случайной величины, полученной непрерывным монотонным преобразованием.

7. Привести формулу для плотности вероятностей случайной величины, полученной линейным преобразованием.

8. Чему равна плотность вероятностей суммы непрерывных случайных величин?

9. Чему равна плотность вероятностей разности двух непрерывных случайных величин?

10. Чему равна плотность вероятностей произведения двух непрерывных случайных величин?

11. Чему равна плотность вероятностей частного двух непрерывных случайных величин?

9. Числовые характеристики случайной величины

1. Дать определение математического ожидания случайной величины.

М ат. ожидание СВ.  с функцией распределения F(x) называется действительное число m, определяемое следующей формулой

если указанный интеграл абсолютно сходится.

2. Привести формулу для вычисления математического ожидания дискретных случайных величин.

если указанный ряд абсолютно сходится

3. Привести формулу для вычисления математического ожидания непрерывных случайных величин.

4. Привести формулу для вычисления математического ожидания смешанных случайных величин.

5. Перечислить основные свойства математического ожидания.

1. Математическое ожидание константы равно этой константе М{с} = с.

2. Константу можно вынести за знак математического ожидания: M{с ξ} = с M{ξ}.

3. Математическое ожидание суммы любых случайных величин ξ и η равно сумме их математических ожиданий.

E (ξ + η ) = E (ξ )+ E (η)

4. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий.: если ξ и η независимы, то E(ξη) = Eξ* Eη.

5. Значение мат. ожидания для дискретних величин не обезательно должна совпадать с каким либо значением этих величин.

6. [М{ξ}]=[ξ]

6. Чему равно математическое ожидание постоянной величины? Доказать.

С выроджена СВ принимающяя одно значение с вероятностью 1 .m=∑x_ip_i=c*1

7. Чему равно математическое ожидание произведения постоянной и случайной величины? Доказать.

M{c ξ }=∑(c*1)x_jp_j=c∑(x_jp_j)=cM{ ξ }

8. Чему равно математическое ожидание суммы случайных величин? Доказать.

M{ ξ1+ξ2 }=∑_i∑_j(x_i+x_j)p_ij=∑x_1i∑p_ij+∑x_2j∑p_ij = ∑x_1i∑p_i+∑x_2j∑p_i = M{ ξ₁} + M{ ξ₂ }

9. Чему равно математическое ожидание произведения независимых случайных величин? Доказать.

M{ ξ1 ξ2 }=∑_i∑_j(x_i x_j)p_ij=∑_i ∑_j x_i X_j p_ij = ∑_ix_ip_i ∑_jx_j∑p_j = M{ ξ₁} M{ ξ₂ }

10. Какой смысл имеет математическое ожидание случайной величины?

МО – среднее значение СВ, которое не всегда совпадает со значением дискретной СВ.

11. Какие единицы измерения имеет математическое ожидание? Обосновать ответ.

МО является линейной функцией от СВ., (вероятность не имеет размерности) имеет размерность СВ.

12. Как определяется дисперсия случайной величины?

Дисперсия Dξ = E(ξ – Eξ)² есть «среднее значение квадрата отклонения случайной величины ξ от своего среднего значения».

13. Привести формулу для вычисления дисперсии дискретных случайных величин.

14. Привести формулу для вычисления дисперсии непрерывных случайных величин.

15. Привести формулу для вычисления дисперсии смешанных случайных величин.

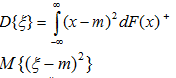
16. Какой смысл имеет дисперсия случайной величины?

Если говорить о распределении случайной величины, как о распределении единичной массы по невесомому стержню, то дисперсия есть в точности момент инерции этого стержня, закрепленного в центре тяжести.

Kоличественная характеристика разброса значений случайной величины.

17. Перечислить основные свойства дисперсии.

1)дисперсия от константы равна 0. D{c}=0

2) константа выносится за знак дисперсии и возносится в квадрат

3) Если ξ и η независимы, то

Действительно,

так как математическое ожидание произведения независимых с.в. равно произведению их математических ожиданий.

4)  - Средне Квадратическое Отклонение

18. Чему равна дисперсия постоянной величины? Доказать.

По определению дисперсии D{ξ}=M{(с-М{c})²}= M{(с-c)²}= M{0}=0

19. Чему равна дисперсия случайной величины, умноженной на постоянную величину? Доказать.

На основании определения дисперсии D{ξ}=M{(ξ-m})²} и свойства мат ожид M{сξ}=с M{ξ} имеем D{сξ}=M{(сξ-М{cx})²}=M{(cx-cM{x})²}=M{c²(x-M{x})²}=c²M{(c-M{x})²}=c²D{ξ}

20. Чему равна дисперсия суммы независимых случайных величин? Доказать.

D{ξ₁+ ξ₂}=M{((ξ₁+ξ₂)-М{ξ₁+ ξ₂})²}=M{(ξ₁–M{ξ₁})²+2М{(ξ₁–M{ξ₁})(ξ₂–M{ξ₂})+(ξ₂–M{ξ₂})²}=D{ ξ₁}+D{ξ₂}

21. Какие единицы измерения дисперсии?

Единицы измерения такие же как у СВ. возведенные в квадрат. [D{ξ}]=[ξ²]

22. Дать определение среднего квадратического отклонения. Какие единицы измерения среднего квадратического отклонения?

СКО величина численно равная корню квадратному из дисперсии , характеризует пологость графика плотности вероятности. (чем больше тем график более пологий). Размерность: совпадает с СВ.

23. Чему равно среднее квадратическое отклонение суммы двух независимых случайных величин?

24. Записать неравенства Чебышева.

25. Как определяется центрированная случайная величина?

Значение СВ минус ее мат ожидание

26. Чему равно математическое ожидание центрированной случайной величины? Доказать.

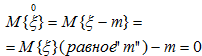
27. Чему равна дисперсия центрированной случайной величины? Доказать.

28. Как определяется нормированная случайная величина?

29. Чему равно математическое ожидание нормированной случайной величины? Доказать.

30. Чему равна дисперсия нормированной случайной величины? Доказать.

31. Как определяется стандартная случайная величина?

Как СВ. с нулевым. МО. и единичной дисперсией.

32. Чему равно математическое ожидание стандартной случайной величины? Доказать.

33. Чему равна дисперсия стандартной случайной величины? Доказать.

34. Дать определение начальных моментов случайной величины.

Начальным моментом порядка «к» СВ.  с ФР. F(x), наз. Действительное число α_k которое определяется

35. Дать определение центральных моментов случайной величины.

36. Какие единицы измерения начальных моментов случайной величины?

Как и у МО

37. Какие единицы измерения центральных моментов случайной величины?

Как у дисперсии

38. Записать формулу для вычисления начальных моментов дискретных случайных величин.

39. Записать формулу для вычисления начальных моментов непрерывных случайных величин.

40. Записать формулу для вычисления центральных моментов дискретных случайных величин.

41. Записать формулу для вычисления центральных моментов непрерывных случайных величин.

42. Записать формулу, выражающую дисперсию через начальные моменты случайной величины.

43. Дать определение коэффициента асимметрии.

44. Какой смысл коэффициента асимметрии?

Является мерой ассиметричности распределения

45. Дать определение коэффициента эксцесса.

46. Какой смысл коэффициента эксцесса?

Х-зует меру затянутости хвостового распределения. Х-зует степень островершимости p(x) по сравнению с Гаусом, х-зует скорость убывания хвостов.