2. Дать определение закона распределения случайной величины.

Поскольку значения числовых характеристик схем испытания соответствуют в схеме некоторым случайным событиям (с их определёнными вероятностями), то и сами эти значения являются случайными (с теми же вероятностями). Поэтому такие числовые характеристики и принято называть случайными величинами. При этом расклад вероятностей по значениям случайной величины называется законом распределения случайной величины.

3. Дать определение функции распределения случайной величины.

Функцией распределения СВ назыв вероятность того что СВ не приймет значений больших наперед заданного числа.

Для любого x: A={ро(как густина) < альфа} < F

Тогда функция распределения случайных величин пси F(x), называется вероятность того, что значение СВ пси будут менше некоторого заданного значения x. F(x) = P { пси < x }

4. Перечислить основные свойства функции распределения случайной величины.

1)непрерывна слева F(x) = P(ξ<x)

2)неспадающая x₁ = x₂ F(x₁) <= F(x₂)

3)

4) P(a<= ξ <b)=F(b)-F(a)

5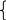 )P(ξ=x0) = 0, x0 - непрерывность

P₀, x0 – точка разрыва

6) {F()x} = 1 – безразмерная величина

5. Как с помощью функции распределения вычислить вероятность попадания случайной величины в заданный интервал?

P(a<= ξ <b)=F(b)-F(a)

6. Чему равна вероятность того, что случайная величина примет конкретное значение? Обосновать ответ.

Вероятность того, что непрерывная случайная величина примет конкретное значение равна нулю: .

7. Какие единицы измерения имеет функция распределения? Обосновать ответ.

Безразмерные. Так как ф-я распределения характеризует вероятность относящуюся к СВ.

8. Какие виды случайных величин существуют?

1) дискретные

2) непрерывные

3) смешанные

9. Привести примерные графики функции распределения для различных видов случайных величин.

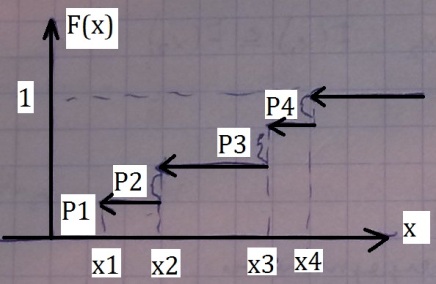
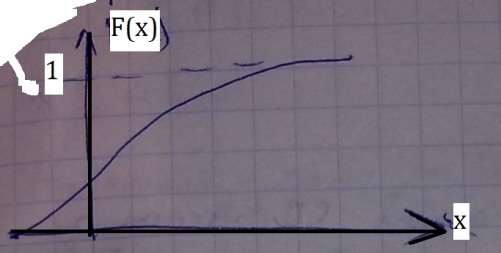
10. Что такое ряд распределения?

Ряд распределения строится по функции распределения для дискретных значений. Это соответствие значениям СВ соответственных вероятностей.

11. Что называется плотностью вероятностей?

Производная от ФР

12. Перечислить основные свойства плотности вероятностей.

1) F(x)=

2) p(x) >= 0 – неотрицательность

3) – свойство нормировки

4) P (a<=ξ<=b)=

5) [p(x)]= 1/ [ξ]

13. Какие единицы измерения имеет плотность вероятностей? Обосновать ответ.

Плотность вероятности имеет размерность обратную размерности случайной величины. Если случайная величина в м, то плотность вероятности в 1/м и т.д.

Обоснование: [p(x)]= 1/ [ξ]

14. Имеются ли ограничения на максимальное значение плотности вероятностей? Обосновать ответ.

Не имеется

Обоснование: [p(x)]= 1/ [ξ]

15. Как с помощью плотности вероятностей найти вероятность попадания случайной величины в заданный интервал?

Берем интеграл от плотности вероятности с границами самого интервала и получаем разницу значений ФР в этих точка, что по свойствам ФР равно вероятности.

16. Как с помощью плотности вероятностей найти функцию распределения?

Взять интеграл по пределам ФР.