
- •М.А. Айгунян
- •Аппарат линейной перспективы
- •Перспектива прямых частного положения
- •Метрические задачи в перспективе
- •Измерение отрезков
- •Построение перспективы точки по координатам
- •Перспективный масштаб
- •Деление отрезка
- •Проведение параллельных прямых
- •Построение окружностей в перспективе
- •Перспектива окружности, расположенной в предметной плоскости
- •Деление окружности на равные части
- •Перспектива концентрической горизонтальной окружности
- •Перспектива окружности, соосной с горизонтальной окружностью равного радиуса
- •Перспектива окружности, соосной с горизонтальной окружностью другого радиуса
- •Перспектива нескольких соосных горизонтальных окружностей равного радиуса
- •Перспектива соосных окружностей, расположенных в плоскостях, параллельных картинной плоскости
- •Перспектива соосных окружностей, расположенных в плоскостях, перпендикулярных картинной плоскости
- •Перспектива соосных окружностей, расположенных в параллельных вертикальных плоскостях
- •Выбор точки зрения
- •Методы построения перспективы
- •Метод архитекторов
- •Радиальный метод
- •Метод совмещенных высот
- •Координатный метод
- •Метод перспективной сетки
- •Перспектива интерьера
- •Тени в перспективе
- •Отражения в перспективе
- •Перспектива на наклонной плоскости
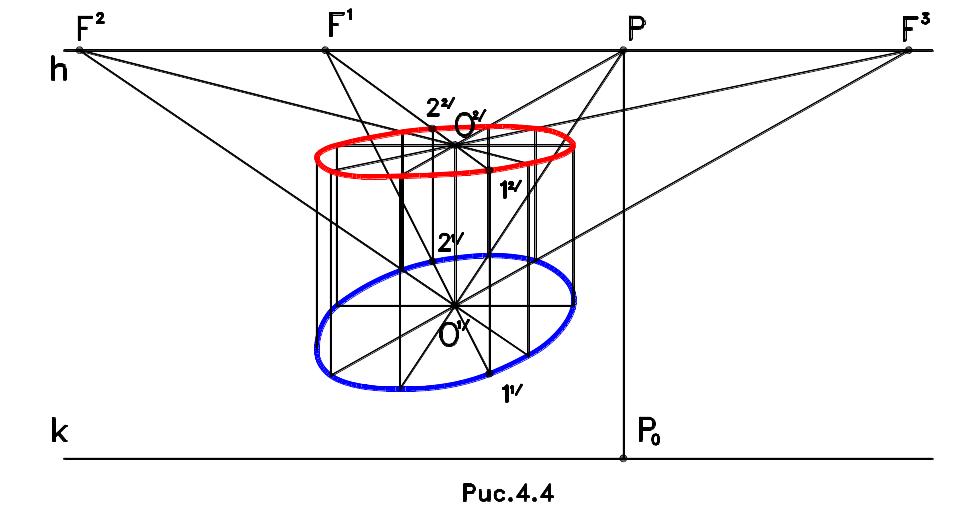
Перспектива окружности, соосной с горизонтальной окружностью равного радиуса
По заданной перспективе окружности, расположенной в горизонтальной плоскости, можно построить окружность в другой горизонтальной плоскости с таким же радиусом и центром на вертикальной прямой, проходящей через точку O2/ (рис.4.4). Для этого через точки O1/ и O2/ проводятся параллельные горизонтальные прямые и определяется их точка схода. Вертикальная прямая, проведенная из точки пересечения нижней прямой с исходной окружностью 11/, пересекает верхнюю прямую в точке 12/, которая будет лежать на искомой окружности. Таким образом можно построить ряд точек. При этом удобно использовать прямые, которые имеют точку схода главную точку P и дистанционные точки D1 и D2.
Перспектива окружности, соосной с горизонтальной окружностью другого радиуса
По заданной перспективе горизонтальной окружности с центром в точке O1/ можно построить перспективу другой горизонтальной окружности с центром в точке O2/, расположенным на той же вертикали, что и точка O1/, и проходящей через какую-либо заданную точку (например, точку 12/) (рис.4.5). Для этого через точку 12/ и точку O2/ проводится прямая. На этой прямой будет находиться какой-то из диаметров искомой окружности, а ее точка схода F1 (как для горизонтальной прямой) будет находиться на линии горизонта h. На прямой, проведенной из точки схода F1 через точку O1/, будет находиться диаметр заданной окружности 11/21/, параллельный диаметру искомой окружности, проходящему через точку 12/. Если через точки 11/ и 12/ провести прямую до пересечения с продолжением вертикали O1/O2/, то полученная точка S/ будет вершиной конуса вращения, для которого обе окружности являются параллелями, а прямая 11/21/ образующей. Прямая, проведенная через точки 21/ и S/, также является образующей. Ее продолжение в пересечении с продолжением прямой 12/O2/ даст точку 22/, лежащую на искомой окружности. Аналогичным образом можно построить ряд точек, лежащих на искомой окружности, кроме тех которые совпадают с вертикалью.

Перспектива нескольких соосных горизонтальных окружностей равного радиуса
Задана окружность с центром в точке O1/ и необходимо построить окружность с центрами в точках O2/, O3/ и т.д. (рис.4.6). Для этого малая ось эллипса выносится в сторону (на чертеже вправо), точки O, A и B соединяются с точкой Oh на линии горизонта. Величина вертикального отрезка CE, заключенного между полученными прямыми, является малой осью эллипса, являющегося проекцией окружности с центром в точке O3/. Аналогичным образом можно построить перспективу любой окружности того же радиуса с центрами на той же вертикали. На этом чертеже можно наблюдать, так называемое, «раскрытие эллипсов».

Перспектива соосных окружностей, расположенных в плоскостях, параллельных картинной плоскости
Окружность, расположенная в плоскости, параллельной картинной, в перспективе также является окружностью. На рис.4.7 построен ряд соосных окружностей с центрами O1/, O2/, O3/. Прямые 1/P и 2/P позволяют определить диаметры остальных окружностей по заданному диаметру 1-2.
