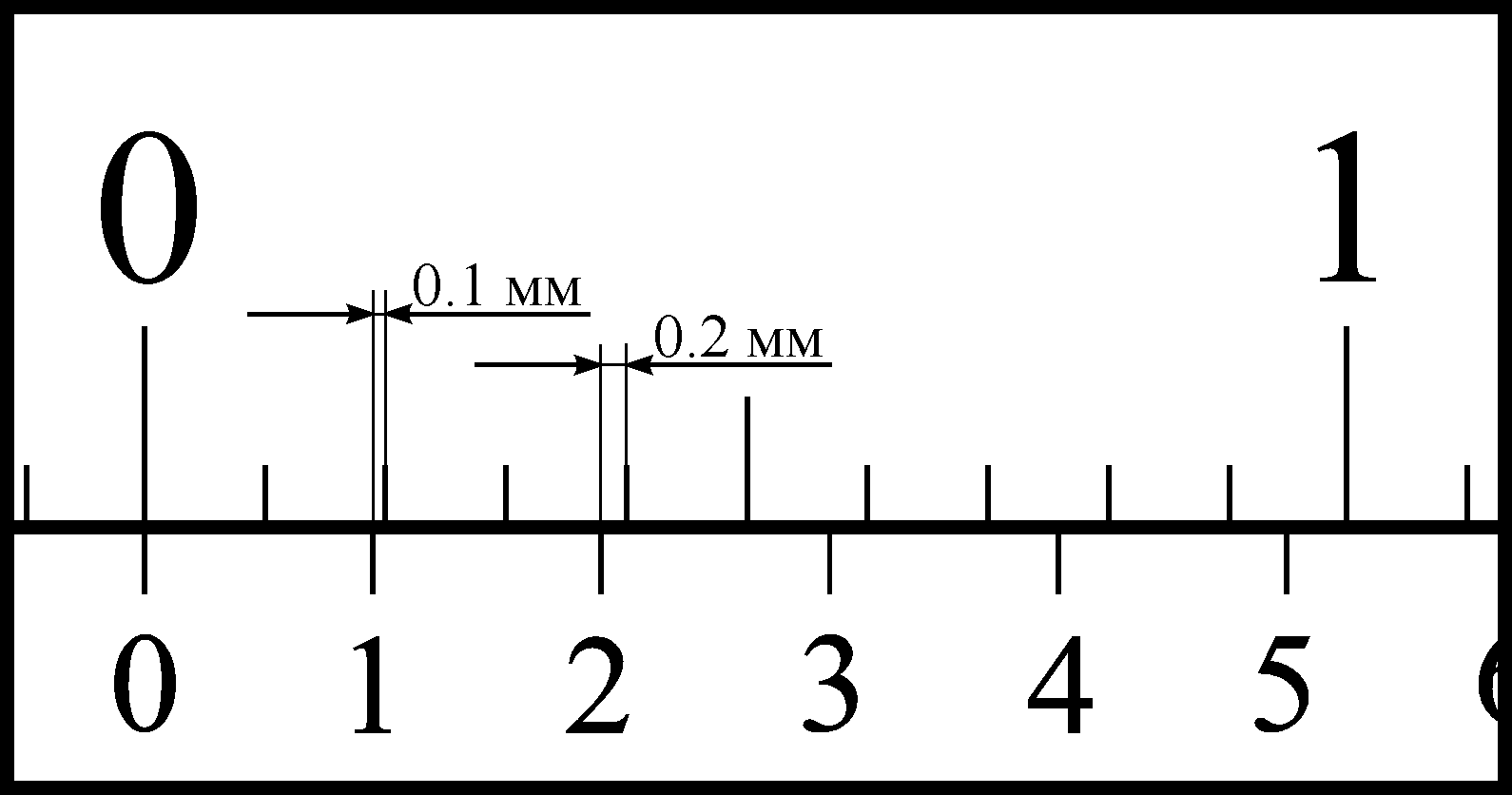- •Механика и молекулярная физика
- •Раздел 1. Подготовка, выполненИе и оформление отчета по лабораторнЫм рабоТам 6
- •Раздел 2. Обработка результатов измерений 9
- •Раздел 3. Лабораторные работы по механике и молекулярНой физиКе 26
- •Введение
- •Раздел 1. Подготовка, выполненИе и оформление отчета по лабораторнЫм рабоТам Подготовка к лабораторному практикуму
- •Правила выполнения и оформления лабораторных работ
- •Раздел 2. Обработка результатов измерений Виды измерений
- •Классификация ошибок
- •Обработка результатов прямого измерения
- •Округление результатов
- •Обработка результатов косвенного измерения
- •Метод наименьших квадратов
- •Раздел 3. Лабораторные работы по механике и молекулярНой физиКе Лабораторная работа № 1
- •Цели и задачи работы
- •Теоретическая часть
- •Штангенциркуль.
- •Микрометр.
- •Определение плотности однородного тела
- •Порядок выполнения работы
- •Определение плотности параллелепипеда
- •Определение плотности цилиндра (шара)
- •Контрольные вопросы
- •Лабораторная работа № 2
- •Цели и задачи работы
- •Теоретическая часть
- •Момент инерции, теорема Штейнера
- •Метод трифилярного подвеса
- •Приборы и принадлежности
- •Порядок выполнения работы
- •Определение момента инерции ненагруженного диска
- •Определение момента инерции сплошного цилиндра относительно оси, проходящей через центр масс тела
- •Проверка теоремы Штейнера
- •Проверка зависимости момента инерции от распределения массы тела относительно оси вращения
- •Контрольные вопросы
- •Лабораторная работа № 3
- •Цели и задачи работы
- •Теоретическая часть
- •3.2.1. Ускорение силы тяжести
- •3.2.2. Описание установки
- •Приборы и принадлежности
- •Порядок выполнения работы
- •3.4.1. Определение ускорения силы тяжести
- •Контрольные вопросы
- •Лабораторная работа № 4
- •Цели и задачи работы
- •Теоретическая часть
- •4.2.1. Основное уравнение динамики вращательного движения, момент силы, момент инерции
- •4.2.2. Маятник Обербека
- •Приборы и принадлежности
- •Порядок выполнения работы
- •4.4.1. Проверка зависимости углового ускорения от момента силы при постоянном моменте инерции
- •4.4.2. Проверка зависимости момента инерции грузов от расстояния до оси вращения
- •Контрольные вопросы
- •Лабораторная работа № 5
- •Цели и задачи работы
- •Теоретическая часть
- •5.2.1. Математический маятник
- •5.2.2. Физический маятник
- •5.2.3. Описание лабораторной установки
- •Приборы и принадлежности
- •Порядок выполнения работы
- •5.4.1. Определение ускорения свободного падения при помощи математического маятника
- •5.4.2. Определение момента инерции физического маятника
- •5.4.3. Определение момента инерции физического маятника в зависимости от распределения массы
- •Контрольные вопросы
- •Лабораторная работа № 6
- •Цели и задачи работы
- •Теоретическая часть
- •6.2.1. Закон Гука
- •6.2.2. Описание лабораторной установки
- •Приборы и принадлежности
- •Порядок выполнения работы
- •Контрольные вопросы
- •Лабораторная работа № 7
- •Цели и задачи работы
- •Теоретическая часть
- •7.2.1. Теплоемкость, коэффициент Пуассона
- •7.2.2. Описание и теория метода
- •Приборы и принадлежности
- •Порядок выполнения работы
- •Контрольные вопросы
Раздел 3. Лабораторные работы по механике и молекулярНой физиКе Лабораторная работа № 1
Определение плотности твердых тел правильной геометрической формы
Цели и задачи работы
Цели работы:
Изучение устройства штангенциркуля и микрометра.
Измерение геометрических размеров тел с помощью измерительных приборов.
Освоение методики взвешивания на аналитических весах.
Задачи работы:
Определение плотности однородного тела цилиндрической формы и формы параллелепипеда.
Определение погрешности измерений.
Теоретическая часть
Для более точных измерений геометрических размеров тел применяется штангенциркуль и микрометр.
Штангенциркуль.
Штангенциркуль
служит для измерения наружных и внутренних
размеров тел с точностью до
![]() .
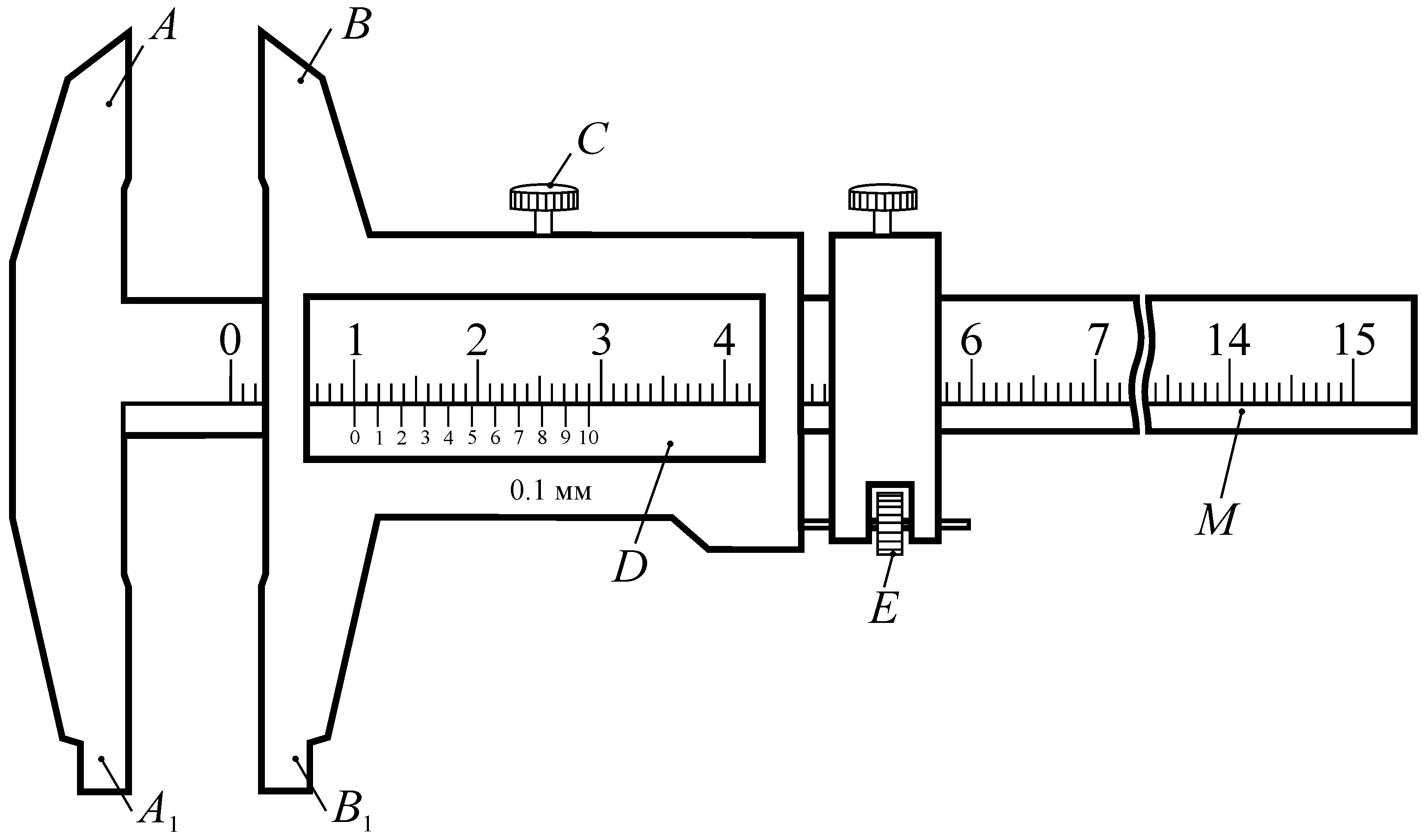
Он состоит из прочной негнущейся
масштабной линейки М
(рис. 2), с одной стороны которой имеется
неподвижная ножка
.
Он состоит из прочной негнущейся
масштабной линейки М
(рис. 2), с одной стороны которой имеется
неподвижная ножка
![]() ,
и подвижной рамки с ножкой
,
и подвижной рамки с ножкой![]() .
В подвижной рамке укреплена вспомогательная
шкала – линейный нониус D,
с помощью которого производят отсчет
долей деления шкалы. Винт C
служит для зажима рамки, а гайка E
– для плавной (микрометрической) ее
подачи. Части
.
В подвижной рамке укреплена вспомогательная
шкала – линейный нониус D,
с помощью которого производят отсчет
долей деления шкалы. Винт C
служит для зажима рамки, а гайка E
– для плавной (микрометрической) ее
подачи. Части
![]() обеих ножек служат для измерения
внутренних размеров тел.
обеих ножек служат для измерения
внутренних размеров тел.
Шкала нониуса
строится так, чтобы N
делений нониуса соответствовали
![]() делениям основной шкалы (k
– целое
число). Обозначим цену деления основной
шкалы через
делениям основной шкалы (k
– целое
число). Обозначим цену деления основной
шкалы через
![]() ,
цену деления нониуса через
,
цену деления нониуса через
![]() .
Тогда
.
Тогда
![]() ,
,
отсюда
![]() .
.
|
Рис. 2. Штангенциркуль |
При
![]() разность между ценой деления основной
шкалы и ценой деления нониуса равна
разность между ценой деления основной
шкалы и ценой деления нониуса равна
![]()
и
называется точностью нониуса. Точность
нониуса равна отношению цены деления
основной шкалы
к числу деления нониуса N.
Положим для определенности
![]() ,
,
![]() .
Если совместить нулевое деление шкалы
такого нониуса с нулевым делением
основной шкалы, то десятое деление
нониуса окажется совмещенным с девятым
делением основной шкалы. При этом первое
деление нониуса не дойдет до первого
деления основной шкалы на 0.1 мм, второе
деление нониуса не дойдет до второго
деления основной шкалы на 0.2 мм и т.д.
(рис. 3, а).
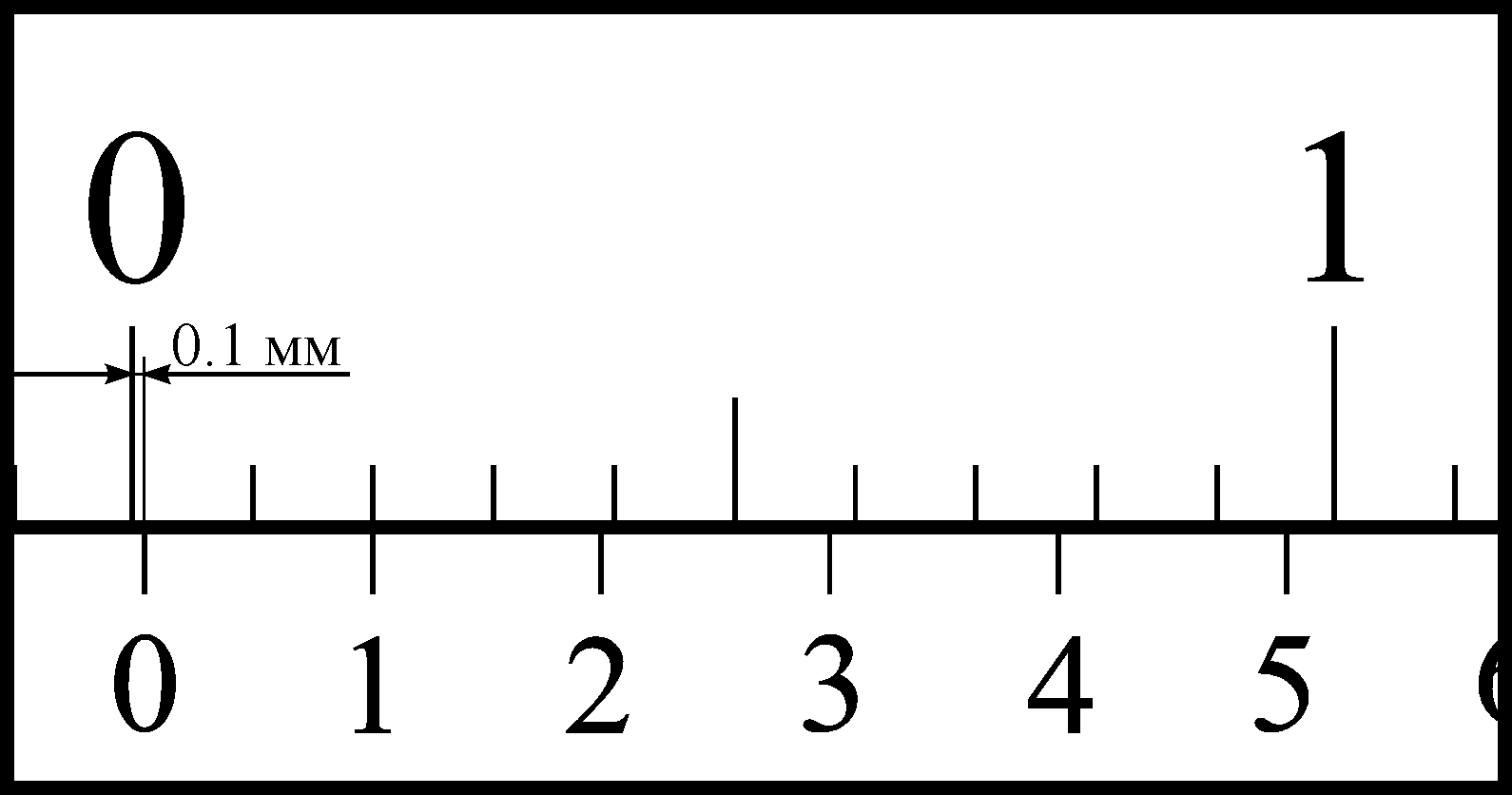
Сдвинув нониус так, чтобы его первое
деление совпало с первым делением
основной шкалы, мы создадим между
нулевыми делениями обеих шкал расстояние
0.1 мм (рис. 3, б).
.
Если совместить нулевое деление шкалы
такого нониуса с нулевым делением
основной шкалы, то десятое деление
нониуса окажется совмещенным с девятым
делением основной шкалы. При этом первое
деление нониуса не дойдет до первого
деления основной шкалы на 0.1 мм, второе
деление нониуса не дойдет до второго
деления основной шкалы на 0.2 мм и т.д.
(рис. 3, а).
Сдвинув нониус так, чтобы его первое
деление совпало с первым делением
основной шкалы, мы создадим между
нулевыми делениями обеих шкал расстояние
0.1 мм (рис. 3, б).
При совмещении
m-го
деления нониуса с
![]() делением основной шкалы нулевое деление
нониуса окажется между R
и
делением основной шкалы нулевое деление
нониуса окажется между R
и
![]() делениями основной шкалы. При этом сдвиг
нулевого деления нониуса относительно
R-го
деления основной шкалы будет составлять
m
десятых долей миллиметра.
делениями основной шкалы. При этом сдвиг
нулевого деления нониуса относительно
R-го
деления основной шкалы будет составлять
m
десятых долей миллиметра.
|
|
а |
б |
Рис. 3. Устройство нониуса |
|
Отсюда вытекает
следующее правило отсчета длины с
помощью нониуса: измеряемая длина l
равна числу целых делений основной
шкалы до нуля нониуса
![]() ,
сложенному с точностью нониуса, умноженной
на номер деления m
нониуса, совпадающего с одним из делении
основной шкалы
,
сложенному с точностью нониуса, умноженной
на номер деления m
нониуса, совпадающего с одним из делении
основной шкалы
![]() .
.
Максимальная погрешность отсчета по нониусу равна его точности.
Измеряемое тело помещают между ножками и штангенциркуля (слегка зажав ножки) и закрепляют винт С. Затем делают отсчет числа целых миллиметров по основной шкале, расположенных слева от нулевого деления нониуса, и числа деления m шкалы нониуса, совпадающего с одним из делений основной шкалы.