Порядок выполнения работы

Перед опытом необходимо через ЛАТР 9 включить вентилятор 7 и установить заданный расход воздуха ротаметром 8. Затем включить стабилизированный источник питания нагревателя калориметра 1 и наблюдать возрастание температуры на выходе калориметра (термометр 4) до достижения установившегося режима. Установившийся режим можно считать достигнутым, если с течением времени разность температур воздуха на входе и выходе из калориметра Т₂- Т_1. После достижения установившегося режима опыт проводить 10 мин., через каждые 2 мин. записывать показания термометров 4 и 5, амперметра 3. В начале и в конце опыта необходимо измерить атмосферное давление.

Рис. 1. Схема установки для определения удельной

теплоемкости воздуха

Во всех дальнейших расчетах используют средние за время опыта значения параметров, которые определяются как среднее арифметическое записанных показаний данного прибора.

По величинам, измеренным в опыте, нужно рассчитать среднюю изобарную теплоемкость воздуха С_p для интервала температур от Т₁ до Т₂. Так как нагревание производится в потоке, то расчетную формулу можно получить, учитывая, во-первых, что из-за малости тепловых потерь можно принять, что все выделенное нагревателем тепло идет на нагревание воздуха и, во-вторых, что в данной установке измеряется не массовый расход, а объемный:

, (8)

где U – напряжение на нагревателе, В; I – сила тока протекающего через нагреватель, А; Т₂ и Т₁ - температура воздуха на выходе и входе в калориметр, ⁰С; τ – время опыта, с; V₀- объемный расход воздуха через калориметр, приведенный к нормальным условиям, дм³ (Т₀=273,15 К и Р₀=760 мм. рт. ст.).

Величину V₀ можно вычислить по результатам измерений, проведенных во время опыта, в предположении, что воздух подчиняется уравнению состояния идеального газа:

, (9)

где В – атмосферное давление воздуха во время опыта, мм. рт. ст.; Т₁ - температура воздуха в лаборатории, К, определяется по термометру 4 на входе в калориметр; V – объемный расход воздуха через калориметр, дм³, определяется по показаниям газового счетчика.

Среднее для интервала температур Т₁ - Т₂ значение изобарной массовой удельной теплоемкости составит

(10)

где μ – масса моля, кг/кмоль; для воздуха μ = 28,97 кг/кмоль.

Кроме того, необходимо рассчитать и среднюю изохорную теплоемкость воздуха С_v. Так как в данном случае воздух по своим свойствам весьма близок к идеальному газу, то связь между теплоемкостями выражается формулой Майера:

,

Полученные величины изобарной и изохорной теплоемкостей следует сравнить с табличными значениями и сопоставить величину их расхождения с максимальной возможной ошибкой экспериментальных данных.

Контрольные вопросы

1. Что такое истинная и средняя теплоемкости?

2. Почему удельная изобарная теплоемкость больше удельной изохорной

теплоемкости?

3. Определение значений изобарной и изохорной теплоемкостей для идеального газа.

4. Что такое идеальный газ?

РАБОТА N2. ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ВЛАЖНОГО ВОЗДУХА

Цель работы : изучение способов определения характеристик влажного воздуха.

Основные понятия. Влажным называется воздух, в котором присутствуют водяные пары, находящиеся в перегретом или насыщенном состоянии. Основными характеристиками влажного воздуха являются абсолютная и относительная влажность, влагосодержащие, парциальное давление во водяного пара, энтальпия, температура точки росы и температура мокрого ” термометра, плотность влажного Воздуха. Абсолютная влажность - это масса водяных паров, содержащихся в 1 м³ влажного воздуха, т.е. парциальная плотность водяного пара . Рассматривая влажный воздух как смесь идеальных газов, можно зависать:

; (11)

; (12)

, (13)

где — давление влажного воздуха; , - парциальное давление водяного пара и сухого воздуха в смеси; - плотность влажного воздуха; -парциальна плотность сухого воздуха; , , - газовые постоянные водяного пара, сухого, влажного воздуха; — температура влажного воздуха , К. Парциальное давление водяного пара, находящегося в воздухе при комнатной температуре, не может быть больше давления насыщенного пара при данной температуре, так как при этом давлении пар начинает конденсироваться с выпадением капелек жидкости. Следовательно, максимальная абсолютная влажность равна плотности сухого насыщенного пара при данной температуре. Относительная влажность воздуха Φ и его массовое влагосодержание d определяются по формулам:

; (14)

(15)

где - давление сухого насыщенного пара при температуре Т.

Влагосодержание связано с парциальным давлением водяного пара соотношением

(16)

Для удобства расчетов энтальпия влажного воздуха относится к 1 кг сухого воздуха и считается равной сумме энтальпии сухого воздуха и водяного пара

, (17)

где - удельная изобарная теплоемкость сухого воздуха; - удельная теплота парообразования; - удельная изобарная теплоемкость водяного пара; - температура смеси , . В инженерных расчетах величины , и принимаются равными 1,01 кДж/(кг*^оС), 1,97 кДж/(кг*^оС), 2496 кДж/кг. Равенство (17) является приближенным, так как величина зависит от парциального давления водяного пара. На практике для расчета процессов во влажном воздухе широкое применение получила – – диаграмма. В последней по оси ординат отложены значения энтальпии влажного воздуха hвл. По оси абсцисс, которая для лучшего использования площади диаграммы проведена под углом 1З5^о к оси ординат, отложены значения влагосодержания d. Соответствующие точки спроектированы на горизонтальную (условную) ось. На диаграмме также нанесены линии постоянных температур t, постоянной относительной влажности Φ, линия парциального давления водяного пара Р_п. Шкале парциальных давлений помещена на правой ординате диаграммы.

Линия = 100 % является пограничной. В состояниях, соответствующих точкам на этой кривой, парциальное давление водяного пара и его плотность достигают максимально возможных значений при данной температуре.

Рис. 2. h - d диаграмма влажного воздуха

Применение диаграммы иллюстрирует рис. 2. Из диаграммы следует, что при охлаждения влажного воздуха (например, в процессе А - его относительная влажность возрастает. Температурой точки росы называется температура, до которой необходимо охладить воздух при постоянном влагоcодержании, чтобы его относительная влажность достигла 100 % . Температурой мокрого термометра называется температура до которой необходимо охладить воздух, при постоянной энтальпии , чтобы его относительная влажность достигла 100 % (процесс А – С на рис. 2).

Если влажность воздуха меньше 100 %, то величина t и t всегда меньше истинной температуры влажного воздуха t , часто называемой температурой «сухого» термометра и поэтому обозначаемой индексом « с ».

Для нанесения точки А на диаграмму достаточно с помощью психрометра измерить температуры «сухого» и «мокрого» термометров. Колба последнего обёрнута тканью, смоченной водой. Термометры заключены в металлические трубки, через которые с помощью вентилятора, расположенного в верхней части прибора, продувается воздух.

Газовая постоянная влажного воздуха

, (18)

где R – универсальная газовая постоянная; , - объёмные доли сухого воздуха и водяного пара

. (19)

С учётом того, что µв = 28,96, µ = 18,016, µ = 8314 кДж/(кг К), получим:

. (20)

Плотность влажного воздуха

. (21)

Порядок выполнения работы

1.Производят измерения температуры «мокрого» и «сухого» термометров.

2.С помощью h – d диаграммы определяют остальные характеристики влажного воздуха.

3.С помощью специальных таблиц, приложенных к психрометру, определяют относительную влажность φ

4.Используя таблицу теплофизических свойств насыщенного водяного пара и формулу (14), определяют парциальное давление пара.

5.По формулам (16) и (17) определяют энтальпию h_ВЛ и влагосодержание d воздуха.

6.Производят сопоставительный анализ значений, полученных с использованием формул и диаграммы.

7.Производят расчёт газовой постоянной влажного воздуха и его плотности.

Контрольные вопросы

1.Дать определение основных характеристик влажного воздуха.

2.Почему температура «мокрого» термометра отличается от температуры «точки росы»?

3.Принцип действия психрометра.

4.Методика построения h – d диаграммы.

5.Определение характеристик влажного воздуха с использованием h - d диаграммы.

6.Расчёт газовой постоянной и плотности влажного воздуха.

7.Закон Дальтона для газовой смеси.

РАБОТА №3. ИЗУЧЕНИЕ ТЕРМОДЕНАМИЧЕСКИХ ПРОЦЕССОВ В СИСТЕМЕ,СОДЕРЖАЩЕЙ НАГНЕТАТЕЛЬ ОБЪЁМНОГО ДЕЙСТВИЯ.

Цель работы: испытание и определение характеристик вакуум – насоса.

Основные понятия

Основным элементом схемы экспериментальной установки является нагнетатель, предназначенный для сжатия воздуха от давления Р1, которое ниже атмосферного давления Ро. Различие по конструкции нагнетатели газов характеризуется одинаковыми по сути термодинамическими процессами. Последние рассмотрим на примере одноступенчатого поршневого компрессора, показанного на рис. 3.

Компрессор содержит цилиндр 1, поршень 2, клапаны 3 и 4. В цилиндре 1 поршень 2 непрерывно совершает возвратно – поступательные движения. При движении поршня слева направо происходит всасывание рабочего тела (при этом клапан 3 открыт) при практически постоянном давлении. После того, как поршень дойдёт до правого крайнего положения, процесс всасывания заканчивается, клапан 3 закрывается, и поршень начинает двигаться в обратном направлении – справа налево. Давление газа в цилиндре повышается. Когда давление в цилиндре достигнет атмосферного, открывается клапан 4, и воздух поступает в атмосферу.

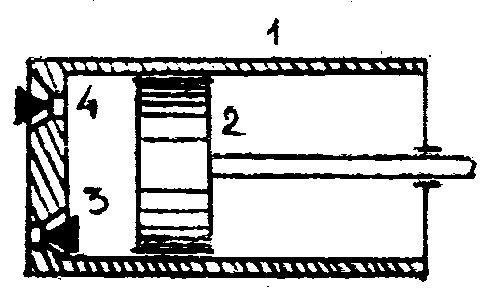
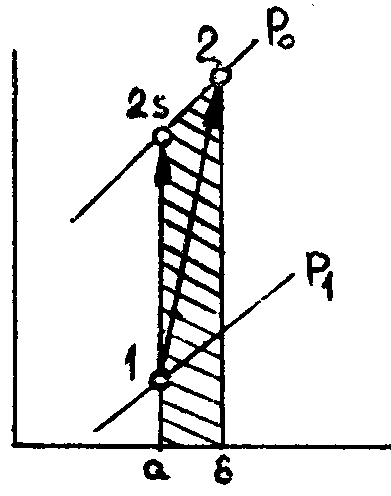Рис.3. Принципиальная схема Рис.4. Процесс сжатия

поршневого компрессора в T – S диаграмме

Техническая работа, затрачиваемая в компрессоре на сжатие воздуха за один цикл:

, (22)

где V – текущее значение объёма воздуха под поршнем при сжатии его от давления P1, до давления Ро.

Если известна массовая производительность компрессора G, то мощность, затрачиваемая на сжатие воздуха, определяется из выражения:

, (23)

где 1 – удельная работа сжатия, отнесённая к расходу, равному 1 кг/с; V – текущее значение удельного объёма воздуха, сжимаемого в компрессоре. Для идеального компрессора сжатия (процесс 1 – 2s на рис.4), осуществляемого при постоянной энтропии, величина 1 составит:

, (24)

где -показатель адиабаты, равный 1,4; -удельный объем воздуха на входе в компрессор.

Реальный процесс сжатия осуществляется с трением. Поэтому действительная работа 1_Д будет больше, чем работа 1_В в идеальном процессе. Для ее определения используют соотношение

, (25)

где – относительный КПД процесса сжатия.

Реальный адиабатный процесс сжатия 1-2 отклоняется направо от идеального процесса 1-2s. Затраты технической работы на преодоление трения будут равны площади а – 2s - 2 - б - а на рис.4.

Принципиальная схема установки

Схема установки показана на рис.5 и включает (по ходу потока воздуха) газовый счетчик 1, регулировочный вентиль 2, емкость 3, вакуумметр 4 и нагнетатель 5. Вакуум создается в емкости 3. Регулирование его величины обеспечивается вентилем 3. Основные процессы, реализуемые в установке, показаны на рис. 6 в T-S диаграмме.

С параметрами состояния ”0” воздух поступает в вентиль 2, где дросселирует до состояния ”1” . Поскольку при реализуемых в установке параметрах воздух по своим свойствам близок к идеальному газу, то можно считать, что температуре потока в точках 0 и 1 одинакова. Следовательно, можно записать

, (26)

где , – объемные расходы воздуха в точках 0 и 1 , с учетом соотношения (22), а также (23), (24).

Формула для расчета мощности, затрачиваемой на сжатие воздуха, примет вид:

, (27)

По известной удельной работе, совершаемой в процессе 1-2, можно определить температуру воздуха на выходе из рабочего объема нагнетателя

(28)

Рис.5. Принципиальная схема установки, содержащей нагнетатель объемного действия: 1- газовый счетчик; 2 – регулировочный вентиль; 3 – демфирующая емкость; 4 – вакуумметр;

5 – нагнетатель

Теплота, отводимая в нагнетателе от сжатого воздуха к элементам его конструкции и маслу (процесс охлаждения 2-3 на рис.6) составит:

, (29)

где – удельная изобарная теплоемкость воздуха; – температура воздуха на выходе из нагнетателя.

Рис.6. Основные процессы установки в T-S диаграмме

Порядок выполнения работы

1.Убедиться в исправности всей установки, проверить регулировочный вентиль, соединения в трубах.

2.Включить нагнетатель.

3. Используя вентиль 2 и вакуумметр 4, установить заданное значение вакуума.

4. Записать начальное показание счетчика, а также показание счетчика через 3 мин.

Замеры произвести при показаниях вакуумметра 0,1;0,2;0,4;0,6;0,8.

5.Определить атмосферное давление по барометру.

6.Данные измерений занести в табл.1.

Таблица 1

Величина	Номер опыта
	1	2	3	4
Показания вакуумметра М, кгс/см2 Начальное показание счетчика , дм3 Конечное показание счетчика , дм3 Время опыта, с Атмосферное давление , мм рт. ст. Остаточное давление P1, Па Производительность нагнетателя при атмосферном давлении, м3/с Объемная производительность при давлении P1, м3/с Мощность, затрачиваемая на сжатие воздуха N, кВт

7. Для каждого опыта рассчитать:

остаточное давление в ёмкости

;

объёмную производительность нагнетателя при атмосферном давлении

,

где - время проведения опыта, ; , - начальные и конечные показания счётчика, ;

объёмную производительность при остаточном давлении

;

действительную мощность , затрачиваемую на сжатие воздуха по формуле (27) при ; .

8. Результаты расчётов занесены в табл. 1 и построить графики зависимостей

;

;

.

Контрольные вопросы.

1.Определить работы сжатия в обратимых адиабатном и изотермических процессах.

2.Работы сжатия в реальном адиабатном процессе.

3.Изображение процессов сжатия в T – S диаграмме.

4.Многоступенчатое сжатие в компрессоре.

5.Выбор оптимального промежуточного давления при многоступенчатом сжатии.

6.Влияние теплоотвода на величину работы в реальном процессе сжатия.

РАБОТА №4. ИССЛЕДОВАНИЕ ИСТЕЧЕНИЯ ГАЗА ИЗ ДОЗВУКОВОГО СОПЛА

Цель работы: изучение термодинамики процесса адиабатного истечения газа из дозвукового сопла и определение его энергетических и расходных характеристик.

Основные понятия.

Дозвуковое сопло представляет собой канал, суживающийся в направлении движения потока и предназначенный для увеличения его скорости.

Ускорение потока сопровождается понижением его давления Р от начального Р₁ до конечного Р₂, равного давлению среды Р₀, в которую происходит истечение потока. Чем ниже давление Р₀, тем больше скорость газа ω на выходе из сопла. Однако в дозвуковом сопле увеличение скорости ω не может быть беспредельным и ограничено значением местной скорости звука.

Для обратимого (изотропного адиабатного) процесса истечения газа А-В (рис. 7) давление Р_2В, соответствующее условию

, (30)

равно

. (31)

Отношение давлений называется критическим перепадом давлений. При условии

справедливо равенство

. (32)

Температура потока и скорость звука при давлении определяется из выражений:

; (33)

. (34)

В реальном адиабатном процессе истечения газа часть его кинетической энергии затрачивается на преодоление трения, обусловленного вязкостью газа, шероховатостью стенок канала, неравновестностью процесса истечения и.т.д. Вследствие этого энтропия газа при его расширении возрастает и действительная адиабата отклоняется вправо от изотропы (см. рис. 7).

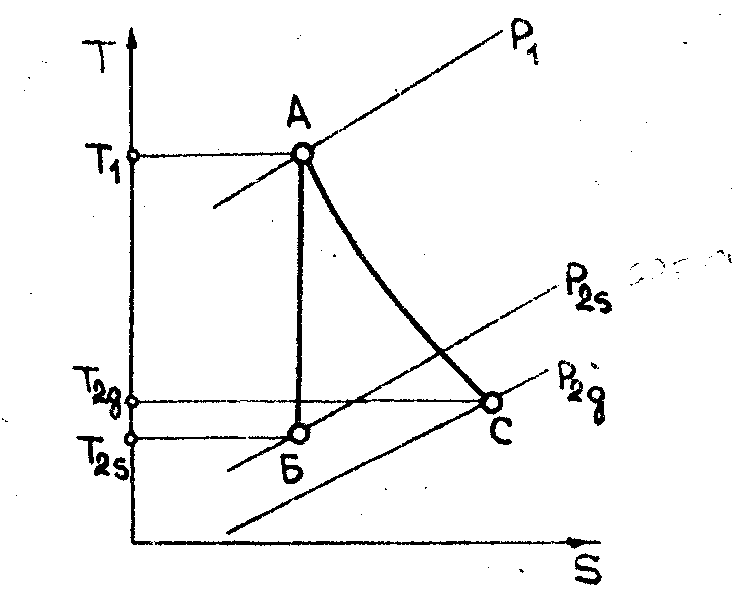
Рис. 7. Процесс расширения воздуха в суживающемся сопле:

АБ – идеальный процесс, АС – реальный процесс

Допуская, что доля энергии газа. теряемая на трение, постоянная и равна , уравнение процесса расширения запишем в виде:

, (35)

где R- газовая постоянная; - удельная изобарная теплоёмкость газа; h, V – энтальпия и объём газа; к – показатель адиабаты.

Интегрируя (35), получим уравнение, определяющее параметры газа на выходе из сопла:

. (36)

Наличие трения называется торможением потока, Поэтому его скорость ω в реальном процессе расширения до давления Р₂ всегда будет меньше скорости ω, которую имел бы поток при его обратном расширении до того же давления. Величина называется скоростным коэффициентом. Для хорошо обработанных и спрофилированных сопл, имеющих достаточно гладкую поверхность. Последний составляет 0,95…0,98.

Очевидно, что для увеличения скорости потока ω_g до максимального значения a_2g конечное давление расширения P_2g должно быть ниже значения P_2s, определяемого по формуле (29). На основе уравнения (36) для расчёта давления P₂ может быть получено следующее выражение:

. (37)

Скорость составит

. (38)

Если известно давление , то из формулы (37) следует

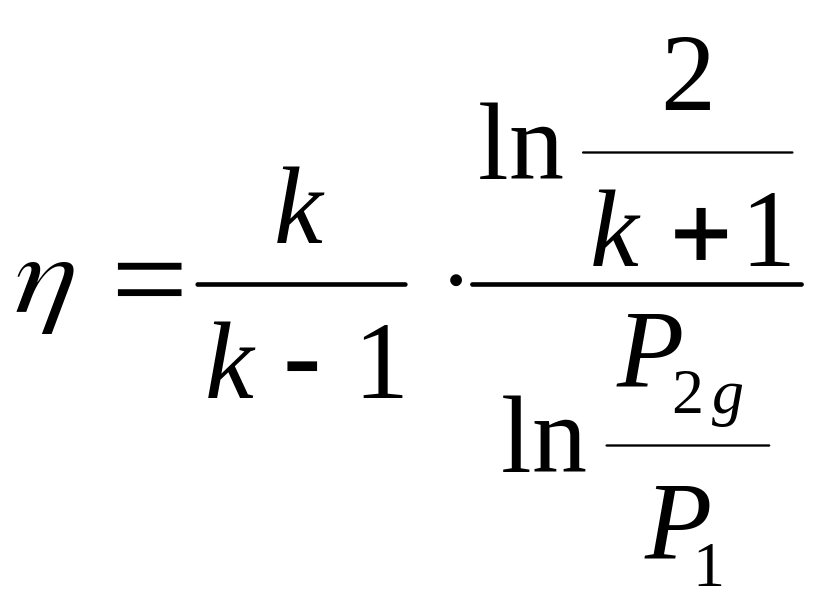. (39)

При условии величина составит

. (40)

Решая совместно уравнения (36), (37), (40), найдём:

. (41)

Снижение массового расхода газа через сопло, обусловлено наличием трения, оценивается по величине коэффициента расхода:

,

где , - расходы газа при обратимом и необратимом истечении из сопла при постоянном перепаде давлений .

При расходы и составят

, (42)

. (43)

Используя уравнения(42) и (43),нетрудно кстановить зависимость между μ и φ:

. (44)

Рис.8. Принципиальная схема установки

Принципиальная схема установки (рис.8) включает датчик давле­ния М₁, М₂, М₃ (вакуумметры), температуры Т₁ расхода G , сопла С, демпфирующую емкость Д, вакуумный насос ВН. Эскиз сопла показан на рис. 9, Демпфирующая емкость Д предназначена для установления коле­баний давления среда Р_с, в которую происходит истечение газа. Диа­метр выходного сечения сопла составляет 1,6 мм.

Порядок наполнения работы

Цель эксперимента - определение показателей η, μ, ф..

Для этого включают вакуумный насос и после достижения стационарного режима ( показания вакуумметров постоянны) определяют:

1) значения избыточного давления воздуха на срезе сопла и за соплом и ,а также барометрическое давление B;

2) абсолютные давления воздуха на срезе сопла и за соплом по формуле

где , - кгс/ см² ; В - бар;

3) по формулам (39), (41) , (44) определяют значения показателей η, μ, ф.

Рис. 9. Эскиз суживающегося сопла

Контрольные вопросы

1.Уравнение первого закона термодинамики для потока.

2.Уравнение неразрывности для потока.

3.Что такое критический перепад давления.

4.Уравнение для расчета скорости звука.

5.Характеристика реального и идеального процессов истечения.

6.Характеристика сопла Лаваля.

7.Назначение диффузоре в его профиль.

РАБОТА №5 ИЗУЧЕНИЕ ПРИНЦИПИАЛЬНОЙ СХЕМЫ И РАБОТЫ ХОЛОДИЛЬНОЙ

ПАРОКОМПРЕССОРНОЙ УСТАНОВКИ

Цель работы: знакомство о устройстаом, принципом действия холодильной установки и определение ее холодильного.

Основные понятия

Охлаждение тел до температуры, лежащей ниже температуры окружающей среды, осуществляется с помощью холодильных установок, рабо­тавших по обратному тепловому циклу. В последнем работа сжатия пре­вышает работу расширения и за счет подведенной извне работы теплота передается от нижнего источника к верхнему.

В соответствии с первым законом термодинамики

(45)

где qj - теплота, отбираемая от охлаждаемого тела;Q_Г -теплота, отводимая из холодильной установки в окружающую среду; L - работа, затрачиваемая на получение "холода".

Для характеристики термодинамической эффективности цикла холодильной установки применяется холодильный коэффициент б , определя­емый следующим образом:

(46)

Очевидно, чем больше величина ε , тем эффективность холодиль­ной установки выше.

При заданных температурах "одного" Т_Х и "горячего'' Т_Г источников наибольшую эффективность имеет обратный цикл Карно, пока­занный на рис. 10 в T – S диаграмме.

Рис.10.Обратный цикл Карно в T -S диаграмме

Рассматриваемый цикл включает следующие процессы:

(1 - 2) - изоэнтропное сжатие рабочего гола (хладоагента) в компрессоре. Начальное состояние хяадоагента характеризуется темпе­ратурой Т_Х и степенью сухости X₁ и представляет смесь паров с капельной жидкостью. На выходе из компрессора степень сухости пара равна единице, поэтому точка 2 лежит на правой пограничной кривой.

(2 - 3) - конденсация пара при постоянных температуре в давле­нии. Теплота конденсации пара отводится в окружающую среду. Состоя­ние 3 соответствует насыщенной жидкости.

(3 – 4) - изоэнтропное расширение хладоагента с совершением по­лезной работы. На выходе из расширительной машины (например, турби­ны) хладоагент находится в двухфазном состоянии. Его степень сухости X, заметно меньше, чем величина Х₁.

(4 – 1) - часть хладоагента, находящаяся в жидком состоянии, превращается в пар. Теплота, затрачиваемая на парообразование, отби­рается из охлаждаемого тела.

Для цикла Карно работа, затрачиваемая на перенос теплоты Q температурного уровня Т_Х на уровень Т_Г, составит:

, (47)

где - техническая работа, затрачиваемая на сжатие хладоаген­та в процессе (1 – 2); - техническая работа, получаемая при рас­ширении хладоагента в процессе (3 – 4).

Поскольку все процессы рассматриваемого цикла обратимы, то ра­бота L численно равна площади прямоугольника 1–2 –3–4 в T - S диаграмме, т.е.

, (48)

где s - энтропия рабочего тела в соответствующем состоянии. Величины Q_г и q_x .составят:

, . (49)

Поэтому холодильный коэффициент идеального цикла является функцией только температур Т_Г и Т_Х "горячего" и "холодного'' источников:

, (50)

Описание экспериментальной установки

На практике процессы расширения насыщенной жидкости (3-4) и сжатия влажного пара (1-4) реализовать невозможно. Поэтому цикл реальной холодильной установки по сравнению с циклом Карно имеет ряд, принципиальных отличий (рис. 11).

Рис. 11. Реальный цикл холодильной установки в

T – S диаграмме

1.Вместо процесса изоэнтропного расширения (3 – 4) (см. рис.10) с отдачей внешней работы используется процесс расширения без отдачи внешней работы (5 – 6), т.е. процесс дросселирования. В последнем энтальпия потока хладоагента не изменяется, т.е. h₅ = h₆.

2.Пар хладоагента, поступающий на сжатие в компрессор, является перегретым, т.е. его температура Т₁ выше температуры насыщения Т₇.

3.Процесс сжатия перегретого пара осуществляется с трением, поэтому указанный процесс отклоняется вправо.

4.Процесс отвода теплоты в окружающую среду включает охлажде­ние паров хладоагента при постоянном давлении от температуры Т₂ до температуры насыщения Т₃ и конденсацию пара (3 – 4) при постоянной тем­пературе, превышающей температуру теплоприемника Т_Г. Разность темпе­ратур Т₃ и Т_Г необходима для повышения интенсивности теплопередачи.

5. Для повышения интенсивности теплоотвода от охлаждаемого те­ла температура хладоагента в процессе его испарения (6 – 7 ) должна под­держиваться ниже температуры Т_Х.

6. Для предотвращения попадания жидкой фазы на вход компрессора пары хладоагента подогревают (процесс 7-1). При этом поток жидкого хладоагента перед его дросселированием охлаждают (процесс 4 – 6 ). Очевидно, что теплота, отводимая на участке 4 – 5, равна теплоте, подводимой к рабочему телу на участке

7 – 1:

. (51)

Холодильный коэффициент цикла реальной установки

, (52)

где h₁ , h₂ – энтальпии пара на входе и выходе из компрессора; h₆ , h₇ – энтальпия хладоагента на входе и выходе из испарителя; (h₂ – h₁) – удельная работа, затрачиваемая на сжатие хладоагента в компрессоре; (h₇ – h₅) – теплота, подводимая к 1 кг рабочего тела в испарителе.

Рис. 12. Принципиальная схема холодильной установки

Принципиальная схема холодильной установки , показанная на рис. 12, включает компрессор поршневого типа К_о, выполненный в одном корпусе с электродвигателем ЭД, конденсатор К, расположенный снаружи холодильника, пароперегреватель ПП, выполненный в форме двух труб малого и большого диаметров, сваренных вдоль линии касания (оси труб параллельны) , испарителя И , расположенного в верхней части холодильника, и дроссельного устройства Д, а также датчиков темпе­ратуры конденсации хладоагента в конденсаторе Т₁ и испарения в испарителе Т_2.

Порядок выполнения работы

Включить установку и после ее выхода на стационарный режим измерить:

1.С помощью микровольтметра установки – тэрмоЭДС U_и и U_к для термопар, установленных соответственно в испарителе и конденсаторе установки.

2.Температуру окружающей среды t_ОС с помощью термометра.

По измеренным величинам определяют температуру в испарителе в конденсаторе

;

,

где, Т(U) – температура, соответствующая термоЭДС U и рассчиты­ваемая по таблицам.

При условии Т_Г = Т_Х, Т_K =Т_И и по формуле (50) определя­ется холодильный коэффициент для идеальной холодильной установки.

Следующий этап работы – построение реального цикла, показанного на рис. 11 в Т – S диаграмме хладоагента R12. Указанная процедура выполняется в следующей последовательности:

1.Используя температуры Т_И и Т_К, наносят точки 4,3 и 7.

2.Определяют температуру в точке 1 по формуле

Точка 1 будет лежать на пересечении изобары , проходящей через точку 7, и изотермы с температурой T₁.

3.По известным энтропии в точке 1 и давлении в точке 3 точку 2_S и определяют энтальпию h_2S.

4.Рассчитывают энтальпию в точке 2, характеризующей состояние пара на выходе из компрессора:

,

где η_К- относительный КПД процессе сжатия, равный 0,75.

5.Определяют энтальпию точек 5 и 6, используя формулу:

.

6.Значения энтальпий, температур и давлений основных состояния хладоагента записывают в табл. 2.

Таблица 2

Параметр	Основные состояния
	1	2	3	4	5	6	7
Давление, МПа Температура, К Энтальпия, кДж/кг

Контрольные вопросы

1.Характеристика процессов обратного цикла Карно.

2.Вывод формулы для расчета холодильного коэффициента обратного цикла Карно.

3.Основные отличия реального холодильного цикла от идеального цикла.

4.Изображение реального цикла в T – S и P – h диаграммах.

5.Влияние разности температур T_X – T_И и T_К – T_Г на величину холодильного коэффициента в рельной установке.