Дробно-рациональная функция

Пусть приближающая функция ищется в виде

. (4.13)

Преобразовав равенство (4.13), получим

.

Вводя обозначения Y = 1/у, Х = 1/х, придем к линейной функции

В этом случае перед использованием формул (4.5) необходимо значения х_i, и у_i преобразовать соответственно в значения 1/х_i и 1/у_i (i = 1, ..., п). Коэффициенты a и b модели (4.13) будут равны соответственно значениям коэффициентов b и a, подсчитанным по формулам (4.5).

4.5 Способы получения математических моделей рэа

Математические модели РЭА могут быть получены аналитическим путем на основе рассмотрения физической сущности выходного параметра и математических выражений, характеризующих его поведение в тех или иных условиях. Но чаще всего математические модели получают с помощью экспериментальных исследований РЭА. При этом в практике находят применение пассивные и активные факторные эксперименты [ 10 ].

Факторными называются эксперименты, в процессе проведения которых изменяют значения первичных параметров, рассматриваемых как факторы, и фиксируют уровень выходного параметра, рассматриваемого как отклик.

Пассивным называется эксперимент, в котором изменение значений факторов достигается путем замены экземпляра устройства. Недостаток пассивного эксперимента заключается в необходимости проведения большого числа опытов.

При активном эксперименте инженер активно вмешивается в его ход путем принудительной установки (задания) в опытах нужных ему значений факторов. Активные эксперименты позволяют уменьшить количество опытов, но не всегда возможны по техническим или экономическим соображениям.

4.6 Применение пассивного эксперимента для получения

математических моделей

Рассмотрим основные этапы процедуры получения математических моделей РЭА с использованием пассивных экспериментов:

1. Для рассматриваемого вида устройства выявляются первичные параметры (факторы), в наибольшей степени влияющие на выходной параметр. Число этих факторов k рекомендуется ограничивать значением k  5 ... 8;

2. Определяется требуемое количество опытов пассивного эксперимента п или, что то же самое, требуемое число замен экземпляра устройства:

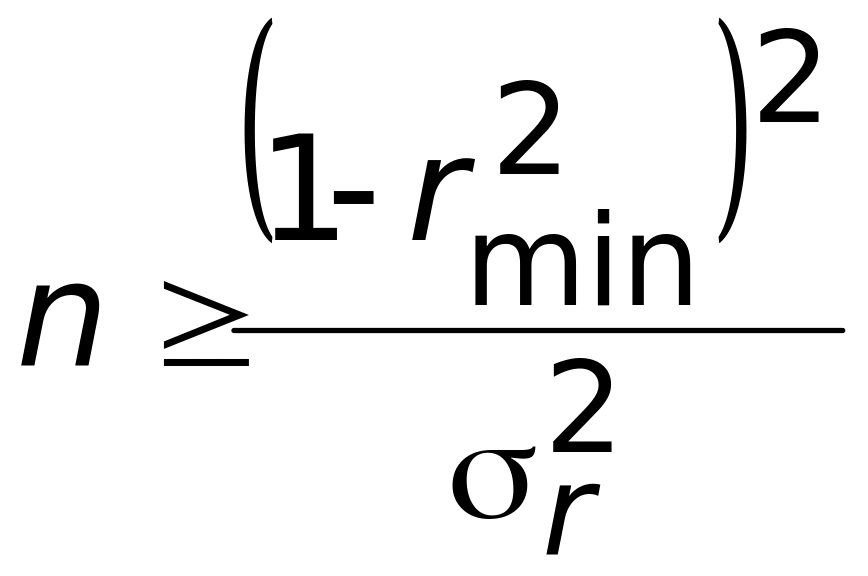, (4.14)

где r_min — минимальное значение коэффициента парной корреляции между первичным параметром (фактором) и выходным параметром, считаемое еще значимым (существенным, весомым); обычно  — среднее квадратическое отклонение коэффициента корреляции. Значение определяют, как

, (4.15)

где t_ — коэффициент, зависящий от доверительной вероятности  (таблица 4.1).

Таблица 4.1— Значение коэффициента в зависимости от вероятности 

	0,8	0,85	0,9	0,95	0,99	0,9973	0,999
t	1,282	1,439	1,643	1,960	2,576	3,000	3,290

Пример. Требуется определить, какое число опытов пас­сивного эксперимента необходимо провести для случая, когда принято значение . Доверительная вероятность  =0,95.

Решение. По таблице 4.1 для  = 0,95 находим t_ = 1,96. По формуле (4.15) вычислим значение _r:

.

Используя выражение (4.14), определим требуемое число опытов:

.

Нетрудно убедиться, что для  = 0,2 число опытов п   89;

3. Проводятся опыты пассивного эксперимента. Проведение опытов включает:

— наблюдение (измерение) значений факторов для исследуемого экземпляра устройства;

— регистрацию (измерение) значения выходного параметра, соответствующего наблюдаемым значениям факторов;

— замену экземпляра устройства.

Результаты опытов рекомендуется сводить в таблицу 4.2

Таблица 4.2— Рекомендуемая форма записи результатов пассивного эксперимента

Номер опыта (экземпляр устройсва)	Значение фактора			Уровень выходного параметра у
	x1	...	xk
1
...
n

4. Выполняется статистическая обработка результатов опытов. В общем случае сложность математической обработки зависит от того, коррелированны ли между собой факторы. Статистическая обработка в настоящее время, как правило, выполняется на ЭВМ с использованием библиотечных программ. По результатам статистической обработки строят модели в виде уравнения регрессии. Часто вначале строят линейную модель

, (4.16)

где у — выходной параметр; — факторы; k — количество факторов, принятых во внимание; — коэффициенты модели, получаемые из эксперимента.

При записи математической модели в нее включают только значимые коэффициенты. Проверка значимости, как правило, является составной частью статистической обработки и выполняется с помощью тех же библиотечных программ. Проверить значимость коэффициента модели означает дать ответ на вопрос, за счет чего коэффициент оказался отличным от нуля — за счет случайных причин (ограниченного числа опытов), либо за счет того, что это объективно имеет место.

Процедура проверки значимости, реализует обычно следующий алгоритм.

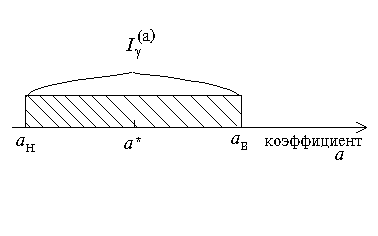
Рисунок 4.4 — Доверительный

интервал для коэффициента a:

1. Для рассматриваемого коэффициента, например а, определяется доверительный интервал (интервальная оценка) , соответствующий доверительной вероятности :

где — границы интервала;

2. Далее уточняется вопрос, попадает ли в построенный доверительный интервал точка а = 0 (рисунок 4.4), (а^* — точечная оценка).

Если это происходит, то нет оснований точечную оценку а^*, полученную при статистической обработке, считать значимой, так как отличной от нуля она могла оказаться за счет ограниченности числа опытов, погрешностей эксперимента и других случайных причин. Следовательно, такой коэффициент (слагаемое с коэффициентом а^*) не следует включать в формируемую математическую модель.

Если в дальнейшем выяснится, что линейная модель вида (4.16) окажется неадекватной результатам эксперимента, то с использованием библиотечных программ для ЭВМ, строят математическую модель в виде степенного полинома. Обычно ограничиваются полиномом второй, реже третьей степени;

3. Проверяется пригодность построенной модели для целей практики. Об этом судят по ее адекватности результатам эксперимента.

Проверить адекватность модели означает выяснить вопрос, за счет чего имеют место расхождения между значениями выходного параметра, полученными экспериментально и подсчитанными по построенной математической модели, — за счет погрешностей в опытах, либо за счет того, что модель плохо описывает поведение выходного параметра РЭА. Многие библиотечные программы при проверке адекватности используют критерий Фишера.