5.2. Языки описания цифровых автоматов

В зависимости от задания функций переходов и выходов ( и ) в настоящее время выделяют два класса языков – начальные языки и стандартные или автоматные языки. В начальных языках автомат описывается на поведенческом уровне, т.е. функции переходов и выходов обычно в явном виде не задаются. Функционирование автомата описывается в терминах входных и выходных последовательностей, реализуемых операторов или управляющих последовательностей сигналов, воздействующих на операционный автомат. В автоматных языках функционирование автомата задается путем явного задания функций переходов и выходов.

Начальные языки. Среди начальных языков следует выделить язык регулярных выражений алгебры событий, язык логических схем алгоритмов, язык граф-схем алгоритмов.

Язык регулярных выражений алгебры событий. Для заданного конечного множества входных букв при построении регулярного выражения используются три операции над событиями (две бинарные и одна унарная):

1. - объединение (дизъюнкция);

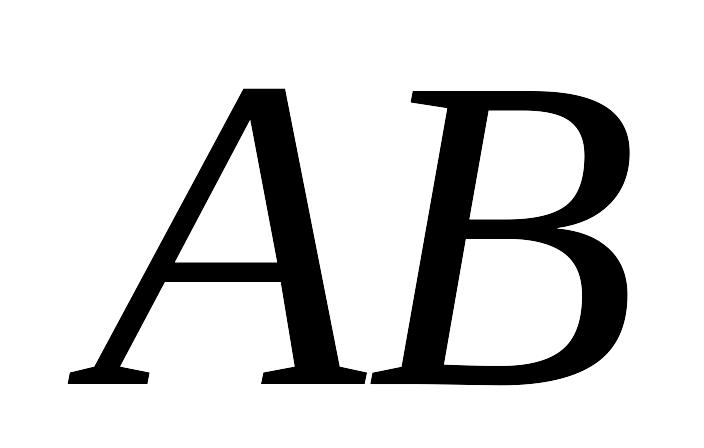2. - умножение (конкатенация);

3. - итерация (обозначается также А^*).

Выражение, построенное из букв алфавита X и из символов операций объединения, умножения и итерации с использованием соответствующим образом круглых скобок, называется регулярным выражением в алфавите X. Всякое регулярное выражение R определяет некоторое событие S. Регулярным событием S называется событие, полученное из элементарных событий (однобуквенных слов ) применением конечного числа раз операций дизъюнкции, умножения и итерации.

Пусть необходимо описать автомат, выдающий сигнал всякий раз, когда происходит изменение входной буквы с на , т.е. сигнал должен выдаваться в ответ на любые входные последовательности, кончающиеся последовательностью . Такое событие записывается как ( ). Тогда событие , в ответ на которое должен выдаваться сигнал , будет описываться регулярным выражением: .

Язык логических схем алгоритмов. В 1953 г. А.А. Ляпунов предложил записывать алгоритмы в виде конечной строчки, состоящей из символов операторов, логических условий и верхних и нижних стрелок, которым приписаны натуральные числа.

Выполненная таким образом запись алгоритма называется логической схемой алгоритма (ЛСА).

Логические схемы алгоритмов удовлетворяют следующим условиям:

1. содержат один начальный ( 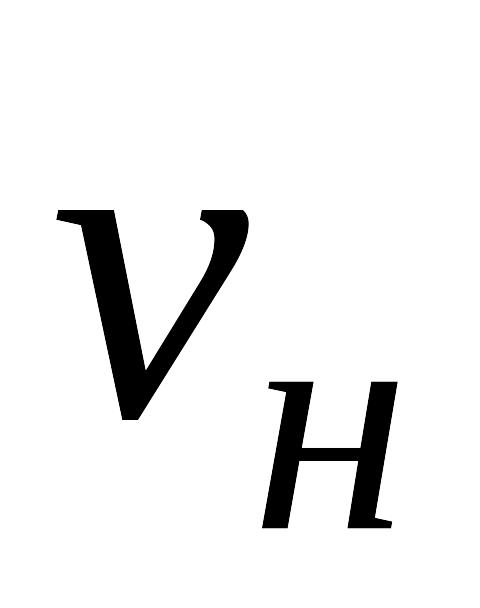)и один конечный ( 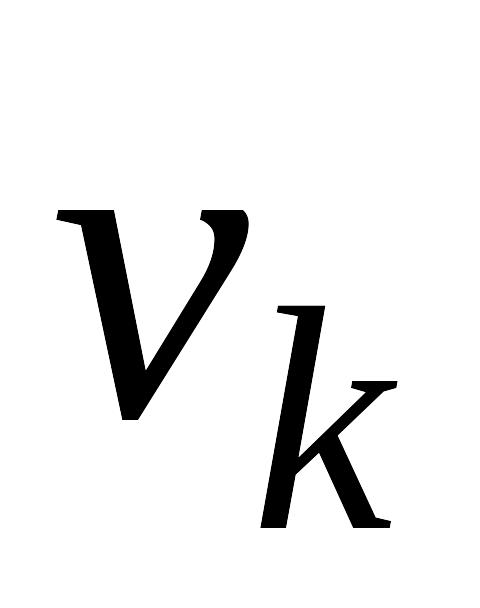) оператор;

2. перед оператором и после оператора стрелок быть не должно;

3. вслед за каждым логическим условием стоит верхняя стрелка;

4. не существует двух одинаковых (с одинаковыми цифрами) нижних стрелок;

5. для каждой нижней стрелки должна быть, по крайней мере, одна соответствующая ей (с одинаковой цифрой) верхняя стрелка;

6. для каждой верхней стрелки должна быть точно одна соответствующая ей (с одинаковой цифрой) нижняя стрелка.

Описание функционирования автомата с помощью ЛСА рассмотрим на следующем примере:

(5.4)

Эта ЛСА имеет оператора начала и конца ( и ), пять операторов ( ) и три логических условия ( ). Начальному оператору соответствует некоторое начальное состояние автомата, при котором никакие микрооперации не выполняются. Если в начальном состоянии на первый вход устройства придет сигнал, равный единице ( ), то устройство перейдет в новое состояние, в котором выполняется оператор - первый справа после логического условия , а затем проверяется логическое условие .

Если же , то выходим по верхней стрелке  и входим по нижней стрелке с той же цифрой на проверку условия , минуя выполнения оператора .

Если , то переходим к выполнению оператора . Если же , то выполняются операторы и и проверяется условие . Если , то оператор не выполняется, происходит переход к оператору . После выполнения оператора происходит переход к конечному оператору, т.е. работа дискретного устройства заканчивается.

Язык граф-схем алгоритмов. Граф-схема алгоритма – ориентированный связный граф, содержащий одну начальную вершину, произвольное число условных и операторных вершин и одну конечную вершину.

Конечная, операторная и условная вершины имеют по одному входу, начальная вершина входов не имеет, условная вершина имеет два выхода, помеченных символами 1 и 0.

Граф-схема алгоритма удовлетворяет следующим условиям:

1. входы и выходы вершин соединяют друг с другом с помощью линий, направленных всегда от выхода ко входу;

2. каждый выход соединен только с одним входом;

3. любой вход соединяется, по крайней мере, с одним выходом;

4. любая вершина графа лежит, по крайней мере, на одном пути из начальной к конечной вершине;

5. в каждой условной вершине записывается один из элементов множества логических условий 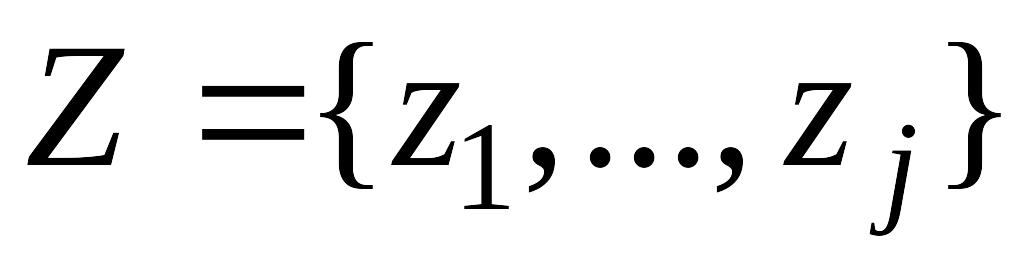, разрешается в различных условных вершинах запись одинаковых элементов множества Z;

6. в каждой операторной вершине записывается один из элементов множества операторов 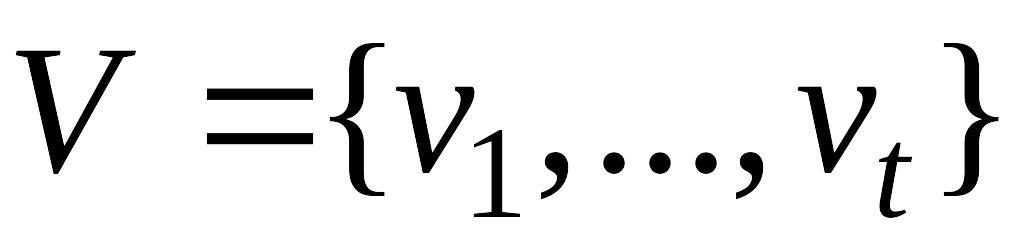, разрешается в различных операторных вершинах запись одинаковых элементов множества V.

На рис. 5.3 представлен граф-схема алгоритма, описанного выражением (5.4).

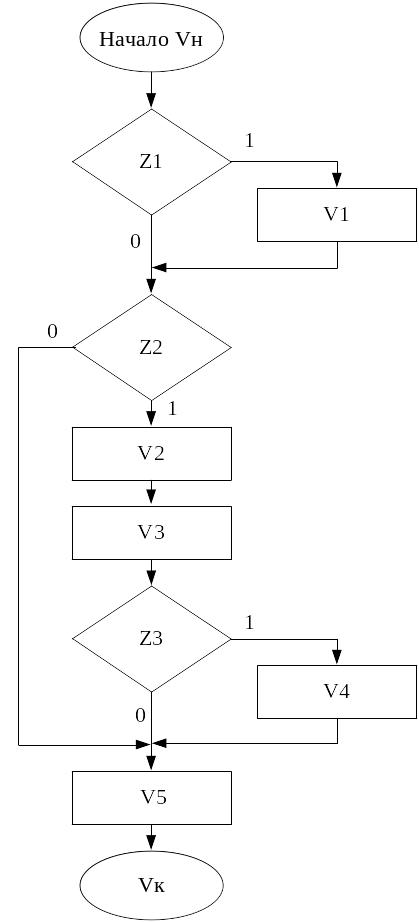
Рисунок 5.3 Граф схема алгоритма

Язык ГСА используется очень часто при описании алгоритмов функционирования, как самого цифрового автомата, так и программ, выполняющих то, или иное действие.

Автоматные языки. Среди автоматных языков наиболее распространены таблицы, графы и матрицы переходов и выходов.

Таблица переходов (выходов) представляет собой таблицу с двойным входом, строки которой пронумерованы входными буквами, а столбцы - состояниями. На пересечении указывается состояние, в которое переходит автомат (в таблице переходов) или выходной сигнал, выдаваемый им (в таблице выходов).

Описание работы автомата Мили таблицами переходов и выходов показано в табл.5.1 и 5.2 соответственно.

Таблица 5.1 Таблица переходов Таблица 5.2. Таблица выходов

Входной сигнал	Состояние автомата				Входной сигнал	Состояние автомата

На пересечении столбца и строки в таблице переходов ставится состояние , в которое автомат переходит из состояния под действием сигнала , а в таблице выходов соответствующий этому переходу выходной сигнал

Иногда при задании автомата Мили используют одну совмещенную таблицу переходов и выходов, в которой на пересечении столбца и строки записывают в виде следующее состояние и выдаваемый выходной сигнал. Совмещенная таблица имеет вид (табл.5.3)

Таблица 5.3. Совмещенная таблица переходов и выходов

Входной сигнал	Состояние автомата

Часто автомат задают с помощью графа автомата. Этот язык удобен и нагляден. Граф автомата - ориентированный граф, вершины которого соответствуют состояниям, а дуги переходам между ними. Две вершины графа автомата и (исходное состояние и состояние перехода) соединяются дугой, направленной от к , если в автомате есть переход из в , т.е. если при некотором . Дуге ( , ) графа автомата приписывается входной сигнал и выходной сигнал . На рис.5.4 приведен граф автомата, описанный табличным способом.

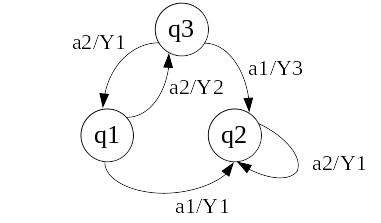
Рисунок 5.4. Граф автомата Мили