
- •1. Представление числовой информации в цифровых автоматах
- •1.1. Выбор системы счисления для представления числовой информации
- •1.2. Представление отрицательных чисел
- •1.3. Формы представления чисел
- •2. Арифметические основы цифровых автоматов
- •2.1. Формальные правила сложения и вычитания двоичных чисел
- •2.2. Сложение чисел, представленных в форме с фиксированной запятой
- •2.3.Переполнение разрядной сетки
- •2.4. Сложение чисел, представленных в форме с плавающей запятой
- •3. Умножение двоичных чисел
- •3.1. Методы умножения двоичных чисел
- •3.2. Умножение чисел, представленных в форме с фиксированной запятой в прямом коде
- •3.3. Умножение чисел, представленных в форме с фиксированной запятой в дополнительном коде
- •3.4. Умножение чисел, представленных в форме с фиксированной запятой в обратном коде
- •3.5. Умножение чисел, представленных в форме с плавающей запятой
- •3.6. Ускорение операции умножения
- •5. Цифровые автоматы
- •5.1. Основные понятия
- •5.2. Языки описания цифровых автоматов
- •5.3 Проектирование конечных автоматов
3. Умножение двоичных чисел
3.1. Методы умножения двоичных чисел
Применительно к двоичной системе счисления наиболее известны следующие основные способы выполнения операции умножения:
1) умножение, начиная с младших разрядов множителя:

2) умножение, начиная со старших разрядов множителя:

В обоих случаях операция умножения состоит из ряда последовательных операций сложения частичных произведений. Операциями сложения управляют разряды множителя: если в каком-то разряде множителя находится единица, то к сумме частичных произведений добавляется множимое с соответствующим сдвигом; если в разряде множителя – нуль, то множимое не прибавляется.
Таким образом, кроме операции сложения чисел для получения произведения необходима операция сдвига чисел. При этом появляется возможность сдвигать множимое или сумму частичных произведений, что дает основание для разных методов реализации операции умножения.
Метод 1. Умножение, начиная со старшего разряда и сдвигом множимого вправо.

Метод 2. Умножение, начиная с младшего разряда и сдвигом суммы частичных произведений вправо.
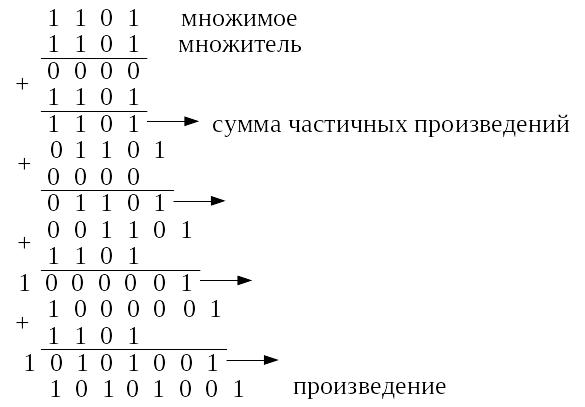
Метод 3. Умножение, начиная с младшего разряда и сдвигом множимого влево.

Метод 4. Умножение, начиная со старшего разряда и сдвигом суммы частичных произведений влево.

3.2. Умножение чисел, представленных в форме с фиксированной запятой в прямом коде
Пусть заданы машинные изображения чисел:
![]()
Тогда их произведение:
![]() ,
,
где
![]() .
.
Пример 3.1. Умножить число
![]() и
и
![]() .
.
Решение. Знак произведения определим отдельно от цифровой части:
![]() .
Цифровую часть определим, используя
метод умножения 2.
.
Цифровую часть определим, используя
метод умножения 2.

Если получится единица переноса из
старшего разряда, то ее нужно сохранить.
В результате получим:
![]() ,
а
,
а
![]() .
.
3.3. Умножение чисел, представленных в форме с фиксированной запятой в дополнительном коде
В случае, когда числа в машине хранятся в дополнительном коде целесообразно все операции над числами производить в дополнительном коде. Однако при этом возникает ряд особенностей, которые необходимо учитывать.
Произведение дополнительных кодов сомножителей равно дополнительному коду результата только в случае положительного множителя, при этом используются модифицированные коды.
Пример 3.2. Умножить числа
![]() и
и
![]() в дополнительных кодах.
в дополнительных кодах.
Решение. Запишем машинные изображения чисел A и B в модифицированном дополнительном коде.
![]()
![]()
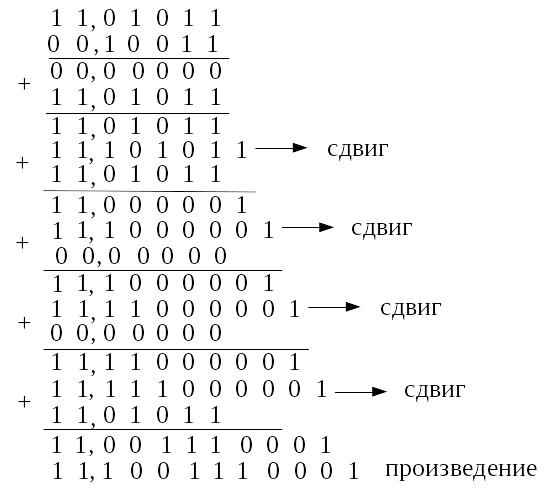
Таким образом
![]() ,
а
,
а
![]() .
.
Если множитель отрицательное число, то
произведение чисел в дополнительном
коде получается прибавлением поправки
![]() к произведению дополнительных кодов
сомножителей.
к произведению дополнительных кодов
сомножителей.
Пример 3.3. Умножить числа
![]() и
и
![]() в дополнительных кодах.
в дополнительных кодах.
Решение. Запишем машинные изображения чисел A и B в модифицированном дополнительном коде.
![]()
![]()
![]()
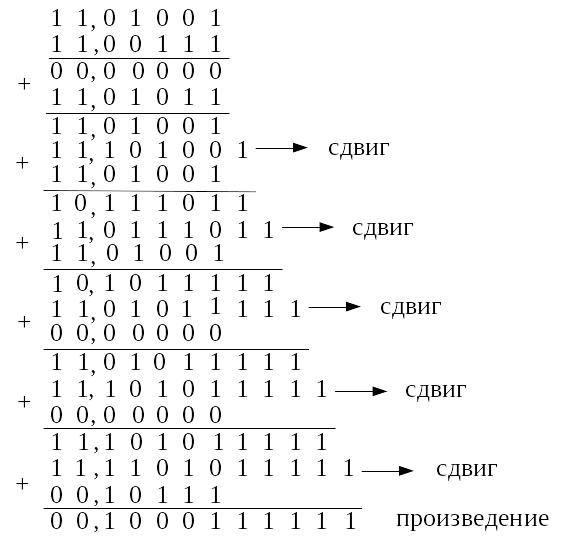
Таким образом
![]() .
.
3.4. Умножение чисел, представленных в форме с фиксированной запятой в обратном коде
Произведение обратных кодов сомножителей
равно обратному коду результата только
в случае положительного множителя. Если
множитель – отрицательное число, то
произведение чисел в обратном коде
получается прибавлением
![]() к произведению обратных кодов сомножителей.
к произведению обратных кодов сомножителей.
Пример 3.4. Умножить числа
![]() и
и
![]() в обратном коде.
в обратном коде.
Решение. Запишем машинные изображения чисел A и B в модифицированном обратном коде.
![]()
![]()
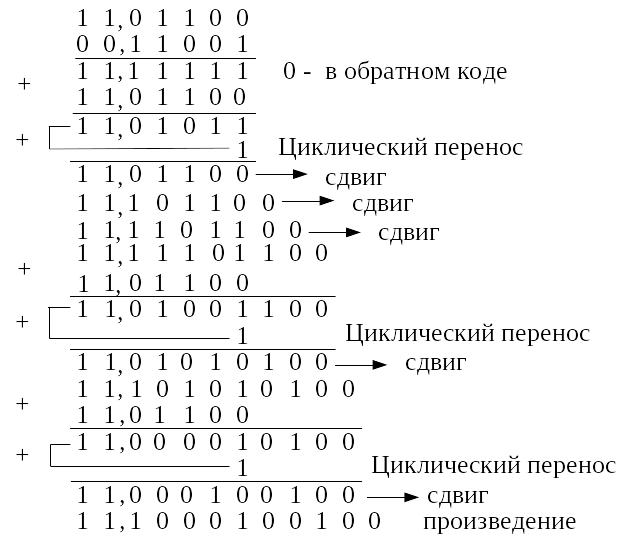
Таким образом,
![]() ,
а
,
а
![]()
Пример 3.5. Умножить числа и .
Решение. Запишем машинные изображения чисел A и B в модифицированном обратном коде.
![]()
![]()
![]()

![]()
