
РОСЖЕЛДОР
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Ростовский государственный университет путей сообщения»
(ФГБОУ ВПО РГУПС)

Кафедра «Связь на железнодорожном транспорте»
В.М. ПАВЛОВ
РАСЧЕТ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ В ВОЛНОВОДЕ
Учебно-методическое пособие для выполнения курсовой работы
по дисциплине «Электромагнитные поля и волны»
Ростов-на-Дону
2012
УДК 621.372.8 (07)
Павлов В.М.
Расчет электромагнитного поля в волноводе. Методическое пособие для выполнения курсовой работы по дисциплине «Электромагнитные поля и волны».
Пособие предназначено для студентов факультета АТС. Содержащиеся в пособии теоретические сведения и методические указания позволяют более рационально и продуктивно использовать время, отводимое для выполнения курсовой работы по дисциплине «Электромагнитные поля и волны». Кроме того, пособие может быть использовано студентами других факультетов, изучающих родственные дисциплины.
Рис. 3. Табл. 1. Библ. наим. 3
![]() Павлов
В.М., 2012
Павлов
В.М., 2012
Оглавление
1 Краткие сведения из теории..................................................................................
1.1 Прямоугольный волновод........................................................................
1.2 Поперечно-электрические поля...............................................................
1.3 Поперечно-магнитные поля.....................................................................
1.4 Поверхностные токи в волноводе...........................................................
2 Задание на курсовую работу.................................................................................
3 Методические указания.........................................................................................
4 Список использованных источников...................................................................
Приложение А Некоторые сведения из векторного анализа
Приложение Б Структура электромагнитных полей в прямоугольном волноводе
Приложение В Варианты заданий и исходные данные
Приложение Г Образец оформления титульного листа
Приложение Д Образец оформления задания
Введение
Направляющими
системами в электродинамике называются
технические устройства, которые
принудительно направляют (канализируют)
поток энергии переменного электромагнитного
поля в нужном направлении (например, от
передатчика к антенне или от антенны к
приемнику). В начале развития радиотехники,
которая за время своего существования
продвинулась в направлении возрастания
практически используемых частот от
![]() Гц до
Гц до
![]() Гц, направляющие системы были представлены
открытыми двух -, трех -, четырех -
проводными линиями, широко применяемыми
и в настоящее время.
Гц, направляющие системы были представлены
открытыми двух -, трех -, четырех -
проводными линиями, широко применяемыми
и в настоящее время.
При повышении частоты многопроводные линии, будучи открытыми, перестали справляться с возложенной на них задачей: передачей энергии электромагнитного поля с малыми потерями.
На коротких волнах, сравнимых с размерами открытой линии, последние заметную часть энергии начинают излучать в поперечном направлении. С укорочением длины волны приходится уменьшать поперечные размеры линии (только при этом условии она нормально работает как устройство передачи - длинная линия). Поперечное излучение эффективно устраняется введением экрана.
Однако, в высокочастотной радиоэлектронике такие линии не нашли широкого применения: конструкция их сложна, вдобавок трудно поддержать постоянным на большой длине линии соотношение поперечных размеров и форму сечения. Тем не менее, двухпроводные линии и сегодня еще применяются для передачи энергии электромагнитных волн длиной вплоть до метрового диапазона. На дециметровых волнах двухпроводные линии пришлось полностью заменить коаксиальными линиями передачи.
В коаксиальной линии вся энергия передается в пространстве между центральным и внешним проводниками, и потери на излучение в поперечном направлении исключены. Однако по мере приближения к сантиметровым волнам и в коаксиальной линии стали проявляться недостатки: с ростом частоты, то есть с укорочением длины волны, приходится пропорционально уменьшать поперечные размеры линии, при этом выдержать постоянными радиусы внутреннего и внешнего проводников, их соосность становится трудно. Возникающие неизбежные отклонения поперечных размеров нарушают нормальный режим распространения волн в такой линии.
Другой недостаток связан с опасностью электрического пробоя, который возникает в месте высокой концентрации электрического поля у поверхности внутреннего проводника. Плотность тока, протекающего по поверхности внутреннего проводника, больше, чем по поверхности внешнего. Поэтому потери коаксиальной линии, связанные со скин-эффектом, в наибольшей степени вызваны наличием именно внутреннего проводника.
В сантиметровом диапазоне волн на смену коаксиальным линиям пришли полые металлические трубы, в которых внутренний проводник удален.
Полые металлические волноводы перекрывают весь сантиметровый и длинноволновую часть миллиметрового диапазонов.
1 Краткие сведения из теории
1.1 Прямоугольный волновод
В диапазоне сверхвысоких частот (СВЧ) широко применяются радиоволноводы или просто - волноводы. Волновод представляет собой полую металлическую трубу, в которой при определенных условиях могут распространяться электромагнитные волны.
Для определения поля в полом волноводе в общем случае необходимо решить систему уравнений Максвелла или соответствующих им волновых уравнений. При этом решение ищут в той системе координат, координатные поверхности которой по форме подобны внутренней поверхности волновода, т.е. решение уравнений Максвелла для прямоугольного волновода ищут в прямоугольной системе координат, для круглого - в цилиндрической. Постоянные интегрирования находят исходя из требования, чтобы полученные решения удовлетворяли граничным условиям на внутренней поверхности волновода.
Рассмотрим свойства наиболее распространенного типа волноводов: прямоугольного (рисунок 1) [1,2].
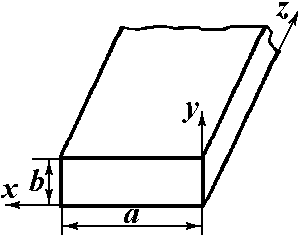
Рисунок 1
Для исследования структуры электромагнитного поля в волноводе, необходимо решить уравнения Максвелла в комплексной форме
![]() ,
,
![]() , (1)
, (1)
в области
![]() ;
;
![]() ;
;
![]() (2)
(2)
при заданных граничных условиях на проводящих стенках волновода:
![]() при
при
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
. (3)
;
. (3)
В выражениях (1) и
далее
![]() - мнимая единица.
- мнимая единица.
В дальнейших
выражениях индекс "![]() "
у комплексных амплитуд опустим.
"
у комплексных амплитуд опустим.
Параметры среды,
заполняющей внутреннее пространство
волновода
![]() ,
,
![]() ,
,
![]() ,
,
где ![]() [Ф/м] - абсолютная диэлектрическая
проницаемость среды;
[Ф/м] - абсолютная диэлектрическая
проницаемость среды;
![]() - относительная
диэлектрическая проницаемость среды;
- относительная
диэлектрическая проницаемость среды;
![]() [Ф/м] - абсолютная
диэлектрическая проницаемость вакуума;
[Ф/м] - абсолютная
диэлектрическая проницаемость вакуума;
![]() [Гн/м] - абсолютная
магнитная проницаемость среды;
[Гн/м] - абсолютная
магнитная проницаемость среды;
![]() - относительная
магнитная проницаемость среды;
- относительная
магнитная проницаемость среды;
![]() [Гн/м] - абсолютная
магнитная проницаемость вакуума;
[Гн/м] - абсолютная
магнитная проницаемость вакуума;
![]() [Ом]-
волновое сопротивление среды.
[Ом]-
волновое сопротивление среды.
Будем считать, что
волновод имеет большую протяженность,
и что источники поля в рассматриваемой
области отсутствуют. Нас будут интересовать
условия, при которых решение уравнений
поля имеет форму бегущей волны,
распространяющейся вдоль оси волновода
в направлении возрастающих значений
![]() .
Поэтому
положим, что зависимость всех составляющих
поля
.
Поэтому
положим, что зависимость всех составляющих
поля
![]() и
и
![]() от координаты
имеет вид
от координаты
имеет вид
![]() , (4)
, (4)
где
![]() - постоянная
распространения, которая должна быть
найдена в результате решения уравнений
Максвелла при граничных условиях (3).
- постоянная
распространения, которая должна быть
найдена в результате решения уравнений
Максвелла при граничных условиях (3).
Условие (4) означает,
что дифференцирование комплексных
амплитуд любой из проекций вектора
![]() или
или
![]() по переменной
эквивалентно
умножению этой проекции на
по переменной
эквивалентно
умножению этой проекции на
![]() ,
т.е. оператор
,
т.е. оператор
![]() .
.
Из уравнений Максвелла (1) в декартовой системе координат (приложение А) для внутреннего пространства волновода получим:
![]() , (5)
, (5)
![]() , (6)
, (6)
![]() , (7)
, (7)
![]() , (8)
, (8)
![]() , (9)
, (9)
![]() . (10)
. (10)
Проведем
преобразование системы уравнений (5) -
(10) так, чтобы выразить поперечные
составляющие векторов (![]() ,
,![]() ,
,![]() ,
,![]() )
через продольные
)
через продольные
![]() и
и
![]() .
Для этого в уравнения (5) и (6) подставим
значения
и
из
уравнений (8) и (9) и после простых
преобразований получим:
.
Для этого в уравнения (5) и (6) подставим
значения
и
из
уравнений (8) и (9) и после простых
преобразований получим:
![]() , (11)
, (11)
![]() , (12)
, (12)
где
![]() - поперечное волновое число,
- поперечное волновое число,
![]() ,
- волновое число,
,
- волновое число,
![]() - скорость волны
в среде, заполняющей волновод,
- скорость волны
в среде, заполняющей волновод,
![]() - длина волны в
этой среде.
- длина волны в
этой среде.
Теперь,
подставляя в уравнения (8) и (9) значения
![]() ,
и
,
и
![]() из
уравнений (5) и (6), получим уравнения для
составляющих
из
уравнений (5) и (6), получим уравнения для
составляющих
![]() и
и
![]() ,
выраженных через величины
и
.
,
выраженных через величины
и
.
![]() , (13)
, (13)
![]() . (14)
. (14)
Таким образом, все
составляющие векторов
![]() и
и
![]() ,
касательные к плоскости поперечного
сечения (поперечные составляющие),
определяются через продольные составляющие
и
.
Уравнения для продольных составляющих
легко получить, подставляя значения
и
из (11) и (12) в
уравнение (10), а значения
и
из (13) и (14) в уравнение (7), тогда
,
касательные к плоскости поперечного
сечения (поперечные составляющие),
определяются через продольные составляющие
и
.
Уравнения для продольных составляющих
легко получить, подставляя значения
и
из (11) и (12) в
уравнение (10), а значения
и
из (13) и (14) в уравнение (7), тогда
![]() , (15)
, (15)
![]() . (16)
. (16)
Это волновые уравнения [3].
Из
выражений (11)
- (14) следует,
что электромагнитное поле в прямоугольном
волноводе в общем случае представляет
собой
сумму двух независимых частных полей,
одно из которых называется
поперечно-электрическим (![]() полем или
полем или
![]() полем).
полем).
![]() ;
; ![]() ;
; ![]() , (17)
, (17)
![]() ;
; ![]() ;
; ![]() , (18)
, (18)
так
как не содержит продольных составляющих
электрического поля
![]() .
.
Второе
получило название поперечно-магнитное
(или
![]() поле,
поле,
![]() поле)
поле)
![]() ;
; ![]() ;
; ![]() , (19)
, (19)
![]() ;
; ![]() ;
; ![]() . (20)
. (20)
так как не содержит
продольных составляющих магнитного
поля
![]() .
.
Перейдем к рассмотрению каждого из этих полей.
