Занятие 3 Законы сохранения импульса, момента импульса и механической энергии

Исходя из закона изменения импульса (2.1), можно рассмотреть частный случай, когда сумма внешних сил равна нулю. Тогда импульс системы не изменяется во времени (закон сохранения импульса):

(3.1)

Исходя из закона изменения момента импульса (2.3), можно рассмотреть частный случай, когда сумма внешних моментов сил равна нулю. Тогда момент импульс системы не изменяется во времени (закон сохранения момента импульса):

(3.2)

Очень часто в физических задачах рассматривается модель очень краткого взаимодействия двух или нескольких тел (столкновение двух тел в полете, взрыв сняряда и разлет осколков, столкновение свободного тела с телом, подвешенным на шарнире, и т.д.). Если в таких ситуациях результирующая сила или момент сил за время столкновения не существенно изменяют импульс (2.2) или момент импульса (2.4), то законы (3.1) и (3.2) можно считать почти точными.

В случаях существенного изменения импульса или момента импульса остается возможность применения законов сохранения (3.1) и (3.2) только в проекции на ось, проекция результирующей силы или момента силы на которую равны нулю:

(3.3)

(3.4)

Третьим основным законом механики является закон изменения полной механической энергии системы , где – потенциальная энергия системы тел, – кинетическая энергия этой системы:

, (3.5)

где – работа неконсервативных сил.

Если работа неконсервативных сил равна нулю, то выполняется закон сохранения механической энергии:

(3.6)

В механических задачах чаще всего учитываются два типа потенциальных энергий и два типа кинетических.

Гравитационная потенциальная энергия и потенциальная энергия упругой деформации

или (3.7)

где – высота центра масс тела над произвольным нулевым уровнем, – масса тела, – ускорение свободного падения, – гравитационная постоянная, – масса планеты, – расстояние от центра планеты до центра масс тела, – коэффициент жесткости пружины, – деформация пружины.

Понятие потенциальной энергии связано с выделением особых консервативных сил. Связь между консервативной силой и потенциальной энергией задается оператором "набла", действие которого на скалярную функцию называется градиентом потенциальной энергии:

, (3.8)

Кинетическая энергия поступательного и вращательного движения

, (3.9)

где – скорость центра масс системы тел с суммарной массой ,

– момент инерции системы тел относительно оси вращения (2.5), проходящей через центр масс С этой системы,  – угловая скорость вращения вокруг этой оси (чаще всего для системы из одного вращающегося тела).

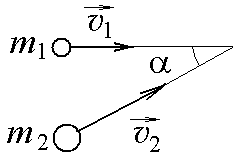3.1. Маленький пластилиновый шарик массы m₁ = 0,1 кг движется горизонтально со скоростью 1 м/с. Под углом  = 30 к направлению его движения летит второй шарик массы m₂ = 0,2 кг со скоростью 2 м/с и сталкивается с первым. Шарики слипаются и движутся под углом  к первоначальному направлению движения первого шарика. Найдите . Ответ: 0,448

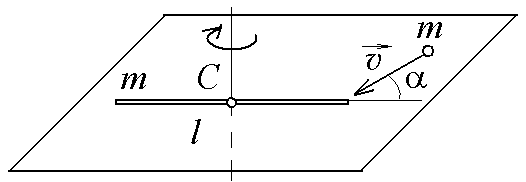3.2. На горизонтальной плоскости лежит тонкий однородный стержень массы m =0,1 кг и длины l = 1 м, который может вращаться вокруг вертикальной оси, проходящей через центр масс стержня С. Под углом  =30 к стержню в той же плоскости движется маленький пластилиновый шарик такой же массы m со скоростью = 1 м/с. Шарик прилипает к концу стержня, и система приобретает угловую скорость вращения . Найти угловую скорость вращения системы после удара. Ответ: 0,75 рад/с.

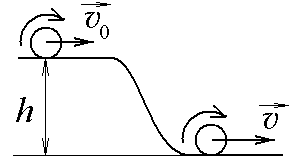3.3. Тонкий однородный диск массы m = 1 кг и радиуса R = 1 м скатывается без проскальзывания с горки высоты h = 1 м, совершая плоское движение. Начальная скорость центра масс диска равна = 1 м/с. Сопротивление воздуха пренебрежимо мало, g = 10 м/с². Найдите скорость центра масс диска , после того, как он скатится с горки. Ответ: 3,79 м/с;

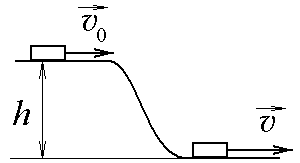3.4. Резиновая шайба массы m = 1 кг, двигаясь со скоростью = 1 м/с, соскальзывает с горки высоты h = 1 м и приобретает скорость у подножия горки. Во время движения над шайбой была совершена работа сил трения, модуль которой равен А_тр=1 Дж (g = 10 м/с²). Найдите скорость шайбы Ответ: 4,36 м/с

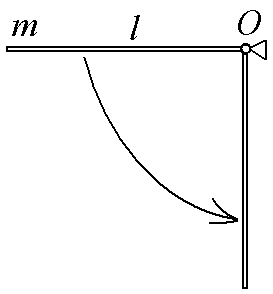3.5. Тонкий однородный стержень массы m = 1 кг и длины l = 1 м может вращаться в вертикальной плоскости вокруг горизонтальной оси, проходящей через конец стержня О. Стержень приводят в горизонтальное положение и отпускают без толчка. Сопротивление воздуха пренебрежимо мало, g = 10 м/с². В момент прохождения им положения равновесия найдите скорость нижнего конца стержня. (5,48 м/с)