
- •Розділ 1 аналіз системи автоматичного керування
- •1.1 Аналіз ланок системи і системи в цілому
- •1.2 Визначення передаточних функцій системи
- •Розділ 2 побудова амплітудно-частотних і фазових характеристик системи
- •2.1 Побудова амплітудно-частотних і фазово-частотних характеристик ланок системи
- •2.2 Побудова амплітудно-частотних і фазочастотних характеристик розімкнутої системи
- •2.3 Побудова амплітудно-частотних і фазово-частотних характеристик системи за збуренням
- •Розділ 3 побудова логарифмічних частотних характеристик системи
- •3.1 Побудова логарифмічних частотних характеристик ланок системи
- •3.2 Побудова логарифмічних частотних характеристик розімкнутої системи
- •3.3 Побудова логарифмічних частотних характеристик системи за збуренням
- •Розділ 4 дослідження системи на стійкість
- •4.1 Дослідження системи на стійкість за алгебраїчними критеріями (критерій Гурвіца)
- •Коефіцієнти дорівнюють
- •4.2 Дослідження системи на стійкість за частотними критеріями
- •4.2.1 Дослідження системи на стійкість методом d-розбиття
- •4.2.2 Дослідження системи на стійкість за допомогою критерію Михайлова
- •Висновок
- •Список використаної літератури
- •Додатки
3.2 Побудова логарифмічних частотних характеристик розімкнутої системи
При побудові результуючих частотних характеристик для групи послідовно з'єднаних ланок результуючий модуль (амплітудно-частотна характеристика розімкнутої системи) можна дістати як добуток модулів всіх ланок, а результуючу фазочастотну характеристику - як суму фазочастотних характеристик відповідних ланок. Тоді:


Рис.3.7 Логарифмічна амплітудно-частотна характеристика розімкнутої системи
3.3 Побудова логарифмічних частотних характеристик системи за збуренням
Амплітудно-частотна характеристика записується у вигляді:
![]() =
=
=![]() .
.
Логарифмічна амплітудно-частотна характеристика системи за збуренням системи:
![]()

Рис.3.8 Логарифмічні амплітудно-частотні характеристики системи за збуренням
Розділ 4 дослідження системи на стійкість
4.1 Дослідження системи на стійкість за алгебраїчними критеріями (критерій Гурвіца)
Дослідимо дану систему за критеріями Гурвіца.
Прирівняємо знаменник передаточної функції замкнутої системи до нуля і запишемо характеристичне рівняння:
![]()
Знаходимо визначник Гурвіца користуючись такими правилами:
по головній діагоналі записуємо коефіцієнт характеристичного рівняння
 ;
;місця зверху від діагоналі заповнюємо коефіцієнтами з більшим індексом, а знизу від діагоналі – з меншим індексом. При відсутності коефіцієнтів ставимо нулі.
діагональні мінори визначаємо із головного детермінанта Гурвіца викреслюванням відповідних стовпчиків і рядків.
Коефіцієнти дорівнюють
![]()
![]()
![]()
![]()
Визначаємо діагностичні мінори
![]() :
:


Система вважається стійкою у випадку якщо a0>0, a1>0, a2>0, a4>0, ∆4>0, ∆3>0, ∆2>0. Отже, система є нестійкою, бо ∆3<0, ∆2<0.
4.2 Дослідження системи на стійкість за частотними критеріями
4.2.1 Дослідження системи на стійкість методом d-розбиття
Для розв’язання поставленої задачі побудуємо межу в комплексній площині параметра k.
![]() –
характеристичне рівняння.
–
характеристичне рівняння.
Зведемо характеристичне рівняння до вигляду , коли коефіцієнт а0 дорівнює одиниці: D(p)= pn + a1pn-1+ a2 pn-2+…+ an-1 p+an=0;
Відповідно отримаємо характеристичне рівняння:
![]()
Знаходимо параметр k:
![]()
Знаходимо комплексний вираз параметра
k, використовуючи
підстановку
![]()
![]()
Виділимо дійсну А(w) і уявну В(w) складові:
![]()
Задаючи значення
![]() від
від
![]() ,
побудуємо криву D-розбиття
Практично для цього слід знайти
критичні точки, які відповідають
переходам кривої D -
розбиття через дійсну і уявну осі
комплексної площини.
,
побудуємо криву D-розбиття
Практично для цього слід знайти
критичні точки, які відповідають
переходам кривої D -
розбиття через дійсну і уявну осі
комплексної площини.
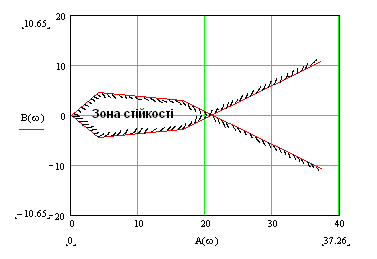
Рис.4.1 Крива d-розбиття
Із
виразу
![]() можна знайти значення
при якому
рівне нулю, що відповідає
переходу кривої D-розбиття
через горизонтальну вісь. Відповідні
значення
знайдемо із виразу:
можна знайти значення
при якому
рівне нулю, що відповідає
переходу кривої D-розбиття
через горизонтальну вісь. Відповідні
значення
знайдемо із виразу:
![]()
Звідки:
![]()
![]()
Виконані розрахунки дають змогу
встановити критичні значення параметра
kкр=22,67
з врахуванням
деякого запасу
стійкості можна виділити зону
рекомендованих значень коефіцієнта
підсилення
розімкнутої системи. Визначена за
правилом штриховки зона стійкості
знаходиться зліва від кривої D-розбиття.
Значення
k
вибирається
по
точках,
які лежать на дійсній осі
![]() ,
тому
що всі інші точки відповідають
комплексним
величинам, а коефіцієнт k
є
реальною фізичною величиною.
,
тому
що всі інші точки відповідають
комплексним
величинам, а коефіцієнт k
є
реальною фізичною величиною.
Отже, для забезпечення стійкості системи рекомендоване значення параметра k=1…20.
