3.2.3.4. Особливості реалізації алгоритмів тріангуляції.

Проблема обчислювальної стійкості є однією з основних при вирішенні більшості задач обчислювальної геометрії. Багато зовні прості алгоритми вимагають врахування численних особливих випадків, без чого алгоритм на практиці виявляється непрацездатним [3].

Обчислювальна стійкість алгоритмів тріангуляції. За зовнішньою відносною простотою описаних вище алгоритмів тріангуляції з обмеженнями в дійсності приховуються численні деталі реалізації, від яких істотно залежить стійкість роботи алгоритмів. У число таких підзадач входять: а) перевірка збігу двох заданих точок; б) перевірка взаємного розположення двох точок відносно прямої; в) перевірка колінеарності трьох заданих точок; г) перевірка взаємного розташування точки і трикутника; д) перевірка порядку обходу трьох заданих точок; е) перевірка виконання умови Делоне для двох заданих суміжних трикутників; ж) локалізація точки в тріангуляції; з) пошук точки перетину двох прямих.

У теорії всі ці завдання чудово вирішуються методами аналітичної геометрії. Однак у силу обмеженої точності обчислень операції з комп'ютерними числами не мають властивості дійсних чисел (наприклад, для них не виконуються властивість асоціативності через втрату точності в проміжних обчисленнях). Невеликими втратами точності в деяких випадках можна знехтувати, але при побудові тріангуляції цього робити не можна.

Однією з найбільш критичних до точності обчислень є операція обчислення точки перетину двох прямих, що виникає при вставці структурного ребра в тріангуляцію, що перетинає інше раніше вставлене ребро, і при дробленні ребер на частини.

В даному випадку першою проблемою є те, що обумовлена точка перетину в силу обмеженої точності обчислень, як правило, не лежить на раніше існуючому ребрі і не лежить на новому. Можливо, що ця точка лежить навіть не в суміжних з ребром трикутниках, тому в результаті розбиття старого ребра на частини утворюються нові "вивернуті" трикутники, що руйнують структуру тріангуляції. На рис. 52 наведено приклад вставки ребра АВ в тріангуляцію, що приводить до перетину з існуючим ребром в точці S (вертикальними і горизонтальними лініями розмічена дискретна координатна сітка). В результаті округлення точка перетину виявиться трохи вище реальної – у вузлі дискретної координатної сітки.

Рис. 52. Приклад можливого «вивертання» трикутників

Незважаючи на гадану екзотичність наведеного сценарію виникнення помилки, вірогідність його велика вже при спробі вкласти в тріангуляцію порядку декількох десятків взаємно перетнутих структурних ребер. Уздовж структурних ребер утворюються численні вузькі витягнуті трикутники, які і створюють зазначену критичну ситуацію.

Друга проблема в задачі пошуку точок перетину пов'язана безпосередньо з найбільш використовуваним способом обчислень. Зазвичай точка перетину (х,у) знаходиться наступним чином:

а = (x₁ - х₃) (у₄ – у₃) - (у₁ – у₃) (х₄ – х₃),

b = (х₄ – x₃) (y₂ – y₁) - (y₄ – y₃) (x₂ – x₁),

х = х₁ + а(х₂ – x₁)/b, y = y₁ + а(у₂ – y₁)/b.

Тут труднощі виникають при знаходженні точки перетину двох "майже" колінеарних відрізків. В результаті втрати точності можливе значне зміщення знайдених координат від реального значення. Крім того, через втрати точності ми можемо припускати, що відрізки перетинаються, хоча це не так. Тоді спроба обчислення їх перетину може привести до значного віддалення знайденої точки від самих відрізків (для "майже" колінеарних відрізків).

Таким чином, більшість поставлених проблем пов'язано з втратою точності внутрішніх обчислень.

Перший спосіб контролю точності за допомогою стандартних речових типів даних, запропонованих більшістю поширених мов програмування, дуже складний. Як правило, в сучасних комп'ютерах підтримуються стандарти ANSI-вистави дійсних чисел, проте навіть 10-байтовий тип extended дозволяє зберігати не більше 20 значущих цифр. У той же час, операція перевірки умови Делоне вимагає для коректних проміжних обчислень в чотири рази більшої точності. Це означає, що реально досяжна точність побудови тріангуляції Делоне становить не більше 20/4 = 5 знаків в заданні координат вихідних даних.

Інший спосіб полягає у використанні в явному вигляді обчислень з фіксованою точкою. У цьому випадку можна точно контролювати всі втрати точності.

Більш простим є перехід до цілочисельного подання координат вихідних точок. Наприклад, використовуючи звичайні 32-бітові цілі числа, можна забезпечити точність представлення в 9 значущих цифр, що є вже прийнятним в більшості ситуацій. Для реалізації алгоритму побудови тріангуляції необхідно реалізувати кілька додаткових функцій, що оперують з 32 -, 64 - і 128-бітними числами. Тоді, використовуючи цілочисельний спосіб представлення вихідних даних спільно з додатковими операціями над довгими цілими числами, можна чітко вирішити поставлені задачі.

Повернемося до проблеми пошуку точок перетину і розбиття вставлених структурних ребер на частини.

Незважаючи на те, що ми можемо виконувати обчислення за допомогою додаткових функцій практично без втрати точності, все одно точка перетину двох прямих у загальному випадку буде мати нецілі координати, які ми будемо змушені округляти, тобто в загальному випадку точка перетину двох прямих не буде лежати на цих прямих.

Таким чином, виникає необхідність модифікації всіх алгоритмів вставки структурних ліній так, щоб враховувати можливі порушення структури тріангуляції і усувати їх. Розглянемо такий узагальнений алгоритм вставки.

Узагальнений алгоритм вставки структурних ліній в тріангуляцію з обмеженнями. Нехай L - сортований по довжині список ще не вставлених структурних відрізків. Тоді узагальнений алгоритм вставки можна представити у вигляді послідовності наступних кроків.

Крок 1. Спочатку в L заносимо всі відрізки вихідних структурних ліній.

Крок 2. Послідовно в циклі витягаємо (з вилученням) з L найдовший відрізок АВ і намагаємося вкласти цей відрізок у тріангуляцію будь-яким алгоритмом вставки, описаним вище. Якщо виявляється, що вставлений відрізок перетинає деякі раніше вставлені структурні ребра (рис. 53 (а)), то їх необхідно позначити як звичайні нефіксовані ребра (рис. 53 (б)). При цьому треба знайти всі точки перетину С_і, i = , нового відрізка зі вставленими ребрами E_iF_i. Далі потрібно вставити нові точки С_і в тріангуляцію (рис. 53 (в)). Потім треба в список L помістити всі відрізки C_іC_і+1, де i = , С₀ = А, С_п+1 = В. Після цього необхідно помістити в список L всі відрізки Е_і С_і і C_іF_і i = . Якщо вставлений в список відрізок має нульову довжину, то його вставляти не треба. Цикл вставки триває, поки список L не порожній (рис. 53 (г)). Кінець алгоритму.

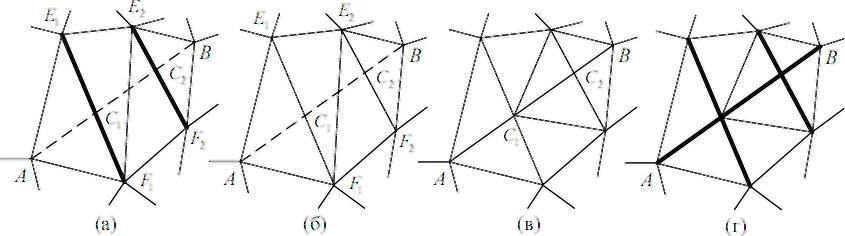
Рис. 53. Узагальнений алгоритм вставки структурних ліній в тріангуляцію з обмеженнями.

В такій реалізації алгоритму вставки на практиці досить часто виникає ситуація, коли невелика кількість вихідних структурних ліній призводить до значного розростання списку L в процесі роботи. Наприклад, задавши п'ять "майже" колінеарних відрізків як вихідних структурних ліній, можна врешті-решт отримати тисячі структурних ребер. Відбувається це внаслідок того, що кожна пара відрізків після знаходження їх перетинів утворює чотири нових відрізка,які також є "майже" колінеарними іншим відрізкам. Таке дроблення йде до тих пір, поки розміри відрізків не стануть порівнянними з розмірами одиниці координатної сітки, коли маленькі відрізки стають "зовсім не" колінеарними або розмір відрізків стає настільки малим, що його подальший поділ неможливий.

Але і на цьому мікрорівні можливі проблеми. Наприклад, нехай побудована деяка "щільна" тріангуляція, коли в кожному вузлі координатної сітки є по вузлу тріангуляції, і потрібно вкласти відрізок АВ, який перетинається з раніше вставленим структурним ребром CD (рис. 54). В результаті знайдена точка перетину АВ і CD буде округлена, наприклад, до точки - 4. У результаті в список L потраплять відрізки AC, AD і знову АВ. Так як ми витягуємо на кожному кроці зі списку найбільше ребро, то список буде нескінченно розростатися за рахунок постійної вставки ребер АС і AD.

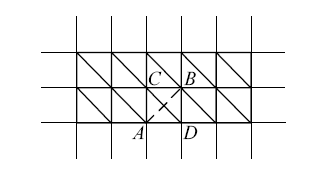
Рис. 54. Спроба вставки мікроребра

Таким чином, у цьому варіанті алгоритм вставки також не підходити для практичної роботи. Щоб уникнути перетину пар "майже" колінеарних відрізків і проблем на мікрорівні потрібні ще додаткові модифікації алгоритму.

По-перше, при вставці чергового відрізка необхідно знайти всі вузли тріангуляції, що лежать поблизу від відрізка на відстані не більше деякого ε₁. Тоді якщо такі точки знайдені, вставлений відрізок розіб'ємо цими точками на частини, які помістимо в список L.

По-друге, знайшовши точку перетину структурних ребер, перш ніж вставляти новий вузол спробуємо знайти в околиці радіусу ε₂ інший, раніше вже вставлений вузол тріангуляції.

На практиці робота алгоритму значно поліпшується вже в тих випадках, коли значення вказанних констант не менше трьох. Їх збільшення приводить до скорочення розміру списку L, але дещо збільшує час виконання додаткового пошуку точок в околицях. Найбільш прийнятними з точки зору швидкодії і якості є значення ε₁=ε₂=10.

На закінчення відзначимо, що використання цілочисельного представлення вихідних чисел дозволяє, з одного боку, явно контролювати точність обчислень, з іншого - підвищити швидкість роботи алгоритму побудови тріангуляції за рахунок відмови від речових операцій.

Проте, простий перехід від речових обчислень до цілочисельних призводить до іншого неприємного ефекту - значного зростання кількості структурних ребер в тріангуляції. Щоб уникнути цього доводиться кілька ускладнювати алгоритм, вводячи додаткові перевірки на наявність співпадаючих вузлів тріангуляції з деякою заздалегідь заданою точністю.