3.2.3.4. Алгоритми побудови тріангуляціїї з обмеженнями

Однак у багатьох випадках на структуру тріангуляції часто накладаються додаткові обмеження. Типовим прикладом є тріангуляція нутрощі деякого багатокутника.

У загальному випадку в задачі тріангуляції з обмеженнями задається безліч відрізків, з якими ребра тріангуляції не перетинаються, а тільки проходять по них. Така загальна постановка використовується в геоінформатиці при моделюванні поверхонь, коли в якості вихідних точок беруться висотні позначки на поверхні, а обмеженнями виступають так звані структурні лінії рельефа – обриви, межі водойм, хребти гір і т.д. (Рис. 43).

(а) (б) Рис. 43. Приклад тріангуляція з обмеженнями (а - вихідні дані, б-тріангуляція)

Задача побудови тріангуляції з обмеженнями також є неоднозначною, тому виникає питання вибору типу такої тріангуляції. Оскільки майже всі види тріангуляції трудомісткі і, тим самим, не ефективні для практичних реалізацій, більш кращою виявляється тріангуляція Делоне або її окремі наближення. При її використанні або додаються деякі додаткові точки в тріангуляцію (щоб виконувалася умова Делоне), або умова Делоне ігнорується вздовж вихідних відрізків-обмежень.

Розглянемо найбільш поширені алгоритми побудови тріангуляції з обмеженнями в відповідності на наступної схеми:

1. Жадібний алгоритм побудови тріангуляції.

2. Перебірний алгоритм (метод галузей і границь) побудови оптимальної тріангуляції.

3. Ланцюговий алгоритм побудови тріангуляції.

4. Ітеративні алгоритми побудови тріангуляції Делоне з обмеженнями.

4.1. «Будуй, розбиваючи»

4.2. «Видаляй і будуй»

4.3. «Перебудовуй і будуй»

3.2.3.4. Види тріангуляції з обмеженнями

Для подальшого обговорення введемо кілька означень. [1, 3, 4].

Т	Планарной тріангуляцією називається розбиття площини на М фігур, з яких одна є зовнішньої нескінченною, а решта – трикутниками
Т	Завдання побудови тріангуляції з обмеженнями. Нехай дано безлічі точок {P1,….,Pk} і відрізків {Q1,….,Ql}. Необхідно на безлічі точок {P1,….,Pk} і кінців відрізків Qi побудувати тріангуляцію таким чином, щоб всі відрізки проходили по ребрах тріангуляції. Вихідні відрізки Qi називаються структурними лініями
Т	Ребра тріангуляції з обмеженнями, за якими проходять вихідні структурні лінії, називаються структурними ребрами (фіксованими, неперебудовувані).

Серед різних видів тріангуляції з обмеженнями виділяють три основних види тріангуляції: жадібну, оптимальну і тріангуляцію Делоне з обмеженнями.

Жадібна тріангуляція. Жадібний алгоритм побудови тріангуляції з обмеженнями може бути представлений послідовністю наступних кроків.

Крок 1. Під безліч вихідних точок поміщаються кінці всіх структурних відрізків, потім генерується список всіх можливих відрізків, що з'єднують пари вихідних точок; отриманий список сортується по довжинах відрізків.

Крок 2. Виконується вставка відрізків в тріангуляцію від більш коротких до довгих. Спочатку вставляються всі структурні відрізки, а потім вставляються інші відрізки. Якщо відрізок не перетинається з іншими раніше вставленими відрізками, то він вставляється, інакше він відкидається. Кінець алгоритму.

Зауважимо, що якщо всі можливі відрізки мають різну довжину, то результат роботи цього алгоритму однозначний, інакше він залежить від порядку вставки відрізків однакової довжини.

Умовою правильної роботи жадібного алгоритму є відсутність взаємних перетинань вихідних структурних відрізків. Якщо такі є, то від них треба позбутися до початку роботи жадібного алгоритму розбивкою цих відрізків на частини.

Т	Тріангуляція з обмеженнями називається жадібною, якщо вона побудована жадібним алгоритмом

Трудомісткість наведеного алгоритму становить О(N³) щодо загальної кількості вихідних точок і відрізків. Вона складається з квадратичної кількості О(N²) всіх можливих відрізків, кожен з яких при вставці повинен бути перевірений на перетин з усіма раніше вставленими відрізками.

Даний алгоритм може бути кілька покращено за рахунок прискорення процедури перевірки вставленого відрізка на перетин з іншими. В [6] описана така процедура на основі дерева відрізків, що дозволяє виконувати одну перевірку за час О(log N) Однак ця процедура досить громіздка в описі і реалізації і тому використовується рідко. Логічно більш простим способом є переміщення всіх відрізків в R-дерево. Тоді перевірка перетину буде виконуватися в гіршому випадку за О(N) операцій, а в середньому через О(log N) операцій.

Таким чином, трудомісткість роботи жадібного алгоритму при деяких його поліпшення становить О(N²logN) без урахування попереднього етапу видалення пересічних відрізків. Якщо попередній етап приймається до уваги, то складність оцінюється як О(N⁴logN), оскільки в гіршому випадку може утворитися О(N2) менших відрізків. У зв'язку з настільки великою трудомісткістю на практиці такий алгоритм застосовується рідко.

Оптимальна тріангуляція. Дамо визначення цього виду тріангуляції.

Т	Тріангуляція з обмеженнями називається оптимальною, якщо сума довжин всіх ребер мінімальна серед усіх можливих тріангуляції з обмеженнями, побудованих на тих самих вихідних даних.

Завдання побудови оптимальної тріангуляції, очевидно, є NP-повною, тобто має складність О(е^N), а тому на практиці вона майже не застосовується.

Тим не менш, іноді виникає необхідність її побудови. Для цього використовується алгоритм повного перебору в глибину всіх можливих тріангуляції з елементами методу гілок і границь. У його основі лежить жадібний алгоритм, тому якщо перервати його роботу, то вийде деяка тріангуляція, сумарна довжина ребер якої буде гарантовано не більше, ніж у жадібної тріангуляції. Ця властивість дозволяє отримувати в умовах обмежень на час роботи алгоритму деякий прийнятне наближення.

Алгоритм повного перебору побудови оптимальної тріангуляції складається з наступних кроків.

Крок 1. Під безліч вихідних точок поміщаються кінці всіх структурних відрізків. Потім генерується список усіх можливих відрізків (r₁, r₂,...,r_m), що з'єднують пари вихідних точок; отриманий список сортується по довжинах відрізків. Виконується вставка всіх структурних відрізків в тріангуляцію і обчислюється сумарна довжина всіх ребер S в тріангуляції. Потім встановлюється мінімальна досягнута сума всіх ребер (S_max: = ∞).

Крок 2. Виконуються кроки 3 - 5 алгоритму, починаючи з першого елемента списку, тобто при к = 1 (кроки 3 - 5 по суті утворюють одну рекурсивну процедуру).

Крок 3. Виконується спроба вставки відрізка r_к в тріангуляцію. Якщо відрізок не перетинається з іншими раніше вставленими відрізками, то виконуємо наступне. Відрізок вставляється в тріангуляцію і обчислюється поточна сумарна довжина ребер S: = S + s_k, де s_k - довжина ребра r_к. Якщо S < S_max і k <M, то виконується крок А. Якщо S < S_max і k = М, то виконується крок Б.

Крок 4. Тепер відпрацьовується варіант, коли відрізок r_к не включається до тріангуляції. Для цього рекурсивно виконується крок 3 при к := к + 1.

Крок 5. Знайдена тріангуляція, що дає S = S_max, приймається за шукану і робота алгоритму завершується.

Крок А. Рекурсивно виконується крок 3 при к: = к + 1. Потім покладається к: = к - 1, S: = S - s_k і виконується повернення до точки виклику даного кроку.

Крок Б. Запам'ятовується поточна знайдена тріангуляція, покладається S = S_max і виконується повернення до точки виклику даного кроку. Кінець алгоритму.

Даний алгоритм у гіршому випадку має трудомісткість О(ε^N) проте в середньому на реальних даних він показує значно меншу трудомісткість, що дозволяє застосовувати його на відносно не великих розмірах вихідних даних.

Для побудови оптимальної тріангуляції при великій кількості вихідних даних на практиці зазвичай використовуються наближені методи [2]. Для цього в якості основи береться деяка інша тріангуляція, яка може бути побудована досить швидко (наприклад, жадібна тріангуляція або тріангуляція Делоне), а потім вона послідовно поліпшується. Поліпшення зазвичай проводиться локальною перебудовою пар сусідніх трикутників або їх небагатьох груп. Умовою вибору будь-якого перестроювання є зменшення сумарної довжини ребер.

Тріангуляція Делоне з обмеженнями. Введемо наступне визначення.

Т	Тріангуляція заданого набору точок називається тріангуляцією Делоне з обмеженнями, якщо умова Делоне виконується для будь-якої пари суміжних трикутників, які не розділяються структурними ребрами

Для побудови тріангуляції Делоне з обмеженнями можуть бути узагальнені деякі з алгоритмів побудови звичайної тріангуляції Делоне [4, 5]. Найбільш добре для такого узагальнення підходять ітеративні алгоритми тріангуляції. Алгоритми тріангуляції злиттям з цієї точки зору гірше, тому що в них не завжди можливий розподіл безлічі вихідних об'єктів на непересічні частини (наприклад заходів, коли є довгі структурні лінії, що проходять через всю тріангуляцію). Алгоритми прямої побудови тріангуляції підходять краще, але вони повинні бути модифіковані шляхом додавання в процедуру пошуку чергового сусіда Делоне додаткової операції перевірки перетину зі структурними лініями. Більшість ефективних двопрохідних алгоритмів побудови тріангуляції в даному випадку використовувать не можна, тому що вони або є непридатними алгоритмами злиття, або будують величезну кількість таких витягнутих трикутників, які майже завжди доводиться перебудовувати.

Ланцюговий алгоритм побудови тріангуляції з обмеженнями. Один з перших ефективних алгоритмів побудови тріангуляції з обмеженнями заснований на процедурі регуляризації планарного графа і тріангуляції монотонних багатокутників [3]. Трудомісткість цього алгоритму становить О(N log N), де N - кількість вихідних відрізків.

Вихідними даними для ланцюгового алгоритму є безліч непересічних відрізків на площині, які утворюють по суті планарний граф. Якщо в тріангуляцію необхідно помістити також окремі точки, то їх слід додати в тріангуляцію вже після роботи даного алгоритму (наприклад, ітеративним способом).

Ланцюговий алгоритм побудови тріангуляції з обмеженнями складається з наступних кроків.

Крок 1. З безлічі вихідних структурних відрізків формується пов'язаний планарний граф (рис. 2 (a)).

Крок 2. Виконується регуляризація графа, тобто додаються нові ребра,які не перетинають інші, так що кожна вершина графа стає суміжній, хоча і з однією вершиною вище неї і однієї нижче. Регуляризація виконується в два проходи за допомогою вертикального плоского замітання [3]. У першому проході знизу вгору послідовно знаходяться всі вершини, з яких не виходять ребра, які ведуть вгору. Наприклад, на рис. 2 (б) такою є вершина В. Проводячи горизонтальну лінію, виявляємо найближчі перетнуті нею ліворуч і праворуч ребра графа AD і EF. Потім в чотирикутнику DEHG знаходимо найнижчу вершину і проводимо в неї ребро з В. Аналогічно виконується другий прохід зверху вниз (рис. 2 (в)). В результаті роботи цього кроку кожна область планарного графа стає монотонним багатокутником.

Крок 3. Кожну область графа необхідно розбити на трикутники. Для цього можна скористатися алгоритмом неопуклого злиття двох тріангуляції (рис. 44 (г)). Кінець алгоритму.

(а) (б) (в) (г)

Рис. 44. Схема роботи ланцюгового алгоритму тріангуляції (а-вихідні відрізки, б-прохід знизу вгору регуляризації графа, в - прохід зверху вниз, г - тріангуляція монотонних багатокутників)

Недоліком ланцюгового алгоритму є те, що про форму одержуваної тріангуляції нічого заздалегідь сказати не можна. Це не оптимальна тріангуляція, не жадібна і не тріангуляція Делоне з обмеженнями. Крім того, в ланцюговому алгоритмі можуть виходити дуже довгі витягнуті трикутники.

Для поліпшення якості отриманої тріангуляції можна перевірити всі пари суміжних трикутників, не розділених структурним ребром, на виконання умови Делоне і при необхідності зробити перебудування. В результаті буде отримана тріангуляція Делоне з обмеженнями.

Ітеративний алгоритм побудови тріангуляції Делоне з обмеженнями. За основу ітеративного алгоритму побудови тріангуляції Делоне з обмеженнями може бути взятий будь-який ітеративний алгоритм побудови звичайної тріангуляції Делоне. Однак найбільш зручно використовувати алгоритм динамічного кешування (4,5), так як після закінчення його роботи буде додатково створена структура кешу, яка може бути використана для подальшої швидкої локалізації точок в тріангуляції.

Ітеративний алгоритм побудови тріангуляції Делоне з обмеженнями складається з наступних кроків.

Крок 1. Спочатку виконується побудова звичайної тріангуляції Делоне на множині всіх вихідних точок і точок, що входять до складу структурних ліній.

Крок 2. Виконується вставка відрізків структурних ліній в тріангуляцію (зауважимо, що до початку цього кроку кінці відрізків, які вставляються, вже вставлені в тріангуляцію як вузли). Кінець алгоритму.

Другий крок цього алгоритму на практиці може бути реалізований по-різному. Розглянемо різні варіанти процедури вставки відрізків.

Вставка структурних відрізків «Будуй, розбиваючи». Алгоритм вставки структурних відрізків «Будуй, розбиваючи» є найбільш простим у реалізації і стійким в роботі. У ньому необхідно, послідовно переходячи по трикутниках вздовж відрізка, що вставляється, знаходити точки його перетину з ребрами тріангуляції (рис. 45 (a)). У цих точках перетину потрібно поставити нові вузли тріангуляції, розбивши існуючі ребра і трикутники на частини (рис. 46 (б)). Після цього всі новозбудовані трикутники перевіряються на виконання умови Делоне і при необхідності перебудовуються без участі фіксованих ребер.

(а) (б)

Рис. 45. Вставка структурних відрізків «Будуй, розбиваючи»

У деяких випадках недоліком даного алгоритму вставки може бути створення великої кількості додаткових вузлів і ребер тріангуляції. У той же час в інших випадках цей недолік стає перевагою, оскільки не відбувається утворення довгих вузьких трикутників, що особливо цінується при моделюванні рельєфів.

Інша перевага цього алгоритму вставки проявляється при спробі вставки структурного відрізка в тріангуляцію, в якій серед пересічних їм ребер є фіксовані. Такі ребра, як і всі інші, просто розбиваються на дві частини.

Вставка структурних відрізків «Видаляй і будуй». В алгоритмі вставки структурних відрізків «Будуй, розбиваючи» необхідно, послідовно переходячи по трикутниках вздовж відрізка, що, вставляється, знайти всі пересічні трикутники (рис. 46 (a)) і видалити їх з тріангуляції (рис. 46 (б)). При цьому в тріангуляції утворюється дірка у вигляді деякого багатокутника. Після цього в тріангуляцію вставляється структурний відрізок, який ділив багатокутник-дірку на дві частини (ліву і праву), кожна з яких потім заповнюється трикутниками (рис. 46 (в)).

(а) (б) (в)

Рис. 46. Вставка структурних відрізків «Видаляй і будуй»

Заповнення лівої і правої частин дірки трикутниками можна виконати, проходячи уздовж її границі і аналізуючи трійки послідовних точок границі. Якщо на місці цієї трійки точок можна побудувати трикутник, то він будується і границя коротшає. Такий цикл повторюється, поки кількість точок на лівій і правій границях більше двох.

Після цього всі новозбудовані трикутники повинні бути перевірені на виконання умови Делоне і при необхідності перебудовані, не зачіпаючи фіксовані ребра.

Окремим представляється випадок, коли при вставці серед безлічі пересічних ребер знаходяться фіксовані ребра. Для уникнення такої ситуації можна заздалегідь, ще до першого кроку роботи алгоритму побудови тріангуляції Делоне з обмеженнями, знайти всі точки перетину всіх структурних відрізків і розбити цими точками відрізки на частини. Таку операцію можна виконати, наприклад, за допомогою алгоритму замітання площини [3].

Іншим варіантом обліку пересічних фіксованих ребер є наступний алгоритм. Нехай при вставці чергового структурного відрізка АВ виявлено перетин з деяким фіксованим ребром CD в точці S (рис. 47 (a)). Тоді необхідно розбити пересічне ребро CD на дві частини CS і SD, також розбивши суміжні трикутники CDE і СDF на дві частини: CSE, SDE і CSF, SDF відповідно (рис. 47 (б)). Після цього завдання вставки вихідного відрізка АВ зводиться до двох вставкам ребер АS і SB (рис. 47 (в)).

(а) (б) (в)

Рис. 47. Перетин структурного відрізка, що вставляється з раніше вставленим фіксованим ребром.

Тепер зупинимося на питанні впливу структури даних на реалізацію алгоритму вставки «Видаляй і будуй». Найбільш складною частиною є видалення трикутників, тимчасове запам'ятовування границі області віддалених трикутників і подальше її заповнення. Найпростіше це завдання виконується на структурі «Вузли, ребра і трикутники», в якій запам'ятовується список граничних ребер [4].

На структурі «Вузли, прості ребра і трикутники» [4], часто використовуваної для побудови тріангуляції з обмеженнями, ребро представляється у неявному вигляді як трикутник і номер створеного ребра, тому що при безпосередньому записі ребра посилання на суміжні трикутники не формуються.

В даному алгоритмі вставки можливі ситуації, коли при видаленні трикутників необхідно зберігати деякі створюючі їх фіксовані ребра. Наприклад, на рис. 48 (а) зображена ситуація, коли необхідно вкласти структурний відрізок АВ за умови, що поблизу знаходиться раніше вставлене фіксоване ребро KL. Після видалення всіх пересічних трикутників повинно залишитися ребро KL (рис. 48 (б)), після чого необхідно заповнити трикутниками багатокутник ABKLK ліворуч від ребра АВ (рис. 48 (в)).

(а) (б) (в)

Рис. 48. Збереження фіксованого ребра при видаленні трикутників в алгоритмі вставки «Видаляй і будуй»

Розглядаючи варіант з висячим ребром, відзначимо можливість ситуації, коли це ребро взагалі не буде пов'язано з границею області віддалених трикутників (рис. 49 (а), (б)). При цьому процедура заповнення області трикутниками, безумовно, істотно ускладнюється. За складністю сама ця задача в цілому еквівалентна задачі побудови тріангуляції Делоне з обмеженнями всередині заданого регіону.

(а) (б) (в)

Рис. 49. Фіксоване ребро, незв’язане з границею області віддалених трикутників

Для рішення такої складної ситуації потрібно тимчасово видалити заважаюче фіксоване ребро KL із тріангуляції, заповнити очищену область трикутниками, а потім повторно вставити раніше видалені фіксовані ребра (рис. 49 (в)).

Вставка структурних відрізків «Перебудовуй і будуй». Головна ідея цього алгоритму вставки полягає в спробі зменшення кількості пересічних ребер за рахунок перебудови пар сусідніх трикутників до тих пір, поки не залишиться жодного перетнутого трикутника (рис. 50 (а)-(в)), тобто вставлений структурний відрізок не стане колінеарним деякому ребру тріангуляції (рис. 50 (г)).

(а) (б) (в) (г)

Рис. 50. Проста перебудова трикутників в алгоритмі вставки структурних відрізків «Перебудовуй і будуй»

Головним недоліком цього алгоритму є можливість утворення тупикових ситуацій, коли подальша перебудова пар сусідніх трикутників не зменшує числа пересічних трикутників. Приклад такої ситуації наведено на рис. 51 (а). Для вирішення ситуацій, коли не можна виконати перебудову трикутників зі зменшенням числа перетинів, необхідно перебудовувати ті пересічні пари трикутників, у яких загальна сторона утворює максимальний кут із вставленим структурним ребром. Ця операція виконується до тих пір, поки не утворюються пари суміжних трикутників, перебудова яких не зменшить кількість перетинів ребер. На рис.51 (а) таким ребром (серед тих, у яких суміжні трикутники можна перебудувати) є АВ, тому воно і перебудовується (рис. 51 (б)). Після цього виконуються звичайні перебудови зі зменшенням перетинань (рис. 51 (в) - (з)).

Випадок, коли вставлений структурний відрізок перетинає вже раніше вставлене фіксоване ребро, обробляється так само, як і в попередньому алгоритмі вставки «Видаляй і будуй».

Трудомісткості всіх трьох розглянутих алгоритмів вставки становлять в гіршому випадку О(М²), де М - кількість вузлів в тріангуляції після завершення роботи алгоритму тріангуляції з обмеженнями. Зауважимо, що при великій кількості взаємних перетинань структурних ліній ця оцінка становить О(N⁴), де N - кількість вихідних точок і вершин вихідних структурних ліній.

(а) (б) (в) (г)

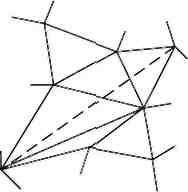
(д) (е) (ж) (з)

Рис. 51. Модифікована перебудова трикутників в алгоритмі вставки структурних відрізків «Перебудовуй і будуй»

Оцінка трудомісткості в середньому дуже сильно залежить від розподілу структурних ліній. Якщо їх кількість невелика і вони мало перетинаються між собою, то загальна оцінка трудомісткості може скласти в середньому O(N).