4.5. Умови паралельності та збіжності двох площин

Лема. Для того щоб вектор був напрямним вектором площини , необхідно й достатньо виконання такі умови:

.

Теорема 1. Для того щоб дві площини, задані рівняннями

(4.5.1)

(4.5.2)

були паралельні, необхідно й достатньо виконання такої умови:

(4.5.3)

Доведення. Необхідність. Доведіть самостійно.

Достатність. Нехай виконується умова (4.5.3). Треба довести, що площини – паралельні.

Для цього доведемо, що за умови (4.5.3) будь-який напрямний вектор однієї площини є напрямним вектором другої площини. Нехай – напрямний вектор. Тоді за лемою виконується числова рівність

. Щоб довести, що вектор – напрямний вектор другої площини, треба довести, що .

Насправді .

Отже, вектор є напрямним вектором і другої площини.

Теорема 2. Щоб дві площини, задані рівняннями (4.5.1) і (4.5.2), були збіжні, необхідно й достатньо, щоб виконувалась така умова:

(4.5.4) Із теореми 1 випливає така умова паралельності площин:

Щоб площини перетиналися, треба аби хоч один із визначників не дорівнював нулю. Цю умову можна записати в вигляді

4.6. Пряма в просторі

Пряму в просторі можна задати одним із наведених нижче способів.

I. Векторно-параметричне задання.

Задамо початкову точку і напрямний вектор (рис.10). Візьмемо довільну точку , що належить прямій.Тоді , тому ,

.

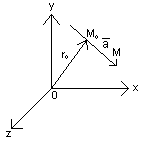
Рис. 10

II. Параметричне рівняння прямої.

Розпишемо векторно-параметричне рівняння через координати , :

.

– параметричні рівняння прямої в просторі.

III. Канонічне рівняння прямої.

Припустимо спочатку, що жодне з чисел параметричного рівняння не дорівнює нулю. Тоді можна розв’язати кожне з рівнянь відносно t.

, ,

Тому

Домовимося записувати рівняння прямої в такому ж вигляді, якщо один або навіть два із коефіцієнтів дорівнюють нулю, вимагаючи при цьому, щоб відповідні чисельники також дорівнювали нулю. Наприклад:

IV. Рівняння прямої через дві точки.

Нехай точки та належать прямій. Візьмемо за початкову точку . Тоді

.

Маємо

V) Векторне рівняння прямої:

Нехай точка належить прямій, тоді теж належить прямій ( ), тобто .

Тоді векторний добуток =

VI) Задання прямої перетином двох площин.

Отримаємо способи переходу від задання прямої одним з рівнянь I-V до VI і навпаки.

Нехай пряма задана одним із рівнянь I-V, треба знайти її рівняння VI. У цьому випадку рівняння можна подати в канонічному вигляді:

тоді

Кожне з цих рівнянь є неповне рівняння площини.

Розглянемо обернений перехід. Нехай пряма задана способом VI, треба записати її одним з рівнянь I-V. Тобто треба знайти початкову точку і напрямний вектор. Необхідно розв’язати систему . Дана система завжди сумісна, бо . Отже, система завжди сумісна і має безліч розв’язків. Тобто можна знайти початкову точку. Знайдемо напрямний вектор.

Нехай вектор – напрямний вектор даної прямої. Оскільки пряма знаходиться в першій площині, то цей вектор є напрямним вектором першої площини. Тоді за лемою виконується рівність . Так само напрямний вектор прямої є напрямним вектором другої площини, тобто .

Отже, для знаходження напрямного вектора треба розв’язати систему рівнянь:

Розв’язок цієї системи рівнянь має наступний вигляд:

.