4.2. Способи задання прямої на площині

Пряму на площині можна задати такими рівняннями

1. Загальне рівняння прямої

Означення. Загальне рівняння прямої називають повним, якщо жоден із його коефіцієнтів не дорівнює нулю, і неповним – якщо принаймні один з них дорівнює нулю.

1) Пряма, задана неповним рівнянням, має деякі особливості розташування відносно системи координат. Розглянемо всі випадки неповних рівнянь.

а) Нехай А=0, В≠0, С≠0, тоді рівняння має вигляд В у + С = 0. Тому у = 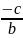– це пряма, паралельна осі Оx.

б) Нехай В = 0, А ≠ 0, С ≠ 0, тоді А х+С=0, х= , тобто пряма паралельна осі Оу.

в) С=0, тоді , тобто пряма проходить через початок системи координат.

г) А=0, С=0, тоді В≠0, з цього випливає, що В у=0, у=0, тобто пряма збігається з віссю Оx.

д) В=0, С=0, тоді А≠0, Aх=0, тобто пряма збігається з віссю Оy.

2) Нехай пряма задана повним рівнянням, тобто А≠0, В≠0, С≠0, тоді його можна записати у вигляді

де

Це рівняння прямої у відрізках (а і в – відрізки, які пряма відтинає від координатних осей).

2. Якщо в рівнянні Aх+Ву+С=0, коефіцієнт В≠0. То рівняння можна подати в вигляді

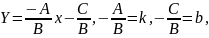так отримаємо .

У прямокутній системі координат k і b мають геометричний зміст, k – тангенс кута, який пряма утворює з віссю Оx (її додатним напрямком), k називають кутовим коефіцієнтом. b – відрізок, який пряма відтинає від осі Оy.

3. Розглянемо пряму у=kx+b, яка проходить через точку . Тоді виконується тотожність у₀=kх₀+b, із якої знайдемо , тому рівняння у₀=kх₀+b набуває вигляду .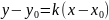

4. Геометрично пряму можна задати напрямним вектором і початковою точкою.

Означення. Напрямним вектором прямої називають ненульовий вектор, колінеарний деякому ненульовому вектору, розташованому на прямій.

Означення. Початковою точкою прямої називають будь-яку, але фіксовану точку на прямій.

Нехай задано початкову точку і напрямний вектор . Нехай точка має радіус-вектор .

Візьмемо будь-яку точку М, що має радіус-вектор 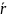. Із векторної алгебри відомо 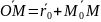_, , тоді , тобто Це рівняння називають векторно-параметричним рівнянням.

5. З векторно-параметричного рівняння прямої можна отримати параметричні рівняння прямої Для цього задамо координати точки і вектора : , . Нехай точка М має координати (х,у).

Тоді , , 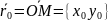а з попереднього рівняння випливає 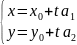– параметричне рівняння прямої.

6. З параметричних рівнянь можна отримати канонічне рівняння прямої. Припустимо спочатку, що , , тоді

тобто 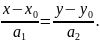Це канонічне рівняння прямої.

Домовимось записувати рівняння прямої в такому самому вигляді навіть тоді, коли 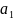або , вважаючи, що відповідний чисельник також дорівнює нулю.

0

7. Із канонічного рівняння можна отримати рівняння прямої через дві точки. Нехай задано дві точки,що належать прямій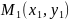 , 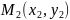. Тоді одну з точок візьмемо за початкову, а за напрямний вектор візьмемо вектор і підставимо у канонічне рівняння:

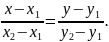
Наведене рівняння називають рівнянням через дві точки.

8. Векторне рівняння. Існують два різновиди векторних рівнянь:

1 (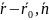 )=0, де , – радіус-вектор початкової точки;

2 [ ]= ; – напрямний вектор прямої.

9. Нормоване рівняння прямої

Означення. Нормованим рівнянням прямої називають рівняння

( )=0, у якому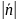 =1.

Для того щоб з векторного рівняння отримати нормоване рівняння треба помножити обидві його частини на число .

, .

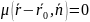Переходячи к координатному запису одержимо загальне рівняння Ax+By+C=0, . Припустимо, що система координат прямокутна, тоді , . Отримаємо координатний запис нормованого рівняння:

Щоб дане рівняння мало геометричний зміст домовимось обирати знак нормувального множника протилежним знаку вільного члена.

Нормоване рівняння можна також записати у вигляді

.

Для з’ясування геометричного змісту нормованого рівняння введемо поняття відхилення точки від прямої

Означення. Відхиленням точки М від прямої називають число, що дорівнює відстані d від точки М до прямої, якщо М та О (О – початок системи координат) знаходяться в різних півплощинах відносно прямої і дорівнює числу (–d), якщо точки М і О знаходяться в одній півплощині.

Теорема. Відхилення точки від прямої дорівнює результату підстановки координат даної точки в ліву частину нормованого рівняння прямої.

Доведіть теорему самостійно.