2.3. Перетворення координат точки площини при зміні прямокутної системи координат

У разі переході від однієї прямокутної системи координат до іншої мають місце два випадки, що геометрично різні, а формально-алгебраїчно однакові:

1) Одну систему координат можна отримати з іншої поворотом на кут (рис. 4).

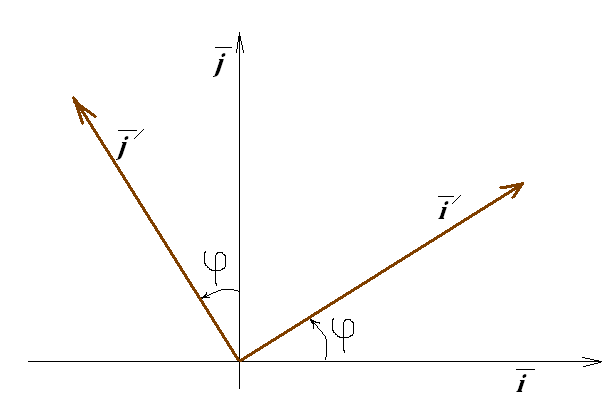
Рис. 4

2) Одну систему координат можна отримати з іншої за рахунок двох перетворень (рис. 5):

а) повороту на кут ;

б)дзеркального відображення.

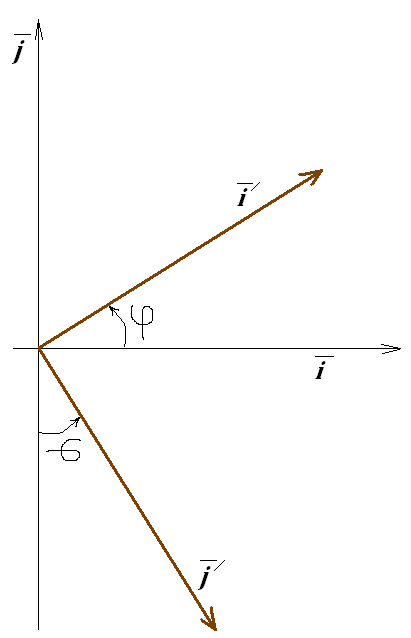
Рис. 5

1) Нехай у першій системі координат точка М має координати (х,у) у другій . Раніше було встановлено, що:

,

, де С=( ) – матриця переходу.

Знайдемо матрицю переходу:

,

.

За теоремою про геометричний зміст декартових прямокутних координат маємо:

c₁₁ = пр_ii¢= ½i¢½cosj= cosj

c₂₁ = пр_ji¢ = ½i¢½cos(90° - j) = ½i¢½sinj = sinj,

c₁₂ = пр_ij¢ = ½j¢½cos(90° + j) = -½i¢½sinj = - sinj,

c₂₂ = пр_jj¢ = ½j¢½cosj = cosj.

Тоді .

Отже, формули перетворення координат при повороті системи координат на кут мають такий вигляд:

,

2) Якщо провести аналогічні розрахунки, одержимо

,

.

3. Лінії і поверхні

3.1. Поняття рівняння лінії, рівняння поверхні

Розглянемо афінну систему координат.

Означення 1. Рівність

f(x,y)=0 (3.1.1)

називають рівнянням лінії L, якщо справджуються дві умови:

1)координати (х,у) будь-якої точки М, що належить лінії L, задовольняють рівність (3.1.1);

2) координати(х,у) будь-якої точки М, що не належить лінії L, не задовольняють рівність (3.1.1).

Розглянемо в просторі систему координат і поверхню S.

Означення 2. Рівність

f(x,y,z)=0 (3.1.2)

називають рівнянням поверхні S, якщо виконуються такі умови:

1)координати (х,у,z) будь-якої точки М, що належить поверхні S, задовольняють рівність (3.1.2);

2) координати (х,у,z) будь-якої точки М, що не належить поверхні S, не задовольняють рівність (3.1.2).

Наприклад:

.

Якщо розглянути дане рівняння на площині, то у відповідній системі координат воно являє собою рівняння лінії, а саме рівняння кола з радіусом 1 та центром у початку координат.

Якщо ж розглядати рівняння у просторі, отримаємо

.

Це циліндрична поверхня з твірною, паралельною осі Оz.

Лінію в просторі можна задати перетином двох поверхонь, тобто такою систему:

3.2. Параметричні рівняння лінії та поверхні

Лінію на площині та в просторі можна розглядати як слід рухомої точки. Тоді координати точки є функції часу, на площині:

(3.2.1)

та просторі:

(3.2.1^/)

Означення. Рівності (3.2.1) і ((3.2.1^/)) називають параметричними рівняннями лінії L на площині (у просторі), якщо виконуються дві умови:

1) для будь-якої точки М*(х*,y*) ( (x*,y*,z*) у просторі), що належить L, існує таке значення параметра , що

(3.2.2^/)

2) для будь-якої точки М(х,y) (М(x,y,z)), що не належить L, не існує таке значення параметра t, єдине для кожного з рівнянь.

Означення. Рівності

називають параметричними рівняннями поверхні S, якщо виконуються дві умови:

1) для будь-якої точки (х*,y*,z*), що належить S, існує пара значень параметрів таких, що

,

2) для будь-якої точки , що не належить S, такої пари параметрів, єдиної для всіх трьох рівностей, не існує.